汽车防撞毫米波雷达系统参数优化设计
周 刚,吴 杰
(河南工业大学电气工程学院,郑州 450007)
1 引 言
调频连续波(FMCW)雷达具有很高的距离分辨率,采用一定的调制方式可以同时进行距离和速度的测量。随着高频器件和单片微波集成电路(MMIC)的出现和应用,调频连续波(FMCW)雷达的性能有了很大的提高,成本不断下降;其外形尺寸可以做得很小,适合在汽车上安装,是目前汽车防撞雷达研究的主要方向[1]。
德国无线电通信研究所研制了一种用于装备标准大众Passat小汽车的调频连续波防撞雷达。该系统主要参数最大作用距离为150 m,距离分辨率为1 m,相对速度分辨率为2.5km/h。英国研制的汽车防撞雷达的主要参数如下:工作频率为 76~77GHz,体制FMCW,作用距离为100 m,距离精度为0.5 m,相对速度为160km/h,速度精度为1.5km/h,扫描速率为20 Hz[1]。以上防撞雷达具有较高的分辨率,但硬件成本高。本文拟研究防撞雷达工作参数与测量要求间的关系,改进信号处理算法,进而进行工作参数优化设计,降低系统硬件成本。
2 雷达系统工作原理
图1所示的线性调频连续波(LFMCW)对称三角波调制体制雷达可实现对运动目标距离和速度的测量,图中T为发射信号调频周期,f0为发射信号中心频率,B为发射信号调频带宽,fT为发射信号频率,fR为静止目标回波信号频率,fRD为运动目标回波信号频率。
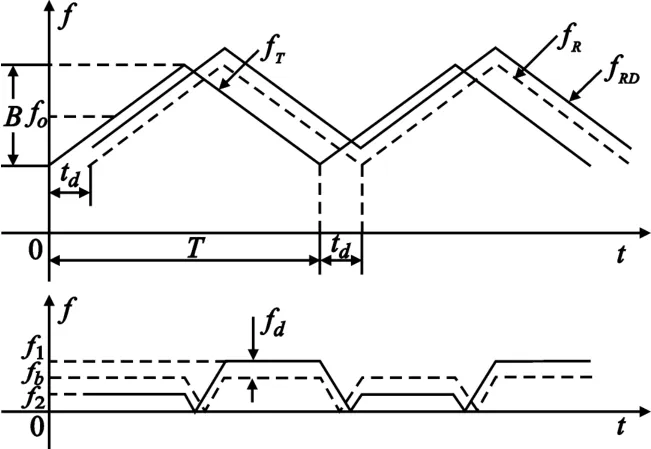
图1 线性调频连续波信号频率Fig.1 FMCW signal frequency
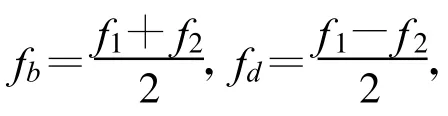
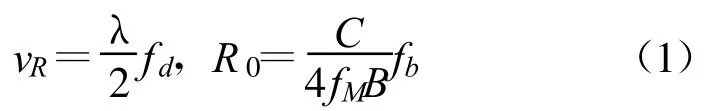
式中,C为光速。
3 雷达前端参数制定
3.1 汽车防撞测量指标
基于前车匀速行驶状态下的安全距离和相对速度关系如式(2)所示[2]:
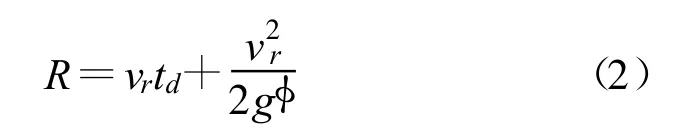
式中,R为安全距离(m),vr为两车相对速度(m/s),td为制动迟滞时间(取1.5 s), 为附着系数(取0.65)[3],g为重力加速度(取 9.8 m/s2)。基于式(2)的计算结果如表1所示(高速公路车辆速度要求低于120km/h,即33.33 m/s)。
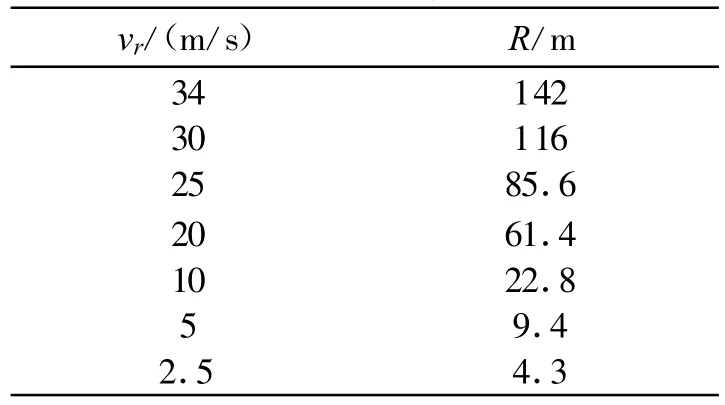
表1 相对速度和安全距离Table 1 Relative velocity and distance
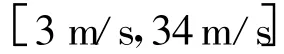
文献[1]表明汽车防撞测量中距离分辨率通常在0.2~1 m之间,速度分辨率在1~2.5km/h之间,所以制定距离分辨率为ΔR=0.5 m,速度分辨率Δv=1.8km/h(0.5 m/s)。
3.2 工作参数制定
汽车防撞雷达要求尺寸较小,为了用小尺寸天线获得足够窄的波束,雷达前端应采用尽量高的工作频率 f0,普遍采用的毫米波频率有24GHz、35GHz、77GHz、90GHz等[1]。由于多普勒频率 fd与工作频率f0成正比,fd与fb存在耦合关系,选取f0时需考虑fd的范围以及速度分辨率Δ v对应的频域频率fdΔ。常用频率f0对应的fd范围如表2所示。
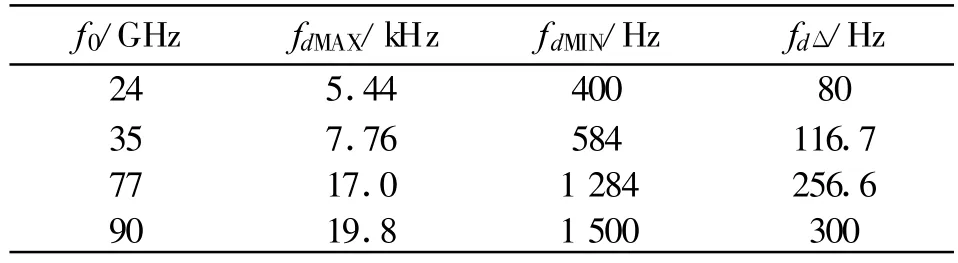
表2 fd与常用中心频率f0数值关系Table 2 Relation between fdand f0
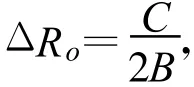
由于fd与fb的耦合关系,而fb与fM直接相关,在选定工作频率 f0时需考虑调制频率 fM。表3给出了fb与备选的fM间的数值关系(距离分辨率ΔR对应频域频率为fbΔ)。
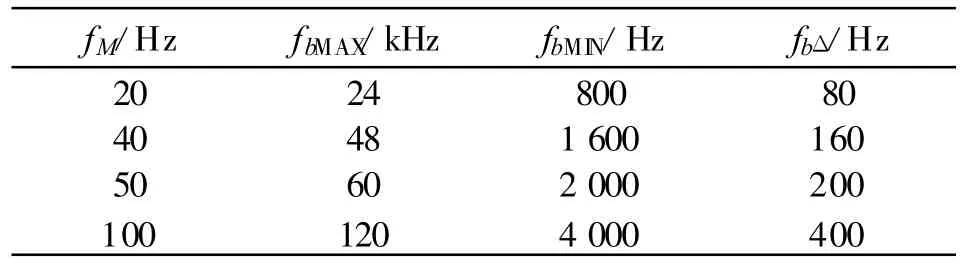
表3 fb与调频频率fM的关系Table 3 Relation between fband fM
由于fd与速度vr成正比,fb与距离R成正比,距离测量动态范围大于速度测量动态范围,理论上只要满足fbMIN>fdMIN,在f0和fM确定的情况下,随着距离和速度的增加,fb不会被fd淹没。实际应用中,考虑低速较近距离时对突然闯入物的有效预警,取 fbMIN≥3fdMIN。
基于以上讨论,参考表2和表3数据,选定雷达前端中心频率f0=24GHz,调频频率fM=40 Hz,调频周期 T=0.025 s。
4 信号处理参数设置
由以上工作参数确定的多普勒频率 fd的范围为(0.4kHz,5.44kHz),距离产生的差拍信号中心频率fb范围为(1.6kHz,48kHz),对应的差拍信号最高频率 fbmax=53.44kHz。考虑到实际系统的非理想特性,工程应用一般选取采样频率为信号最高频率的3~5倍,所以选定采样频率为200kHz。
4.1 信号处理技术指标
进行时频分析时,要求距离分辨率ΔR和速度分辨率Δ v在频域可分辨。采样率一定情况下,采用FFT进行频谱分析时,FFT的长度决定了频率分辨率,从而决定了测量分辨率。FFT点数NFFT的选取需考虑测量范围和分辨率要求。在满足分辨率要求下,考虑系统实时性要求,希望NFFT适当小些,而且是2或4的整数次幂。
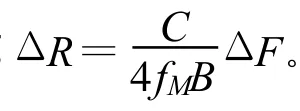
相对速度的分辨率取决于多普勒频率的测量。由表2可知速度分辨率Δv对应的多普勒频率fdΔ=80 Hz,如果 fdΔ<ΔF,则在对正负调频期间差拍信号进行频谱分析求取 f1和 f2时,fdΔ将无法分辨,这样造成距离速度模糊:一方面得不到准确的多普勒频率值,速度测量误差大或者无法测速;另一方面将造成距离速度耦合使测距误差加大,所以要得到目标不模糊速度信息,就要求FFT频谱分析时多普勒频率 fdΔ在频域可分辨,频率分辨率 ΔF 基于以上讨论,要求ΔF=fs/N<80 Hz,若采用直接 FFT方法进行频谱分析,则FFT点数N≥2500,即 N ≥4096。 正负调频期间有效采样时间小于0.0125 s(T/2),采样数据个数N<2500<4096,尽管通过补零或插值方法可以实现4096点FFT,但4096点的FFT运算量很大,要保证系统的实时性,硬件成本高,而较少点数的FFT不能满足频率分辨率要求。线性调频Z变换(CZT)是提高频率分辨率的频谱细化方法之一[5,6]。 Chrip-Z变换是由傅里叶变换导出的一种频谱分析方法,等价于离散时间傅里叶变换在部分频带上的频谱等间隔取样,可对信号带宽中的部分频带进行高分辨率的频谱细化分析。采用FFT和CZT联合算法进行频谱分析在同等分辨率下可明显降低运算量。首先通过较少点数的FFT进行差拍信号粗略频谱估计,然后再利用CZT方法对该位置附近的频谱局部细化。M点x(n)的Chrip Z变换为 式中,k=0,1,2,… ,M-1;A=A0ejθ0,W=W0e-jφ0 。 CZT算法关键是确定分析频段的起始点及采样间隔,即 θ0和 φ0。通过 N点的FFT得到频谱谱峰位置为Kmax(Kmax 细化后频域采样间隔ΔF=2fs/MN,达到MN/2点FFT的分辨率,所以要求N·M≥8192,则联合算法频率分辨率ΔF≤48.8 Hz<80 Hz。 相同频率分辨率下,对于N·M点FFT,若直接采用FFT的方法,其运算量为0.5(N·M)lb(N·M);若采用联合FFT和CZT算法,则联合算法的总运算量为0.5N lb N+1.5(N+M)lb(N+M)[5]。 汽车防撞系统是低速较近距离的测量,速度分辨率和距离分辨率要求较高,对应较高的频率分辨率(频率间隔较小)。防撞系统扫描周期短,信号处理中,若采用直接FFT方法,其运算量很大,很难保证系统实时性要求;或者增加系统硬件配置以提高处理速度,这无疑提高了硬件成本。而相同的分辨率,联合算法的运算量远小于直接FFT的运算量,满足系统实时性要求。所以相同运算量,采用联合算法可大幅度提高系统的频率分辨率。 影响FFT点数与CZT点数选取的主要因素是有效采样期间采样点数和噪声。FFT点数太低,采样数据错误的偶然性增加,可能影响频谱范围选择的正确性,进而影响测频正确性[6]。FFT法受噪声影响较小,其频率估计误差比无噪声情况下略大一点,而FFT-CZT法的频率估计误差受噪声影响较大,所以联合算法更适用于高信噪比的信号[1]。在满足系统实时要求前提下选择大点数FFT和小点数CZT进行频谱分析。 取N=256,M=40,则联合算法频域分辨率ΔF=39.1 Hz<80 Hz,联合算法所需时间约为直接FFT的1/16,能够满足实时性和分辨率要求。 LFMCW雷达应用于汽车防撞,针对系统间各个参数相互影响,在进行系统设计时应全面考虑各个参数间的制约关系。本文重点讨论了与时域分辨率和频域分辨率相关的参数,根据信号处理过程制定了具体的工作参数。本文研究的参数设计方法已应用于汽车防撞雷达系统设计中,其方法过程也可作为LFMCW雷达其它应用领域或者信号处理的参考。本文的研究考虑路况较简单,对复杂路况、多目标背景下,需进一步研究虚警产生和工作参数间的关系,以及中频信号噪声产生的原因,研究通过设置合适的工作参数最大程度剔除虚警等问题。 [1] 郑兴林.毫米波汽车防撞雷达信号处理关键技术研究[D].长沙:国防科学技术大学,2007.ZHENG Xing-lin.Research on Key Technique of Automobile Anti-collision Millimeter Wave Radar signal Processing[D].Changsha:National University of Defense Technology,2007.(in Chinese) [2] 唐阳山,江振伟,白艳,等.汽车防碰撞安全距离模型及仿真研究[J].辽宁工业大学学报(自然科学版),2008,38(5):324-326.T ANG Yang-shan,JIANG Zhen-wei,BAI Yan,et al.Model of Vehicle Safety Distance for Collision Avoidance and Simulation Study[J].Journal of Liaoning University of Technology(Natural Science Edition),2008,38(5):324-326.(in Chinese) [3] 杨翠萍,官慧峰.高速公路汽车防撞系统的安全行车距离研究[J].自动化仪表,2008,29(9):19-21.YANG Cui-ping,GUAN Hui-feng.Research on Safe Distance between Vehicles for Freeway Anti-collision System[J].Process Automation Instrumentation,2008,29(9):19-21.(in Chinese) [4] 梁品,陈照章,于敬泉.基于DSP的汽车防撞雷达及其信号处理[J].微电子学,2007,37(5):628-631.LIANG Pin,CHEN Zhao-zhang,YU Jing-quan.Design of Anti-collision Radar for Automobiles Based on DSP and Its Signal Processing[J].Microelectronics,2007,37(5):628-631.(in Chinese) [5] 肖慧,胡卫东,郁文贤.基于DPT-CZT处理的LFMCW雷达参数估计[J].现代雷达,2008,30(11):48-50.XIAO Hui,HU Wei-dong,YU Wen-xian.parameter Estimation Based on DPT-CZT Processing in LFMCW Radar[J].Modern Radar,2008,30(11):48-50.(in Chinese) [6] 齐国清.几种基于FFT的频率估计方法精度分析[J].振动工程学报,2006,19(1):86-89.QI Guo-qing.Accuracy analysis and comparison of some FFT-based frequency estimation[J].Journal of Vibration Engineering,2006,19(1):86-92.(in Chinese)4.2 技术参数的优化实现

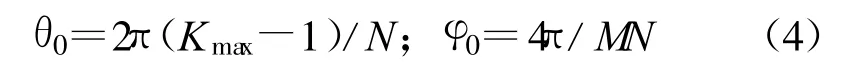
5 结束语

