GPS电离层延迟误差修正中二阶项角度的分析
张成义,赵 威,詹 煜,杨星星
(南京信息工程大学数理学院,南京 210044)
1 引 言
电离层的延迟误差直接影响到GPS的准确定位,因此,延迟误差的精度备受关注。对延迟误差的修正,不同的用户有不同的选择。一般情况下,单频接收机用户采用模型改正法进行误差修正,常见的模型有Klobuchar模型和 IRI模型,其中Klobuchar模型被GPS系统的广播星历所采用,双频接收机用户采用双频改正法进行误差修正,这种方法可将电离层延迟误差修正到厘米级精度,使电离层延迟引入的距离误差修正至90%以上。但是,双频改正技术仅能消除电离层延迟误差中一阶项的影响,而在军事及地震灾害预测等相关领域,由于对精度的要求明显提高,仅消除电离层延迟误差中的一阶项往往不能满足要求。在这种情况下,研究误差中高阶项的影响对提高观测精度、应用水平尤为重要。
本文旨在使延迟误差从厘米级水平提高到毫米乃至更高的水平,探讨对误差项中二阶项进行修正的方法。研究表明,采用3个频率可以对二阶项进行修正,该方法的实质是不同测量频率的线性组合,这种组合可使延迟误差从厘米级提高到毫米级。通过对二阶项的分析可以看到,信号传播方向与地磁场方向的临界夹角θ对误差修正会产生重要影响,本文的第4部分给出了取得毫米级误差要求时θ的取值。
2 电离层延迟误差
离地面约70~1000km的大气层称为电离层,电离层中的大气分子在太阳光的照射下会分解成大气电离子和电子。当电磁波穿过充满电子的电离层时,它的传播速度和方向会发生改变[1]。研究表明,在电离层内,由传播路径弯曲造成的测距误差通常比电磁波传播速度变化造成的测距误差要小几个量级,只有在卫星高度角较小时,前者的影响才大于后者。因此在定位测量中,只要卫星高度角不很低,一般可忽略路径弯曲效应。由于传播速度的改变,电磁波经过电离层的时间将改变,然而我们在计算电磁波穿过电离层这一部分距离的时候仍是用光速与经过电离层时间的乘积作为测距结果。这样因传播速度的改变而测得的值与真实值的差异就叫做电离层延迟误差。
电离层中单一频率的电磁波信号其相速度vp与相折射率nP有如下关系:

式中,c为真空中光速,相位传播折射率np可表示为[2]
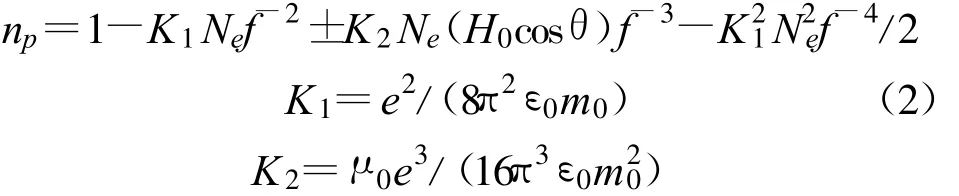
式中,Ne为电子密度,即单位体积内自由电子的个数,e为电子电量,ε0为真空中的介电常数,m0为电子的静止质量,θ为电磁波传播方向与地磁场方向的夹角,f为入射电磁波的频率。当电磁波传播信号为右旋极化波时,K2前取负号;反之,当信号为左旋极化波时,K2前取正号,本文中取负号进行分析。
当电磁波穿过电离层时,若 s为电磁波穿过电磁层的路径,则由折射率变化引起的传播路径距离误差为[4]
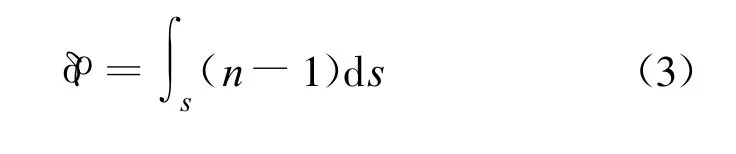
在电磁场理论中,关于群折射率ng和相折射率np有如下关系[1]:
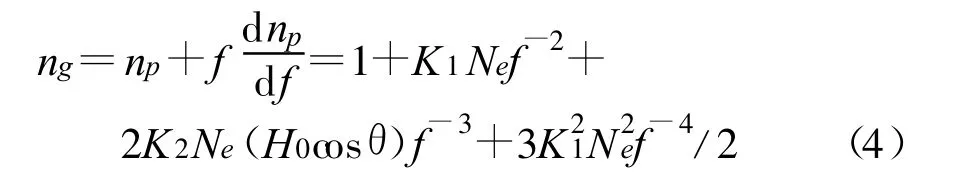
所以由相折射率变化和群折射率变化引起的电离层延迟误差分别为
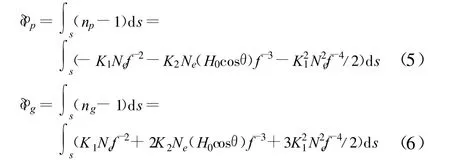
GPS信号作为电磁波的一种,由折射率变化造成的电离层延迟误差一般为几米。当太阳黑子活动剧烈的时候,随着电离层中电子密度Ne的增加,电离层延迟误差也将增大,其值可达十几米甚至几十米,因而GPS通常不能忽略电离层延迟对GPS测量和定位的影响。
为方便研究,通常把式(5)和式(6)简写成:
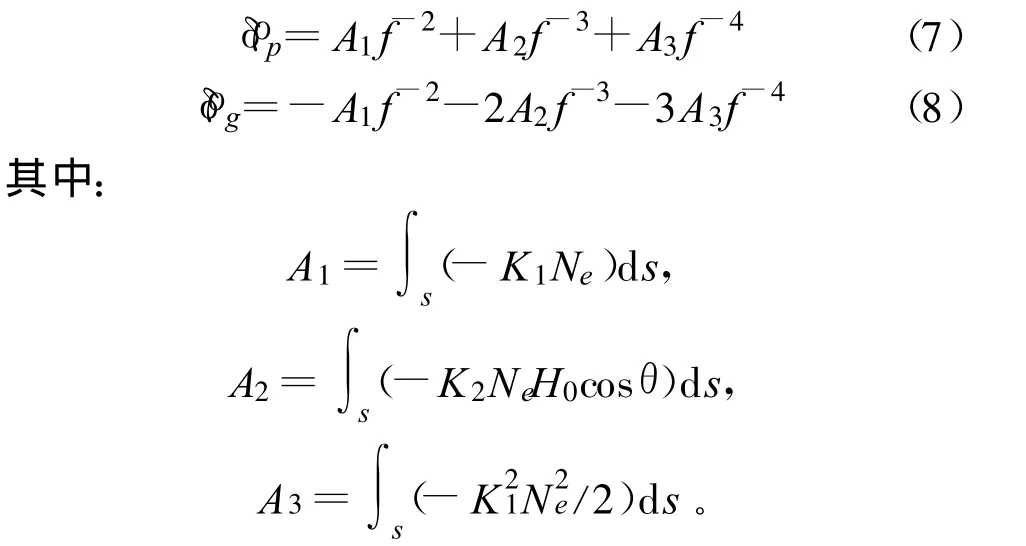
对于式(7)和式(8)中一阶项的修正采用的是双频修正法,该方法可以将误差修正90%以上。对于二阶项的修正,随着第三个频率的出现,运用3个频率对电离层延迟误差二阶项的修正已成可能。
3 消除电离层延迟误差二阶项的三频修正
随着GPS现代化和Galileo计划的开展,美国在2009年3月24日成功发射了ⅡR(20)-M型GPS卫星,该卫星在2009年4月10日实现了载波L5的发播,由于民用L5的出现,增加了一个观测量,加上原有的 L1、L2(L1、L2、L53个载波对应的频率分别为f1、f2、f3),运用3个频率对电离层延迟误差二阶项的修正成为可能。
GPS接收机从卫星信号中可获得两种基本测量值,一种是伪距测量值,另一种是载波相位测量值。伪距测量值是通过接收机获取C/A码,该码相位值反映着卫星播发该信号的卫星时间,通过与接收机时间相比较,可以计算出接收机距卫星的距离。C/A码以群速度传播,因此可通过群折射率的变化引起的电离层延迟误差来修正伪距测量值。载波相位测量时首先要获取载波在接收机与卫星之间的相位差,然后通过计算出周整模糊度N,以此来确定接收机距卫星的距离。载波以相速度传播,因此可通过相折射率的变化引起的电离层延迟误差来修正载波相位测量值。
首先分析伪距观测中二阶项的修正:
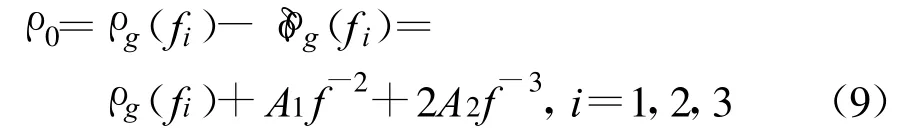
式中,ρ0表示星站间的几何距离,ρg(f1)、ρg(f2)、ρg(f3)分别为在伪距测量中导航频率 f1、f2、f3同步观测的观测站距卫星的距离,为方便计算,用 ρ1、ρ2、ρ3代替。
f1=1575.42MHz,f2=1227.60MHz,f3=1176.45MHz是GPS导航信号中3个频率,代入式(9)中求解2A2。参考文献[3]的计算结果:
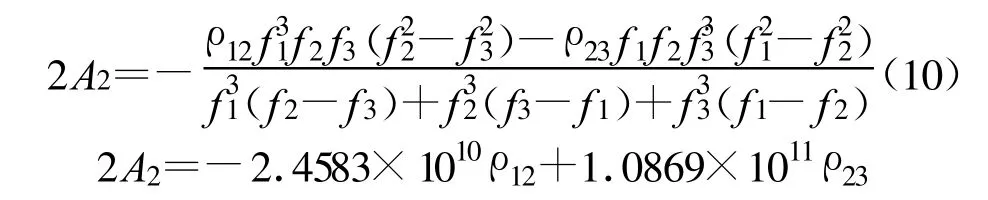
从而可求得三频伪距观测值二阶项的电离层延迟距离修正值,不同频率求得结果对应如下:

式中 ,ρ12=ρ1-ρ2,ρ23=ρ2-ρ3。
载波相位观测中二阶项的修正方法同伪距观测:
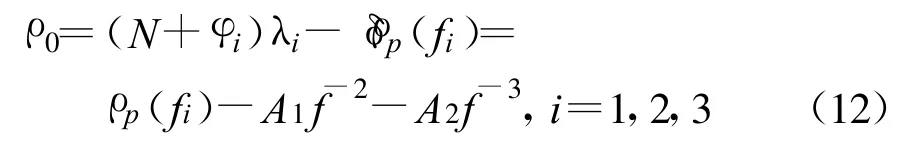
式中,ρ0表示星站间的几何距离;N是未知的整数,通常称为周整模糊度;φ是载波信号从卫星端到接收机端的相位变化;λ是波长,所以(N+φ)λ是载波相位观测中测得的接收机距卫星的距离。ρp(f1)、ρp(f2)、ρp(f3)分别为在载波相位测量中导航频率f1、f2、f3同步观测的观测站距卫星的距离,为方便计算用 p1、p2、p3代替。
对式(12)进行计算,参考文献[3]的计算结果:
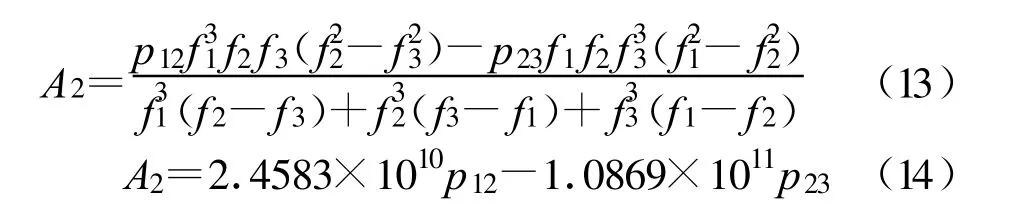
从而可求得载波相位观测值二阶项的电离层延迟距离修正值,不同频率求得结果对应如下:
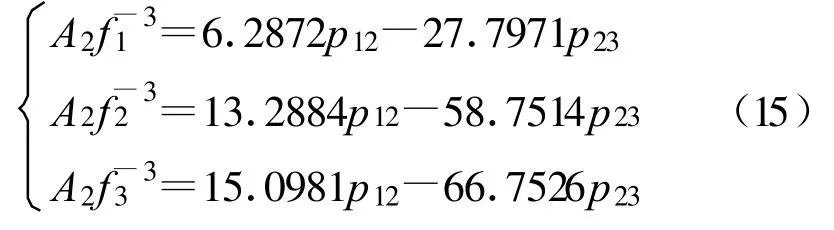
式中,p12=p1-p2,p23=p2-p3。
式(11)和式(15)分别为GPS三频伪距观测值和载波相位观测值二阶项的电离层延迟距离修正。
4 二阶项中θ角度的影响
用三频消除电离层延迟误差中二阶项的影响,伪距和载波相位延迟误差修正中事实上分别是用ρ1、ρ2、ρ3的线性组合和 p1、p2、p3的线性组合。这种组合虽然能消除电离层二阶项的误差,但是却出现组合测量噪声量。
分析二阶项 A2f-3,f为信号频率,A2=,K2为常数。故若要精确求解二阶项,只需确定的值。令 NTEC=,其物理意义是:在信号传播路径上的、横截面为1 m2的这样一个管状通道空间所包含的电子数总量。由于H0cosθ变化缓慢,文献[6]中的处理方法是将电离层中的信号传播路径分成n 等份,求出各端点上的 H0和 θ,并计算各端点的H0cosθ,将所得的结果做平均处理得到,然后就可将平均值从积分号外提出来,将公式简化为
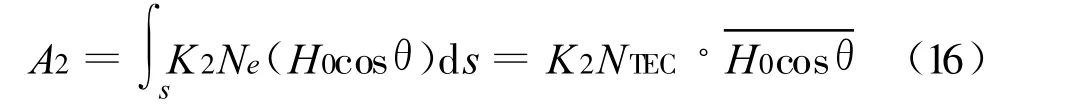
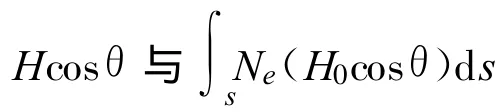
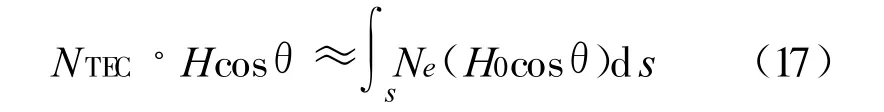
在本文中,主要分析 θ角在二阶项中影响,因此可将特定高度的H看成已知数,并在此基础上分别考虑最大电子含量时和一般电子含量时两种情况。考虑 H0=B/μ0,其中B为地球磁感应强度,大小基本稳定,取值参考国际地磁场模型IGRF10,其量级一般在10-5T,不超过10-4T;地表处B值大小一般在2.5×10-5~6×10-5T,其大小变化为从赤道向两极逐渐增大。本文取B=5×10-5T,研究 θ角的变化对二阶项的影响。
最大太阳活动周期的时候NTEC=4.55×1018,通常的情况 NTEC=1.38×1018,将值分别代入到K2NTEC·Hcosθ中,令 A2max对应最大太阳活动周期时候的电子含量,A2对应通常情况的电子含量,经过计算有:
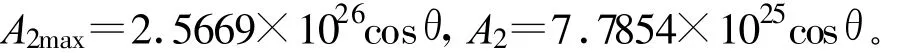
分析θ角对二阶项A2f-3影响,取6组不同的角度,其计算结果如表1所示。
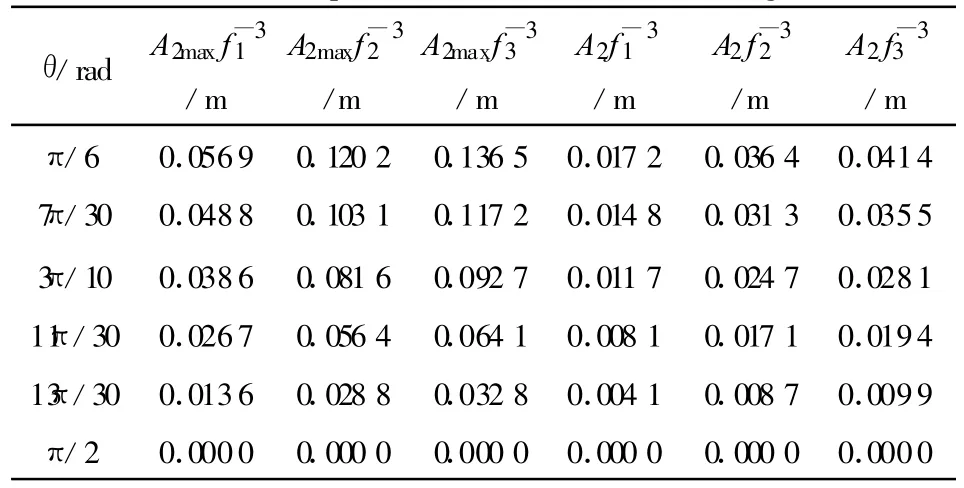
表1 不同的角度解算结果Table 1 Computational result of different angles
表1取6组不同角度分别计算了最大太阳活动周期时候的电子含量和通常情况下的电子含量所对应的二阶项延迟值。从表中可以看出,采用3个频率所能达到的精度在上述两种情况下均可达到厘米级。在通常情况下接近垂直的方向上3个频率可以达到毫米级的修正度。对二阶项的修正一般情况下要求达到毫米级精度,这样对 θ角度的选取就很有必要。
对表中的数据进行拟合可得到图1所示的曲线。从图1中可以看出不同频率随角度θ变化时对应的二阶项修正值的变化情况。
对图形进行曲线拟合,则可利用拟合的曲线方程计算出不同的误差值所对应的角度。
分析图1(b),令x、y分别表示其横坐标和纵坐标。曲线是用三阶多项式拟合而成,则可求得3个频率对应的曲线方程分别为
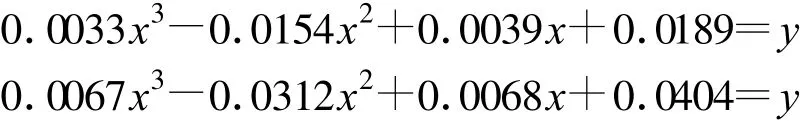
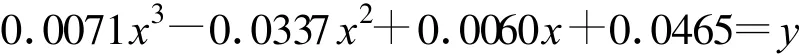
从图1(b)中可知,二阶项修正至毫米级精度只有在电磁波传播方向与地磁场方向的夹角 θ大于某一特定值时才会实现。
在图 1(b)中,a、b、c三点对应的纵坐标是0.01,即横坐标分别是3个频率的二阶项修正值要达到毫米级精度所需的最小夹角。通过计算得到a、b、c三点x对应的横坐标值分别是1.0407、1.3304、1.3641。
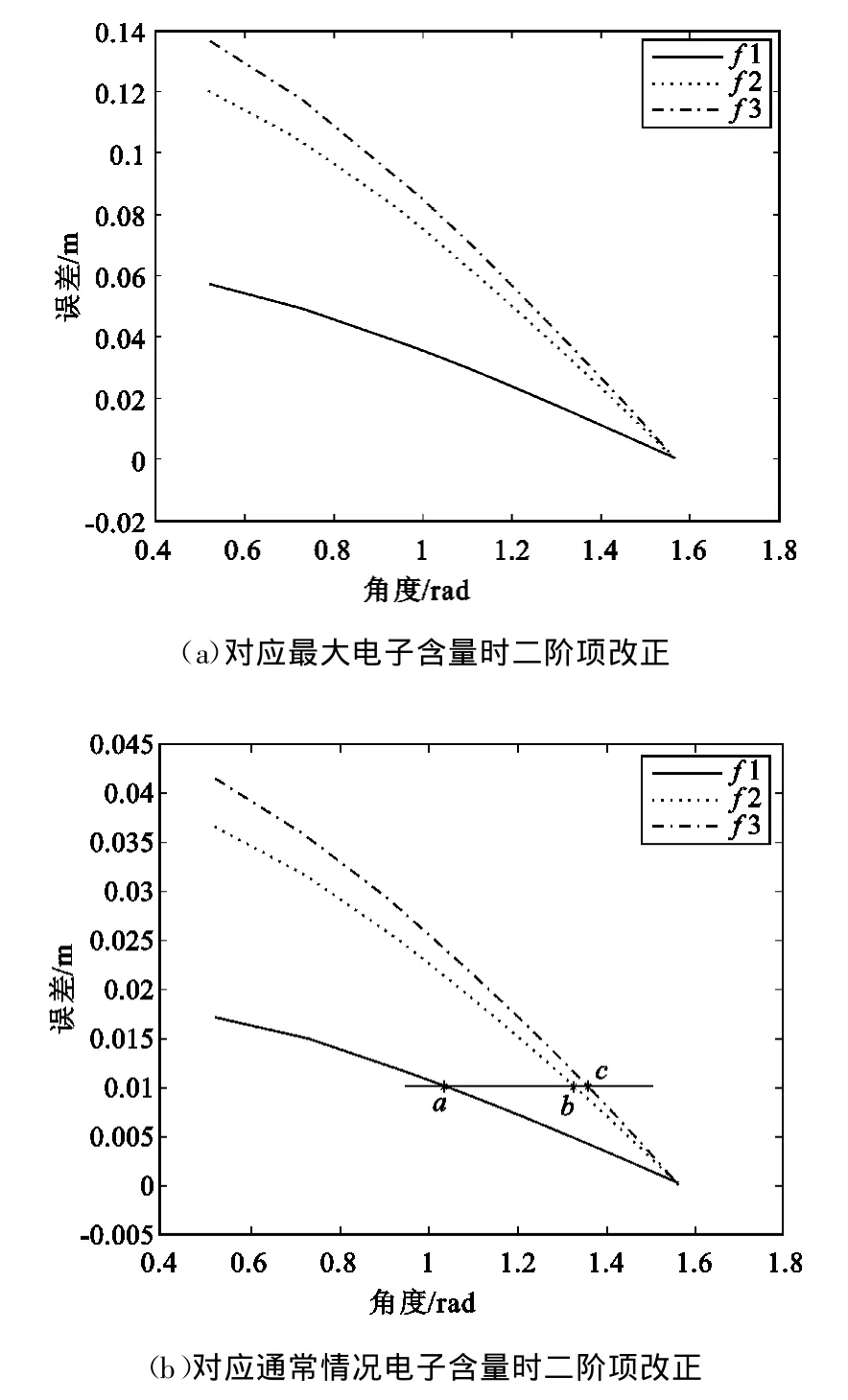
图1 延迟误差与角度的关系Fig.1 Relationship between delay error and the angle
5 总 结
本文在分析并利用电离层相折射率的基础上,系统地利用3个频率对电离层延迟误差的二阶项分别从伪距和载波相位两方面进行了修正。在分析 θ角的过程中,对二阶项的部分变量进行了定量分析,因此成功对二阶项的误差值与角度的变化进行了数据拟合,得到不同频率二阶项误差值与角度变化的函数图形。由函数图形可以清晰地看出不同的误差值对应的夹角,通过曲线方程计算出了3个频率在一般情况下二阶项修正值达到毫米级时的临界角度。二阶项修正精度与电磁波传播方向和地磁场方向的夹角θ密切相关,指出只有在一定的夹角范围内,才能达到理想的精度。研究的实用价值体现在:在相关领域的GPS精密定位中,基于本文给出的对θ角定量数据处理的方法,以及经实测获得的 θ角,可直接进行GPS电离层延迟误差的修正。
[1] 谢钢.GPS原理与接收机设计[M].北京:电子工业出版社,2009.XIE Gang.Principles of GPS and Receiver Design[M].Beijing:Publishing House of Electronics Industry,2009.(inChinese)
[2] 刘基余.GPS卫星导航定位原理与方法[M].北京:科学出版社,2003.LIU Ji-yu.Principles and Methods of GPS Satellite Navigation[M].Beijing:Science Press,2003.(in Chinese)
[3] 刘琪,张学军.三频GPS改正电离层折射误差高阶项的方法[J].航空电子技术,2006,37(3):13-15.LIU Qi,ZHANG Xue-jun.GPS Triple-Frequency Methods of High-Order Ionospheric Refraction Correction[J].Avionics Technology,2006,37(3):13-15.(in Chinese)
[4] Zemin Wang,Yue Wu.Triple-Frequency Method for High-Order Ionospheric Refractive Error Modelling inGPS Modernization[J].Journal of Global Positioning Systems,2005,4(1-2):291-295.
[5] 李征航,陈锴,刘万科,等.顾及f3项的电离层延迟模型[J].武汉大学学报(信息科学版),2007,32(2):139-143.LI Zheng-hang,CHEN Kai,LIU Wan-ke,et al.Ionospheric Delay Model Containing f3 Term[J].Geomatics and Information Science of Wuhan University,2007,32(2):139-143.(in Chinese)
[6] Brunner F K,Gu Min.An improved model for the dual frequency ionospheric correction of GPS observations[J].Manuscripta Geodetics,1991(16):205-214.

