分布式压缩的图像关联重建方法

刘 杰,陈怀新

(中国西南电子技术研究所,成都 610036)

1 引 言

图像能够提供给人们很多直观的信息,比较符合人类的认识规律,因而在多媒体通信、计算机系统、医学、物理等众多领域得到了越来越高的重视。但图像一般具有庞大的数据量,对于通信传输网络来说,受限的带宽成为了阻碍其传输速度进一步加快的瓶颈;为了解决该问题,人们提出了许多有效的压缩处理方法,如 JPEG[1]、JPEG2000[2]、压缩感知[3]等。通过压缩减少了通信网络传输的数据量,但这些方法在对分布式压缩的图像数据进行重建的时候均采用子图像的分别还原再拼接成完整图像的技术,在解码端具有计算量和存储量大的缺点,不能明显地提高通信传输网络的传输效率。

本文在基于小波变换的JPEG2000压缩体制基础上,提出了基于系数整合法的分布式图像压缩处理方法,本方法通过对原图像进行分块小波变换获得子图像小波系数向量,通信传输网络只分别传输图像压缩的子图像小波系数向量,从而大大降低了压缩编码系统的数据传输量;再对图像压缩解码的子图像小波系数进行关联处理,形成原图像的整体小波变换系数向量,并通过小波反变换进行原图像的重构。相较于传统的处理方法,本方法无需直接进行子图像还原及其图像的拼接处理,因而能有效缓解解码端较大数据量存储要求和复杂的图像配准与拼接计算。最后,本文采用MATLAB仿真,对结果进行了详细的数值分析。

2 基于小波变换的图像压缩方法

为了突破通信传输网络带宽受限的瓶颈,发展了许许多多的图像数据压缩方法,现在运用的最多也是最成熟的技术就是JPEG2000图像压缩标准。

2.1 离散小波变换

离散小波变换[4]在图像压缩处理中得到应用,采用图像小波变换系数的编码压缩体制已取代离散余弦变化成为图像压缩的新标准。

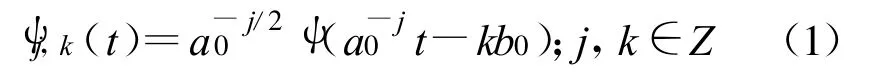
以此为基函数,所构造的小波变换就是离散小波变换:

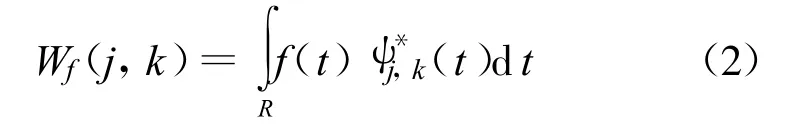
其逆变换如下:

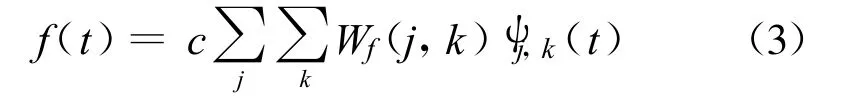
2.2 JPEG2000图像压缩方法

于2000年问世的静止图像压缩标准JPEG2000在编码端采用n×n的分块图像离散小波变换获得不同分辨率频段系数,然后进行量化编码得到了图像压缩数据;在解码端进行符号解码后,对分块压缩数据进行小波反变换得到 n×n的子图像,再将这些子图像进行简单拼接得到完整的大图像[5],其简要框图如图1所示。

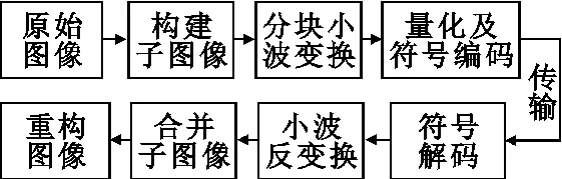
图1 JPEG2000压缩框图Fig.1 The compressed diagram of JPEG2000

图像经过小波变换后被分割成水平、垂直、对角线和低频4个频带,低频部分还可以继续分解。水平、垂直和对角线部分表征了原图像在3个方向的边缘信息,具有明显的方向特性,低频部分代表着图像整体的亮度信息。根据人类视觉的生理和心理特点,对4个部分分别作不同策略的量化和编码处理,就可以实现图像的压缩[6]。

3 基于系数关联整合的分布式图像压缩法

不同于传统的方法,基于系数整合(CC)法的分布式图像压缩过程在编码端先将图像分块,再进行子图像小波变换及子图像小波系数的量化编码,解码端进行小波系数的符号解码与关联整合,最后通过小波反变换实现原始图像重构,其简要框图如图2所示。

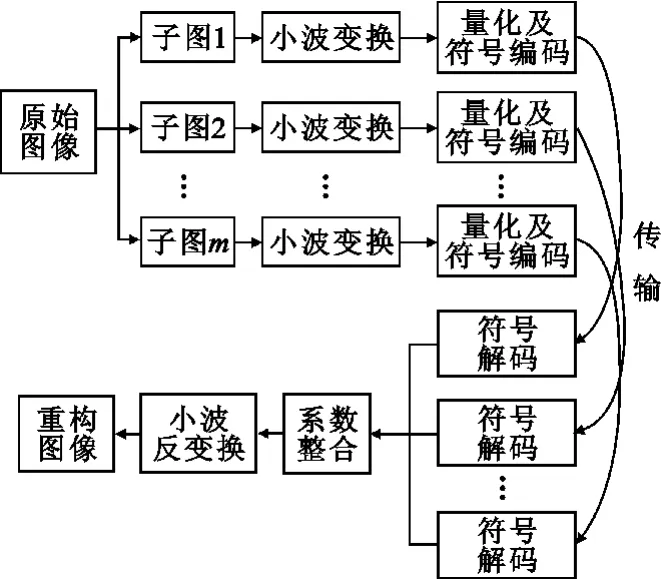
图2 基于CC法的分布式图像压缩框图Fig.2 The compressed diagram of distributed image based on coefficient conformity

在通信网络的解码端,如果进行子图像的分别还原再拼接成原图像反馈给计算机就需要进行复杂的计算和占用大量的存储空间,在这种情况下,对系数进行整合就显示出了其优点,不需要存储大量的图像数据,只需将能重点反映图像信息的系数进行整合,最后将这些系数反馈给计算机终端,将较大的计算量交给功能强大的计算机去完成,这也达到了资源合理利用的目的。

本文提出的分布式图像压缩系数关联整合处理如下。

首先,将一副N×N的原始图像f(u,v)进行分块,子图像块大小为n×n,共分成m个子图像,这m个子图的灰度值可表示为

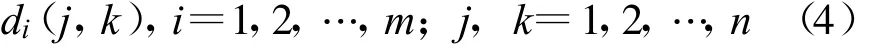
其次,每个子图像进行离散小波变换(CC法基于haar小波)得到4个频带信息。

低频方向为

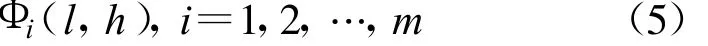
水平方向为

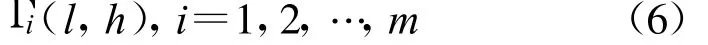
垂直方向为

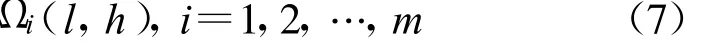
对角线方向为

式中 ,l、h=1,2,…,n/4。

量化和编码以及反量化编码技术已经相当成熟,可以用霍夫曼编解码[7]、循环编解码[8]等技术进行处理,由于这不是本文研究的内容,在这里就不进行详细论述了。

考虑到传输过程中存在着噪声影响,所以将接收到的各频带信息分别表示为

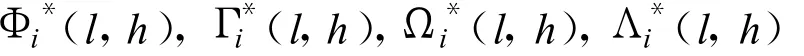
本文定义 Θq(l,h)为矩阵位置信息,定义Γi(l,h) Θq(l,h)为将 Γi(l,h)的值赋给合成的系数矩阵的第q块的对应位置。

再次,进行分块压缩编码系数的关联与组合处理。下面分无重叠和有重叠分块的情况来分别讨论系数关联整合。

(1)无重叠分块的情况

低频方向的系数关联整合如下:

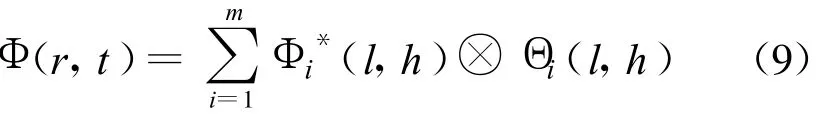
水平方向的系数关联整合如下:

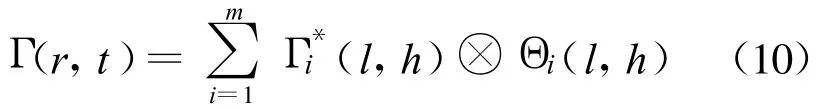
垂直方向的系数关联整合如下:

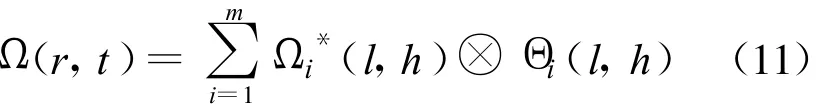
对角线方向的系数关联整合如下:

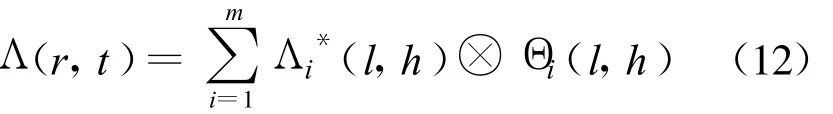
式中 ,r、t=1,2,…,N/4。

(2)有重叠分块的情况

假设在分块的时候相邻块均重叠,由于m个子图像运用不同的处理器进行处理,在进行系数关联整合的时候重叠部分将进行加权整合,因为在实际应用中各处理器的测量精度可能不同,则对其赋予不同的权值,将精度高的处理器赋予高的权值,反之,对精度较低的处理器则赋予较低的权值。令aj表示第j个处理器的权值,并且满足0≤aj≤1,那么可得各个方向的关联整合系数如下。

低频方向的关联整合系数:

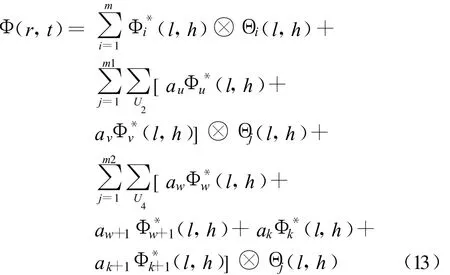
式中,第一项为无重叠部分的整合,第二、三项分别为两块重叠、四块重叠部分的加权整合,且满足 au+av=1和aw+aw+1+ak+ak+1=1。同理可得其它3个方向的关联整合系数。

在整合分块的小波系数基础上,通过小波反变换进行原图像的重构。

4 仿真及结果分析

本文以256×256像素的Lena图像作为仿真的对象,图像大小为65 kbyte,分别将图像分成无重叠和有重叠的4块,无重叠分块的每块为128×128像素、16 kbyte,有重叠分块的每块为136×136像素、18 kbyte。假设数据在传输的过程中受到服从标准正态分布的高斯白噪声的影响,并根据本文第2.2节的方法和第3节提出的新方法,在MATLAB 7.8.0环境下进行图像压缩的数值仿真分析。

(1)仿真实验1:无重叠分块压缩的仿真

对图3所示无重叠分块压缩的还原效果如图4所示。

图3 无重叠的分块Fig.3 The division without overlap

图4 无重叠分块压缩的还原效果Fig.4 The reconstructed effect of the division without overlap

为了直观地反映数据处理时效性,本文比较JPEG2000技术和基于CC法的分布式图像压缩处理方法(本文方法)的计算量,并采用图像数据解压重建时间(TOR)来衡量计算量大小。图像的还原质量通常可利用峰值信噪比、均方信噪比、均方根误差以及平均误差和(Mean Sum of Error,MSE)等来表示,本文采用原始图像和解压重建图像对应像素之间灰度值的MSE来评估图像还原质量,其计算公式如下:

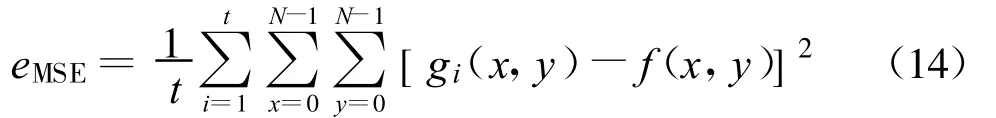
式中,t为仿真次数,gi(x,y)为第 i次仿真还原图像的灰度值。

为了得到准确、可靠的分析结果,需要通过大量的重复实验来获得实验数据,本文利用5000次的仿真来得到所需的仿真验证结果。

基于CC法的无重叠分块的分布式图像压缩和JPEG2000的图像还原效果对比如表1所示。

表1 无重叠分块压缩的还原效果Table 1 The reconstructed effect of the division without overlap

(2)仿真实验2:有重叠分块压缩的仿真

基于CC法的有重叠分块(图5)的分布式图像压缩和JPEG2000的图像还原效果对比如表2和图6所示。

表2 有重叠分块压缩的还原效果Table 2 The reconstructed effect of the division with overlap

图5 有重叠的分块Fig.5 The division with overlap

图6 有重叠分块压缩的还原效果Fig.6 The reconstructed effect of the division with overlap

从图4和图6可以看出,基于CC法的有重叠和无重叠的分布式图像压缩还原的图像效果很好,不论是JPEG2000还是基于CC法的分布式图像压缩处理方法,还原出来的图像和原始图像之间看不出任何明显的差异,这说明了基于CC法的分布式图像压缩处理通过系数关联整合的方法是有效和可行的。

对处理时效性利用解压重建时间进行仿真对比分析,结果表明基于CC法的有重叠和无重叠的分布式图像压缩处理的解压重建耗时分别为JPEG2000的1/8.8和1/17.6,若解码端的计算处理能力远低于功能强大的计算机,处理时间将按比例的扩大,基于CC法的分布式图像压缩处理方法的优势在实际运用中将会体现得更加明显。

从平均误差和的结果可以看出,通过大量的重复仿真,基于CC法的无重叠分块的分布式压缩处理方法的误差与 JPEG2000相当,其值略小于JPEG2000;基于CC法的有重叠分块的分布式压缩方法的误差值比JPEG2000少了22.7%,这说明,两种基于CC法的分布式压缩方法都比JPEG2000的抗高斯白噪声影响能力强,基于CC法的有重叠分块的分布式压缩方法效果更加明显。有重叠的分块方法通过牺牲少量的存储和传输代价换来了较高的抗噪声性能,对重叠部分的系数加权处理有效地减少了噪声对传输信号的影响。

实际应用中,在不明显提高存储量和计算压力的前提下,可以通过重叠分块的方法来达到较好的图像还原效果。

5 结 论

本文在JPEG2000的基础上,提出了基于CC法的分布式图像压缩处理方法。本方法将较大数据量的图像数据分解为多个数据量较小的子图像,再对子图像进行小波分解,可以大大减少单个编码系统的压缩编码数据;采用分块小波系数关联整合处理,避免了传统方法直接进行子图像还原及其图片配准拼接处理,有效缓解了解码端的存储和计算压力,并且具有很好的图像重建效果。通过仿真验证了本算法的有效性,其抗噪声性能也优于传统的JPEG2000图像压缩结果。这为大数据量图像信息在带限通信网络中高效传输提供了一种可行的方案,具有较高的实际应用价值。

[1] 罗倩玲.JPEG编码与矢量量化编码方法比较[J].电子测量技术,2005(4):35-37.LUO Qian-ling.The compare of coding between JPEG and vector quantization method[J].Electronic Measurement Technique,2005(4):35-37.(in Chinese)

[2] Varma K,Bell A.JPEG2000-choices and trade offs for encod-ers[J].Signal Processing Magazine,2004,21(6):70-75.

[3] David L Donoho.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.

[4] 张贤达.现代信号处理[M].北京:清华大学出版社,2002:384-386.ZHANG Xian-da.Advanced Signal Processing[M].Beijing:Tsinghua University Press,2002:384-386.(in Chinese)

[5] 李定川.JPEG2000图像压缩标准及其关键算法的应用[J].影像技术,2010(4):26-31.LI Ding-chuan.The imagecom pressed standard of JPEG2000 and appliance of its pivotal algorithm[J].Video Technique,2010(4):26-31.(in Chinese)

[6] Woods J W,Naveen J.A Filter Based Bit Allocation Scheme for Sub band Compression of HDTV[J].IEEE Transactions on Image Processing,1992,1(7):436-440.

[7] ISO/IEC 10918-1,ITU-T Rec.T.81(JPEG),Digital compression and coding of continuous-tone still images[S].

[8] Jovanovic V M,Budisin S C.On the Coding Gain of Linear Binary Block Codes[J].IEEE Transactions on Communications,1984,32(5):635-638.