城市轨道交通行人通道路阻函数拟合

张晓军 张 宁 陈 晖

(1.东南大学教育部ITS研究中心,210096,南京;2.嘉兴市铁路建设办公室,314000,嘉兴∥第一作者,硕士研究生)

城市轨道交通行人通道路阻函数拟合

张晓军1张 宁1陈 晖2

(1.东南大学教育部ITS研究中心,210096,南京;2.嘉兴市铁路建设办公室,314000,嘉兴∥第一作者,硕士研究生)

介绍了由BPR函数拓展而得到的轨道交通站厅内行人流条件下的路阻函数形式,并对其影响因素进行分析。在此基础上,对南京地铁新街口站自动扶梯和人行楼梯上的行人流进行实地调查,用实测数据拟合确定了南京城市轨道交通行人通道的路阻函数模型。研究结果表明,经由实测数据标定得到的路阻函数模型拟合效果较好,可以为轨道交通车站内设施布设等运营决策提供理论参考。

城市轨道交通;客运通道;行人交通流;路阻函数;关系拟合

First-author's addressITS Institute of Ministry of Education,Southeast University,210096,Nanjing,China

随着城市轨道交通客流量的急剧增长,一系列问题随之而来。如:轨道交通站厅客运通道内客流量超过自动扶梯、人行楼梯和售检票等设施的服务能力时,产生拥堵进而影响其服务水平,直接导致轨道交通系统运行效率下降,更甚者会发生交通事故。为此相关学者曾对城市轨道交通车站行人行程时间与流量的关系进行了广泛研究[1-4]。其中,香港学者根据对地铁行人流的调查不仅拟合出了站厅内纵向行人设施上的行人出行时间函数,还建立了行人路线选择模型,但地域的差异使得研究结果间存在着很大的不同;Ye Jianhong等[4]针对上海地铁站内行人设施中的单向通道、双向通道及人行楼梯上的行人流分别进行调查,得到了其行人流的流量-密度模型和速度-密度模型;并通过比较分析,得到了不同设施上行人流特性,在一定程度上完善了行人流理论。但其并没有对行人设施中自动扶梯上的行人流进行调查。而人行楼梯和自动扶梯上的行人流调查分析可用于行人路径选择模型,能更好地提高轨道交通服务水平。鉴于上述情况,本文将道路阻抗函数(以下简为“路阻函数”)概念拓展到轨道交通领域,分析了轨道交通站厅客运通道行人路阻函数的影响因素;同时以南京地铁新街口站为例,根据实测数据重点研究了国内轨道交通站厅客运通道中自动扶梯与人行楼梯上行人速度与流量的关系,并与以往研究成果进行对比分析。

1 行人路阻函数概念

路阻函数的概念在道路交通工程领域得到了广泛的应用,它是指路段行程时间(或车速)与交通负荷之间的函数关系。路阻函数在道路交通规划和交通控制工作中起着关键作用,国内外对其进行了大量的研究[5-9]。城市道路中路阻函数模型计算普遍采用经验回归模型,较为广泛使用的是美国公路局(U.S.Bureau of Public Roads,BPR)提出的BPR函数。该函数是美国公路局在对大量路段机动车流进行调查的基础上,通过回归分析得到的一个公式,具有通用性好的特点[10]。

行人流具有一般交通流的共性,BPR函数同样适用于轨道交通行人通道内行人流的研究,但函数中各参数的意义对应发生了改变。如式(1)。

式中:

t(v)——当行人流量为 v时,行人处于自动扶梯、人行楼梯上的行程时间,s;

t(0)——当行人流为自由流时,行人处于自动扶梯、人行楼梯上的行程时间,s;

v——行人流量,人次/(m·min);

C——行人通行能力,人次/(m ·min);

α,β——待定参数。

本文所研究的轨道交通行人通道内的行人路阻函数,既反映出行人处于自动扶梯及人行楼梯上的行程时间与其饱和度之间的函数关系,又反映了自动扶梯及人行楼梯上行人速度与行人流量之间的函数关系。

2 行人路阻函数的影响因素分析

从以往研究结果可以看出,不同地域得到的行人路阻函数有所区别,因此有必要对其影响因素进行分析。影响行人路阻函数模型的主要因素有自动扶梯与人行楼梯的设置方式、技术参数,以及行人流量和行人交通特征等。

2.1 自动扶梯与人行楼梯的设置方式

自动扶梯和人行楼梯是轨道交通车站内部楼层之间的重要交通设施,其设置是否合理是反映轨道交通车站服务质量的主要指标之一。自动扶梯与人行楼梯在设置方式上有一定的原则:根据各站客流不同分设上、下行自动扶梯;重要车站(装修标准为一级的车站)站台至站厅均设置上、下行自动扶梯;不同的提升高度,自动扶梯的设置也不同(主要设置参数见表1[11]);人行楼梯宽度＞3.6 m时应设置中间扶手。自动扶梯与人行楼梯的设置方式是影响站厅内行人路径选择的一个重要因素,设置方式不同,行人路阻函数模型也会不同。

2.2 自动扶梯与人行楼梯的技术参数

自动扶梯与人行楼梯的技术参数都是影响其设计通行能力C0的重要因素。例如,自动扶梯的运行速度、倾斜角度、梯级宽度、水平运行梯级数量,以及人行楼梯的宽度、倾斜角度、休息平台长度等,任何一项参数的变动都会影响C0的取值,进而影响到行人路阻函数模型中参数的标定。

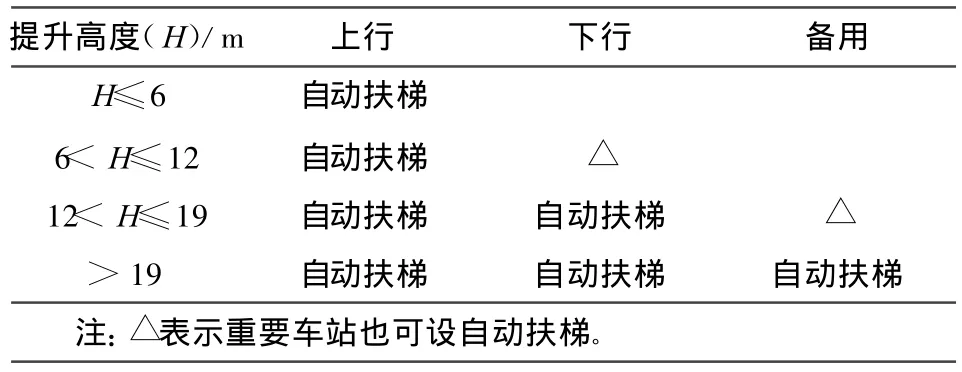
表1 自动扶梯设置参数

2.3 行人流量

在不同的行人流量下,行人的速度分布有很大差异。在低流量情况下,由于行人可根据自己的意愿自由控制行走速度,行人的速度波动很大,分布分散,规律性不强;随着行人流量的增加,由于行人密度增大,行人对速度的控制能力变弱,行人的速度分布越来越集中。因此,调查过程中的行人流量会在很大程度上影响到由速度拟合出的模型的效果。反之可以通过行人路阻函数模型的拟合,研究评价客运通道设置的合理性。

2.4 行人交通特征

行人交通流有着与机动车流完全不同的特性,如其速度较低、机动性和随机性更强、行人个体具有多样性和脆弱性等[12]。行人交通特性主要表现在行人的速度、对个人空间的要求和步行时的注意力等方面,它们与行人的年龄、性别、出行目的、教养及心境等有关,也与行人所处的区域、周围的环境、行人流量等有关。地域不同,行人的交通特性会有所区别。如中国人的步速、步幅、步频平均值会略小于国外人士。这是行人路阻函数通用性不高、移植性不强的主要原因。

3 行人路阻函数的调查

为得到适用于国内城市轨道交通站厅通道的行人路阻函数模型,笔者以南京地铁车站为例进行了实测调查。

3.1 行人路阻函数的调查方法

行人路阻函数的调查方法主要有录像法和人工调查法两种。录像法的最大优点是可以重现事件,但后期数据处理工作繁杂。人工调查法后期数据处理工作相对简单,但不能重现事件以实现对调查数据的修正。综合考虑本次调查的目的和可操作性,经权衡对比选用人工调查法。为弥补人工调查法的不足,尽可能减少误差,在调查前对调查人员进行了严格的培训。

3.2 行人路阻函数的调查地点

行人路阻函数的调查地点为南京地铁新街口站。在调查地点的选择上主要考虑两点:车站的客流量是否足够大;车站内部自动扶梯或人行楼梯的设置方式是否为国内主要设置方式(国内主要设置方式为上行自动扶梯和人行楼梯,其中人行楼梯宽度为3.6 m)。从南京地铁公司提供的资料看,南京地铁新街口站客流量在高峰时间段接近饱和,列车运行间隔短;自动扶梯或人行楼梯的设置方式为上行自动扶梯和人行楼梯,人行楼梯宽度为3.6 m,满足上述两点内容。

3.3 行人路阻函数的调查内容

人行楼梯的功能没有严格意义上的划分,其主要是为下行人流服务;但当上行人流较大时,行人往往会舍弃自动扶梯而使用人行楼梯,因此人行楼梯在一段时间内会同时被下行人流和上行人流占用,行人流特性较为复杂。此外,在实测调查中发现,由于自动扶梯进口处较窄,进口处的行人流存在一定延误,其行人流特性与自动扶梯上的行人流有着显著区别。为此,本次调查针对自动扶梯的上行人流及进口处一段距离内的行人流、人行楼梯的上下行人流分别展开。调查在新街口站高峰时间进行,历时4 h,调查记录时间间隔为30 s。调查内容包括:

(1)行人流量;

(2)行人在自动扶梯、人行楼梯上的时间;

(3)自动扶梯与人行楼梯的尺寸,包括自动扶梯的提升高度、有效净宽,人行楼梯的提升高度等,具体设施尺寸参数见表2;

(4)进口处行人流调查中距离的选用及其行程时间,所用距离定为9.8 m。

表2 设施尺寸参数

4 行人路阻函数调查分析

将调查得到的实测数据导入Access软件,利用时间关系建立数据库。具体分析过程见图1。

对实测数据进行分析,主要为获得用于分析的自动扶梯与人行楼梯的通行能力C、不同时间段的行人流量v及与此相对应的步行时间t(v)、在自由流条件下行人的步行时间t(0)等参数。对于BPR函数中t(0)的取值计算,需要设定行人流为自由流的条件。根据以往对行人流的研究,将行人流为自由流的条件设定为v≤30人次/(m·min)、行人占有空间＞2.3 m2/人[13]。数据分析得到的各参数见表3。表中同时列出了调查中得到的行人流量最大值Cmax、我国地铁设计规范中的设计通行能力C0、香港地铁研究中所用的通行能力CHK及伦敦地铁研究中所用的通行能力CL[1,3]。从表3中可以看出,各通行能力有所区别。结合Cmax、C0和CHK,并考虑调查过程中人行设施上的行人流未达到饱和,确定了C值。与CL相比较,C和CHK偏大,这符合亚洲城市行人对空间要求相对较小的特性。

图1 数据分析流程图

由行人在自动扶梯、行人楼梯上的时间与其饱和度的散点图(图5)可以看出,其分布呈现一定的规律性,但由于样本选择的随机性,一个流量值往往对应不同的行程时间。为减小由于行人的随机性而产生的误差,在拟合前需先计算出t(v)的平均值。在数据分析后,为方便进行拟合,将式(1)化简为含B和n未知量的幂方程:

由于式(2)中t(v)-t(0)可能会导致负值,而本文主要用于研究行人流过大的现象,因此在模型拟合过程中,舍弃t(v)小于t(0)的样本。为提高模型的精确度,在拟合过程中首先进行分段拟合,然后适宜选取特定的流量值,由分段拟合模型确定特定流量值的行人行程时间,最后对这些特定的散点进行拟合得到路阻函数模型。自动扶梯和人行楼梯上行人流特性的散点图和路阻函数拟合图见图2～5。

由图中相关度R2的值可以看出,标定得到的路阻函数模型精确度较高。模型中的参数B和n分别决定了曲线的斜率和凹凸性。当 n＞1时,B值和n值越大(或当n＜1时,B值越大和n值越

小),拟合曲线的斜率越大,凹凸越明显,行人的速度随流量变化越快。将拟合到的模型参数及以往研究成果列于表4中[3,14],以利于比较分析。对自动扶梯和人行楼梯,南京地铁和新加坡地铁对B的取值较为接近,比香港大出许多,表明前者行人的速度对流量的变化较后者敏感。对自动扶梯的上行人流n的取值,由于行人上行的速度主要取决于自动扶梯的运行速度,因此3个城市的取值都接近为1。对人行楼梯的行人流n的取值,南京地铁和香港地铁较为接近,而新加坡地铁只对下行人流进行了研究,其n值小于1;与B值联系起来可以看出,相对香港地铁,南京地铁和新加坡地铁的行人灵活性更大。

表3 行人路阻函数调查参数值

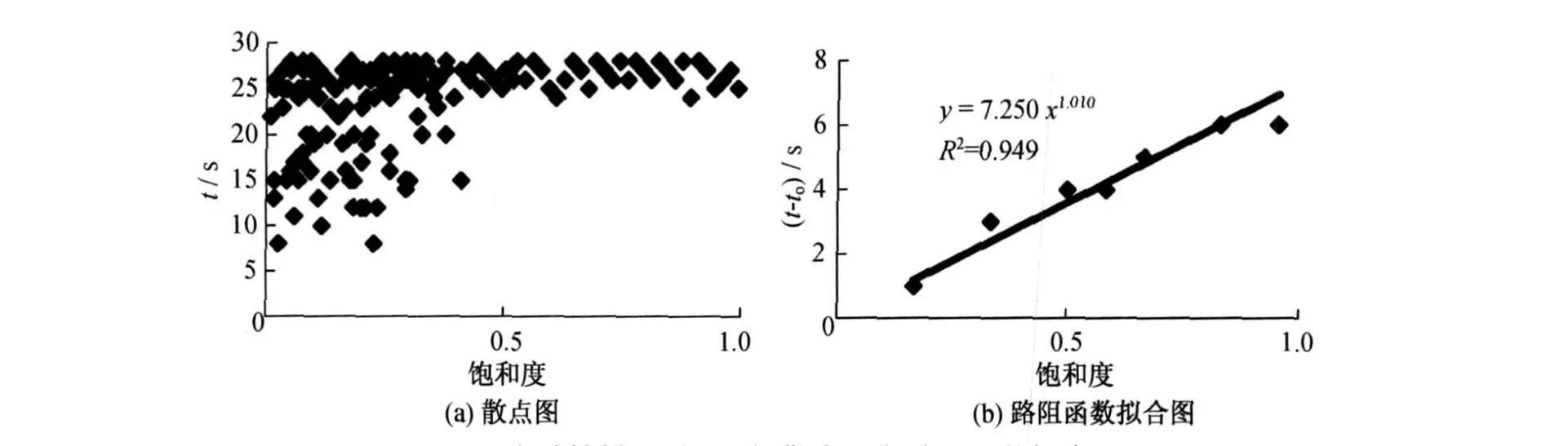
图2 自动扶梯(上行人流)散点图和路阻函数拟合图

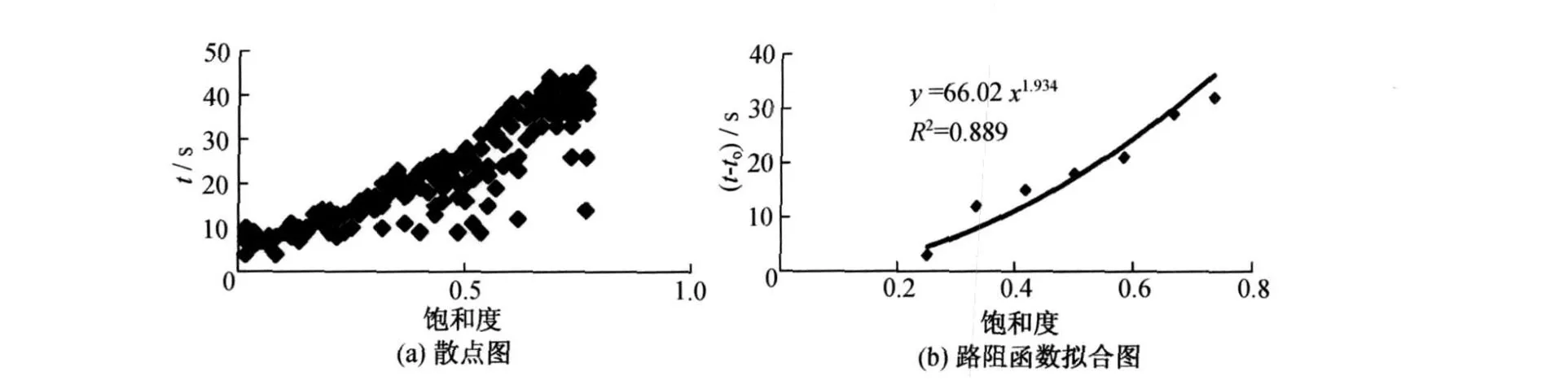
图3 自动扶梯(进口处人流)散点图和路阻函数拟合图

图4 人行楼梯(下行人流)散点图和路阻函数拟合图

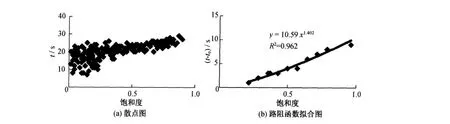
图5 人行楼梯(上行人流)散点图和路阻函数拟合图

表4 行人路阻函数参数拟合结果汇总

5 结语

自动扶梯及人行楼梯上行人路阻函数模型的确定对提升轨道交通系统的服务水平具有重要意义。合理的行人路阻函数可以正确指导车站内部设施的规划和设计,有效预防站厅内客流拥堵的产生。同时,其行人路阻函数可用于建立行人路径选择模型,解决行人设施利用不均衡的问题。本文通过对南京地铁新街口车站的具体调查和对实测数据的分析,拟合出的行人路阻函数模型效果较好,可为国内轨道交通车站内部行人设施布局等提供理论依据。

[1]Daly P N,McGrath F,Annesley T J.Pedestrian speed/flow relationships fo r undergrond stations[J].T ransportation Engineering and Control,1991,32(2):75.

[2]Harris N G.Modelling walk link congestion and the prioritisation of congestion relief[J].T ransportation Engineering and Control,1991,32(2):78.

[3]Cheung C Y,William W H K.Pedestrian routechoices between escalator and stairway in M TR stations[J].Journal of Transportation Engineering,1998,124(3):277.

[4]Ye Jianhong,Chen Xiaohong,Yang Chao,et al.Walking behavior and pedestrian flow characteristics for different types of walking facilities[J].Transportation Research Record,2008(2048):43.

[5]王炜,张桂红.城市道路路阻函数研究[J].重庆交通学院学报,1992,11(3):84.

[6]靳文舟,张杰,张旭莉.路阻函数的最大似然标定法[J].公路交通科技,1996,13(4):24.

[7]孟祥海,李士莲.大城市快速路及主干路路阻函数的研究[J].交通运输系统工程与信息,2005,5(4):31.

[8]王树盛,黄卫,陆振波.路阻函数关系式推导及其拟合分析研究[J].公路交通科技,2006,23(4):107.

[9]Xu Meng,Shi Zhongke.Outflow models based on velocity/density formulation used in dynamic traffic assignment[C]∥Proceeding s of 2005 International Conference on Machine Learning and Cybernetics.Guangzhou,2005:3568-3573.

[10]王素欣,王雷震,高利,等.BPR路阻函数的改进研究[J].武汉理工大学学报,2009,33(3):446.

[11]GB 50157—2003 地铁设计规范[S].

[12]陈然,董力耘.中国大都市行人交通特征的实测和初步分析[J].上海大学学报:自然科学版,2005,11(1):94.

[13]Fruin J J.Pedestrian Planning and Design[M].2nd ed.Alabama:Elevator World Inc,1987.

[14]Zhou Xiang,War K F,Chor C H.Pedestrian speed-flow model on escalators and staircases in Singapo re M RT stations[EB/OL].[2009-12-27].http:∥staff.science.nus.edu.sg/～scilooe/srp2003/sci_paper/civil/research%20paper/zhou_xiang.pdf.

Impedance Function's Fitting of Passenger Corridor in Urban Rail Transit

Zhang Xiaojun,Zhang Ning,Chen Hui

In order to improve the efficiency of urban rail transit passenger organization,evaluate the reasonable degree of facility layout at the stations,and further enhance the overall service level of rail transit system,this paper introduces the impedance function of pedestrian flow at urban rail transit stations,which is derived from the BPR function of the U.S.Federal Highway Administration(FHWA),analyzes the impact factors and defines the impedance function model of passenger corridor at urban rail transit stations,by using the measured data of pedestrian flow on escalators and stairs at Nanjing metro station.The results show that the fitting of the impedance function model is acceptable and can provide a theoretical reference of operational decision-making for the station's layout design.

urban rail transit;passenger corridor;pedestrian flow;impedance function;relationship fitting

U 231+.4

2009-11-19)