索网结构初始平衡状态的优化设计*

杜敬利 保宏 崔传贞

(西安电子科技大学电子装备结构设计教育部重点实验室，陕西西安710071)

采用优化策略进行求解，对于整个索网系统，为了使各控制节点尽量平衡在预定的位置上，可以得到如下的优化模型:

我国科学家提出的利用Karst盆地构建500 m口径大射电望远镜的计划正在进行中，利用盆地地形铺设主动反射面是该计划中极具创造性的部分.原方案中的主动反射面为机械分块式结构，造价很高.在已有的可行性研究基础上，文献［1］中提出了索网主动反射面方案，采用单层索网结构作为反射面板的支撑系统.设计要求索网反射面的初始状态平衡在半径R=300 m的观测球面上;系统观测时，通过改变调整索的长度(或拉力)，使反射面的照明部分能够实时地调整成瞬时抛物面，从而可用传统的点馈源照明技术实现宽带观测.与分块反射面方案相比［2］，索网主动反射面中控制节点的数目将大幅减少，从而极大地降低了工程造价.

文献［1］中每个控制节点都采用3根调整索进行调整，故可在一定范围内将控制节点定位到空间的任意位置.但这种设计方案需要精确地协调3根调整索的长度，微小的索长误差都会导致调整索的牵引力发生显著变化.此外，如果牵引力未进行适当规划还会导致索网各处的应力分布差距很大，不但会降低系统刚度，而且增加了调整难度.因此，文中在每个节点处均采用单根调整索进行调整，在与调整索垂直的方向上节点运动不受控制，这样有利于使索网系统平衡在一个应力分布较为均匀的状态.

索网结构只有在具有一定应力的情况下才能够承受外部载荷，因此必须确定一个具有某种预应力的初始平衡状态，这个过程通常称为找形［3］或初始平衡构型分析［4］.在大型现代化的索网设计中，提供一种高效、精确的初始平衡状态的分析方法是至关重要的.索网结构初始平衡状态确定时的常用方法是力密度法［5］，但它仅适用于线性索单元;另一种方法是动态松弛法［6］，可完成非线性结构的平衡态分析，该方法的主要思想是将静力学问题转化为动力学问题，故求解速度较慢.文献［7］中通过对索网结构的平衡矩阵进行奇异值分解来完成结构的平衡状态分析，但也只能用于线性索杆单元.也有一些学者采用优化方法进行求解［8］，但由于缺乏必要的敏度信息，故求解速度慢，计算量大.

索网结构分析时，常用的有限元法通常使用大量的索杆单元模拟单根柔索，计算量很大，并且容易出现数值收敛问题.为此，文中将使用精确的弹性悬链线解析表达式来完成单根柔索的力学分析以克服有限元法的不足.同时将结合索网反射面的具体设计要求，通过优化策略解决索网结构初始平衡状态的确定问题，从而可以在给定索网形状的前提下求解索段的初始长度及应力.

1 索网主动反射面的初始状态

大射电望远镜中的主动反射面结构如图1所示，其中索网索段的交汇点称为控制节点，由调整索与地基相连，其长度(或拉力)决定了反射面的形状.初始平衡状态分析的目的就是寻找恰当的网面索段长度(对应特定的应力状态)和牵引索张力，使得整个网面可以在给定位置处于平衡.

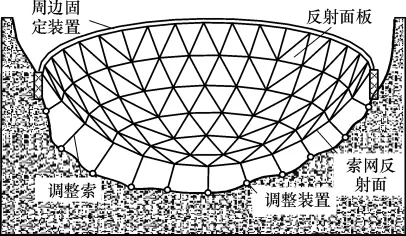
图1 索网主动反射面示意图Fig.1 Schematic plan of active cable-net reflector

索网主动反射面初始状态的形状是已知的，分析的目标是精确确定索段的初始长度和对应的应力状态以及相应的牵引力，使得索网的控制节点能够尽可能地平衡在指定位置.同时，索网的应力不能太大，以免索段发生破坏;而且，为避免结构刚度过低，牵引索也应具有一定的拉力.

由于反射面在工作状态下的形状精度要求很高，加之结构体系十分庞大，因此该结构初始状态的确定成为工程设计中的技术难点之一.

1.1 球反射面网面形状的确定

原型设计时采用初始六环三向索网，将球反射面划分为6个对称扇形曲面，网面的构成包括沿径向的主索、环向副索和连接内外层的次索，它们将球面网面划分成近似均匀的三角形网格，其俯视图如图2所示.这种形式的索网加工不太复杂，索网应力也比较均匀，整体性能较好.

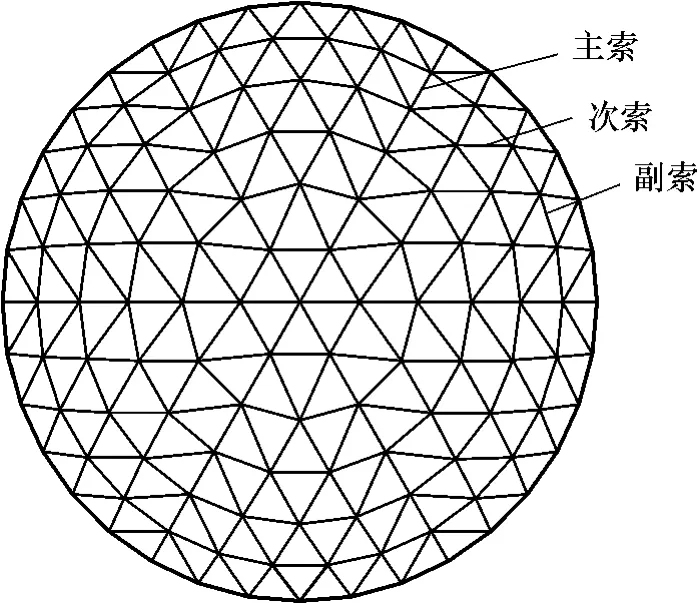
图2 索网主动反射面俯视图Fig.2 Top view of active cable-net reflector

1.2 索段初始长度及应力状态的确定

索段初始长度的精确确定是保证索网张拉成形后应力状态满足设计要求的关键，为此，分析时可以将索网中各索段的初始长度作为设计变量.考虑到初始长度与受力后的实际长度及应力状态是相互对应的，且将受力后的实际长度作为设计变量分析时更加方便，故文中将索段的实际长度作为设计变量.假设索网中共有n根索段和m个控制节点，记索段的实际长度为

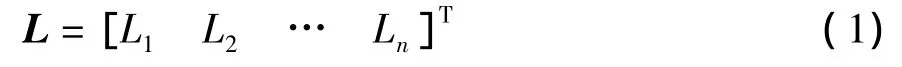
平衡时索网的应力状态为L的函数.

文献［9］中指出悬索的最大应力不应该超过许用应力(［σ］)的60%.因此认为平衡时索段c(c= 1，2，…，n)的应力σc应满足

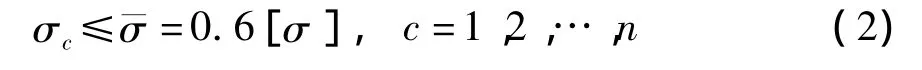
式中，¯σ为允许的应力上限值.

1.3 调整索张力的确定

每个控制节点上均采用单根调整索垂直网面向外牵引.为保证索网具有足够的刚度，牵引力应达到一定的强度.设牵引力Ti表示连接控制节点i的调整索的张力，则Ti应满足

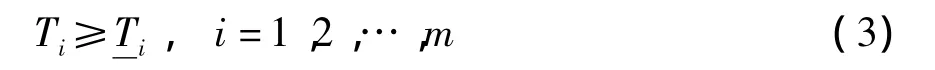
2 初始平衡状态的优化模型

初始平衡时控制节点在索网内力和牵引索张力共同作用下的合力应为零.选取索网中的某一控制节点i(i=1，2，…，m)，共有Ni根索段汇交于该节点，调整索将节点i与地基上的A点相连，由A指向i的单位向量记为si，如图3所示.

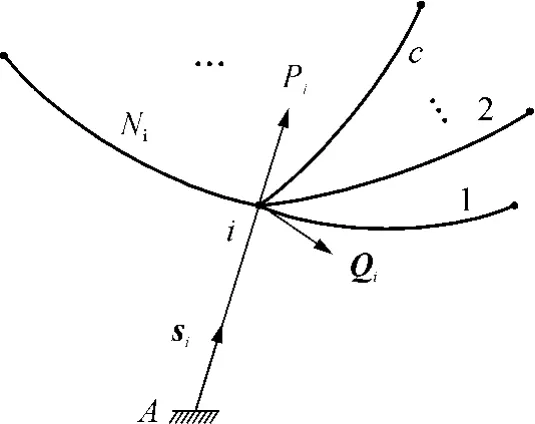
图3 索网中的某一控制节点iFig.3 A control node i of the cable-net structure

设交汇于i点的索段c(c=1，2，…，Ni)的两端节点分别为(其中一个为i)，由节点指向的向量在水平面内的投影单位化后记为a，同时c将沿坐标系Z轴方向的单位向量记为z.索段c对控制节点i的作用力可以表示为

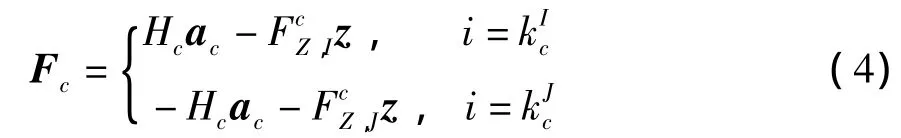
式中，Hc为索段c的水平张力，分别为索段c的I和J端所受的竖直向上的拉力.于是，索网对该节点i的合力沿si方向的投影Pi可以表示为

根据平衡关系，有Ti+Pi=0.而垂直于si方向的分量，即横向不平衡力Qi，可以表示为

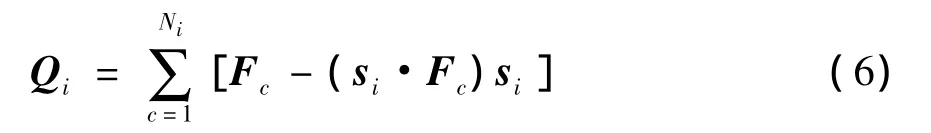
为避免开方运算，对Qi的模取平方有

考虑到柔索的最大张力一般发生在索端节点而不是中间某点，故仅将索段位置较高的端点对应的张力进行校验即可.为避免开方运算，将式(2)两端平方，得

式中，

Ac为悬索c的横截面积.

这样，为了使节点i保持平衡，应满足

采用优化策略进行求解，对于整个索网系统，为了使各控制节点尽量平衡在预定的位置上，可以得到如下的优化模型:

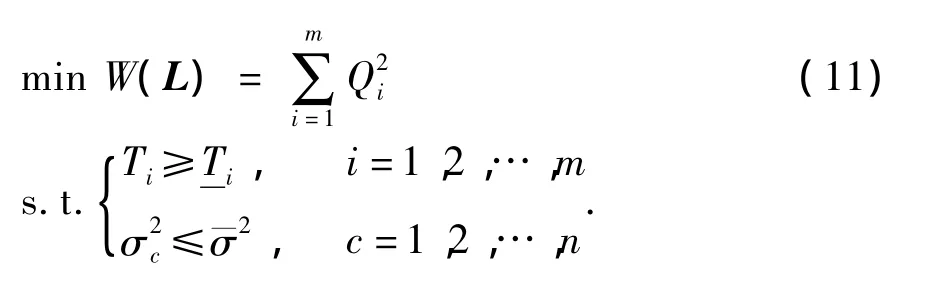
3 柔索静力学模型与敏度分析

3.1 柔索的静力学模型

索网结构分析时选择恰当的柔索力学模型是非常重要的.柔索受力后会伸长，并且呈现出高度的非线性特性，在长度上出现0.1%的误差将会导致柔索张力的偏差在50%以上［10］，为此，分析时使用弹性悬链线解析表达式以考虑索段的弹性变形.

假设索段是完全柔性的，无扭转刚度且只能承受拉应力，所用材料满足虎克定律.考虑如图4所示的柔索在自重作用下保持平衡，其弹性模量为E，横截面积为A，变形前单位长度的重量，即索的线密度为w0，初始长度为Lu，受力后的实际索长为L.定义重力的方向沿Z轴负向.

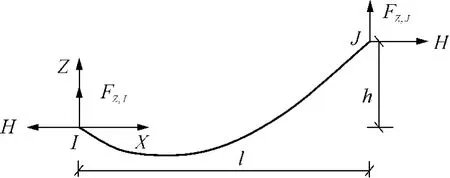
图4 柔索在自重下作用的平衡Fig.4 Equilibrium state of a cable with self-weight

整根柔索的水平张力保持不变，设为H，在两个端点I和J处分别受到竖直向上的拉力FZ，I和FZ，J.设端点I和J之间的水平跨距为l，竖直方向的高度差为h，此时柔索各物理量之间满足如下关系［11-12］:

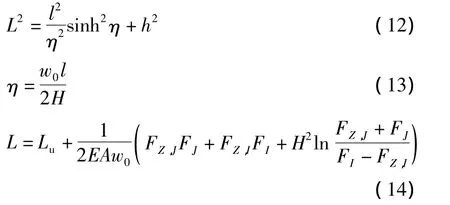
式中，

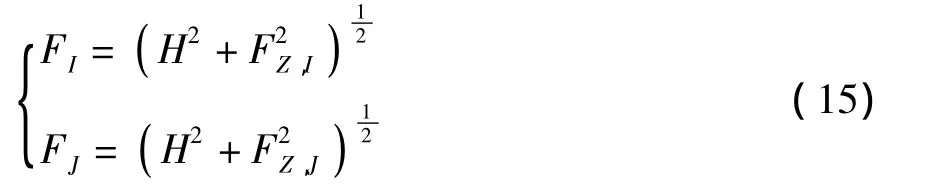
当柔索两端固定时，h、l均为已知量，可以得到实际索长L与η之间的非线性函数:

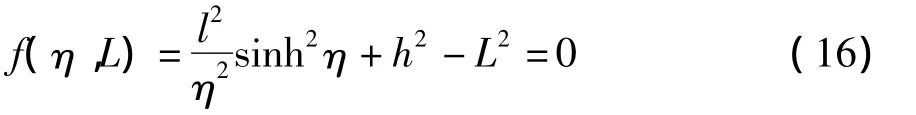
将式(16)对η求导得

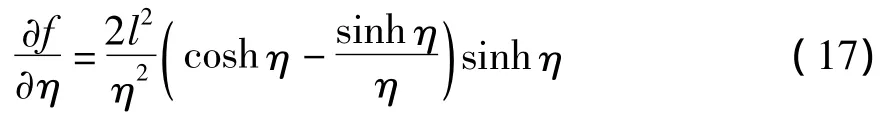
这样，应用单变量的 Newton-Raphson方法求解式(16)就可以得到与给定索长L对应的η，进而可由式(13)求得柔索的水平张力H.索段端点I和J处竖直方向的作用力FZ，I和FZ，J可表示为

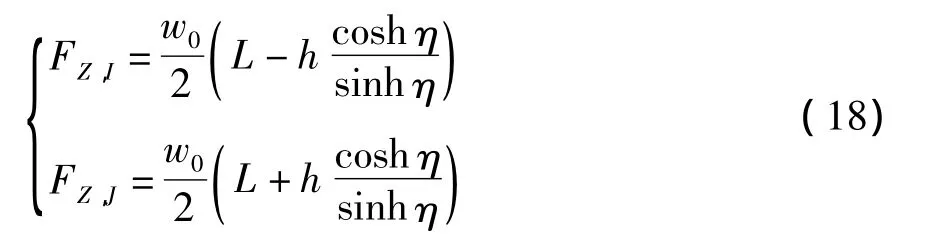
3.2 敏度信息的推导

由式(16)可得η关于L的导数为

对式(18)求导可得

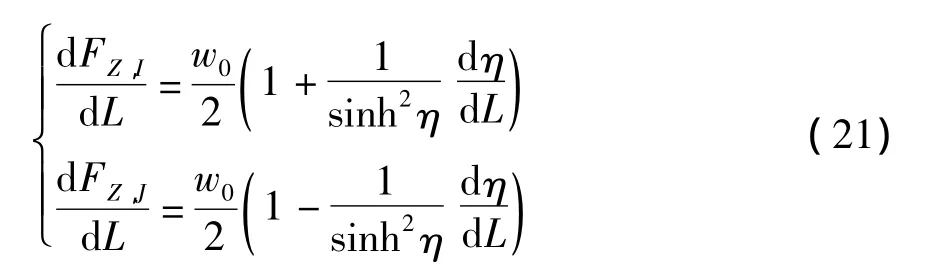
将式(4)对索段c的实际索长Lc求导可得

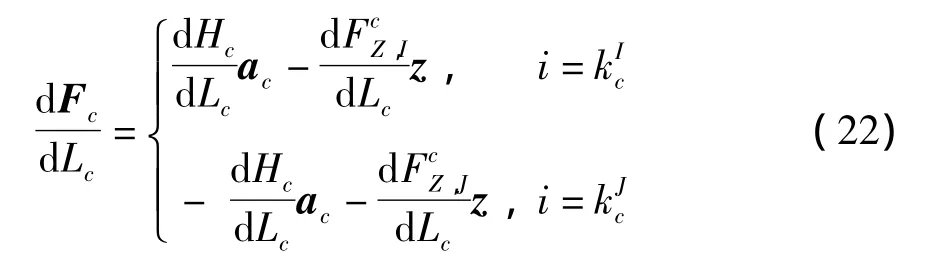
将式(7)对Lc求导可得

将式(6)对Lc求导可得

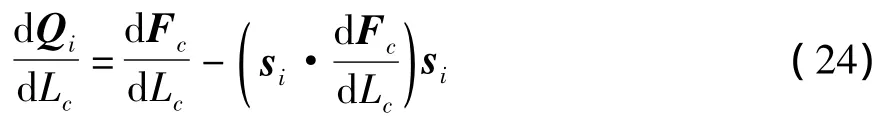
将式(8)对索长Lc求导，得

模型中各量及其梯度信息均已得到，采用序列二次规划(SQP)法［13］优化即可获得索段的实际长度L及其对应的索端张力，代入式(14)便可获得各索段的初始长度.

4 数值算例分析

该算例以50m模型中的相应参数为依据，要求索网节点不能太多以便于建造，同时还要具有一定数目的节点，以便能够直观地观察到瞬时抛物面从一个位置变化到另一位置.为此，将反射面按1∶10缩小，所用参数为:基本球面半径R=30m，口径D= 52m，网面环数Nm=6.索网中各索段的物理参数均相同:弹性模量E=2.058×1011Pa，横截面积A= 5.539×10－5m2，密度ρ=9.521021×103kg/m3.

在基本球面球心处建立直角坐标系O-XYZ，Z轴竖直向上，初始设计时假设各环主索对应的圆心角都相等，为Δθ=θ/(2Nm)，其中θ=120°.这样，对于第e环的索段，对应的节点构成边数为6e的正多边形，其半径为re=Rsin(eΔθ).

根据索网的对称性进行变量归并，其中的主索将索网分割成6个对称部分，每一部分中索长和调整索牵引力的归并如图5所示，共有30个独立的索长变量(图5中1－30)和12个独立的调整索牵引力变量(图5中(1)－(12)).

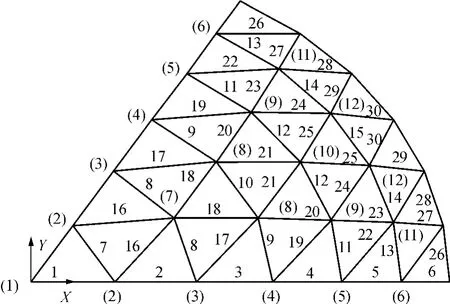
图5 索长及牵引力的变量归并Fig.5 Classification of variables for cable length and drag force

优化时取Ti=150 N，［σ］=150 MPa，初始值取实际索长为相应弦长的1.0001倍.目标函数的迭代过程如图6所示，经过75次迭代后达到291.87N2，此时控制节点上的最大横向不平衡力为3.8N.静力学分析平衡后索网节点的最大位移不超过0.62mm，完全满足精度要求.

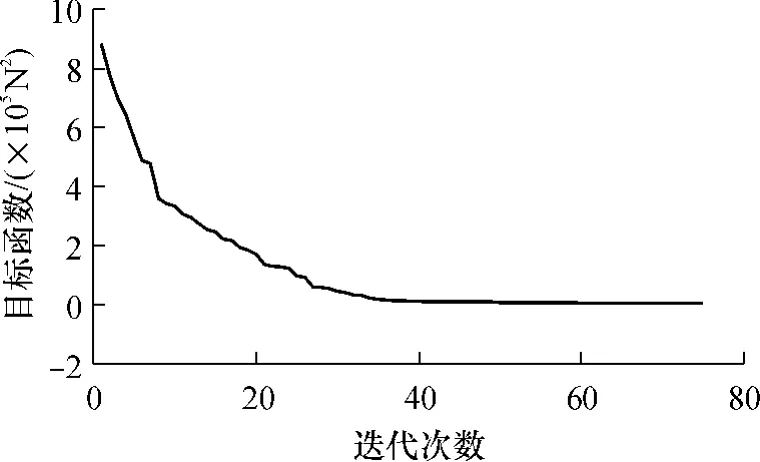
图6 目标函数的收敛过程Fig.6 Convergence history of objective function

优化后的索段初始长度在表1中列出，对应的索网张力分布如图7所示，此时各调整索牵引力在图8中给出，所有索段的应力均未达到规定的上限值.图7中索网索段的最大张力(1139.9 N)是最小张力(231.2N)的4.93倍，分别出现在索段1和索段6上，这是由于在网面的不同位置，三角形网格的形状相差较大，从而导致索力分布不均匀.为解决这一问题，可以将柔索张力的均匀性也作为目标函数同时进行优化.

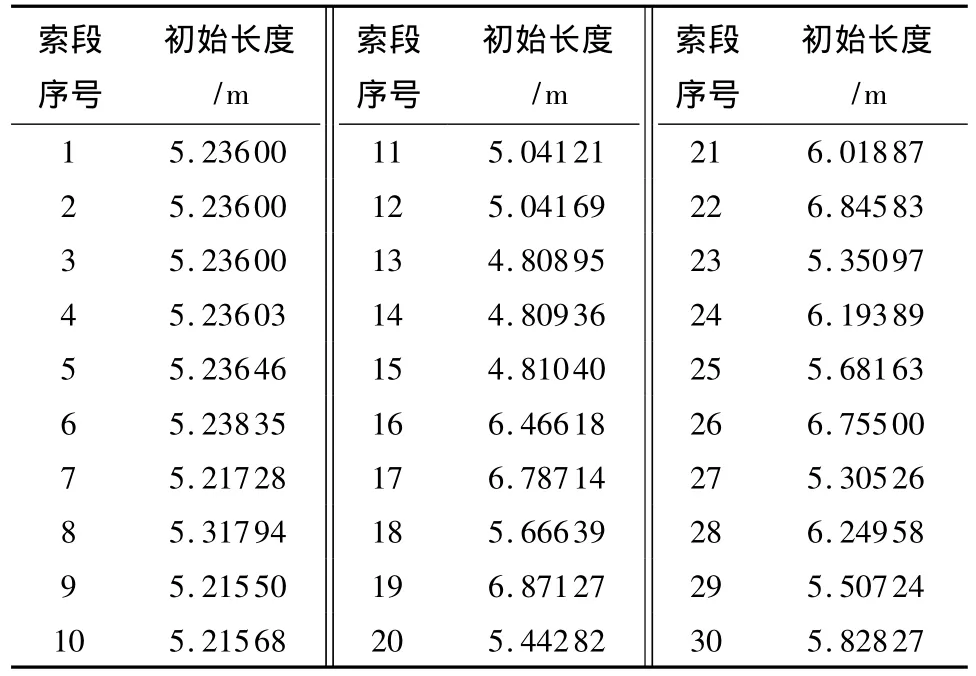
表1 索段的初始长度Table 1 Initial length of cable segment

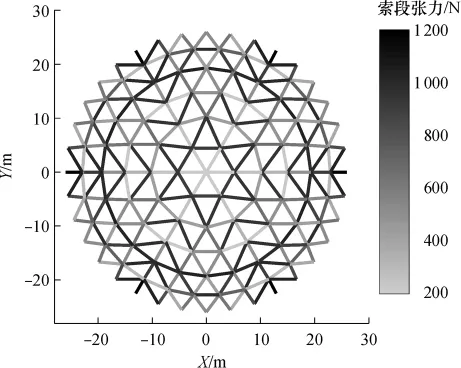
图7 索网的索段张力分布Fig.7 Tension distribution of cable segment in cable-net structure

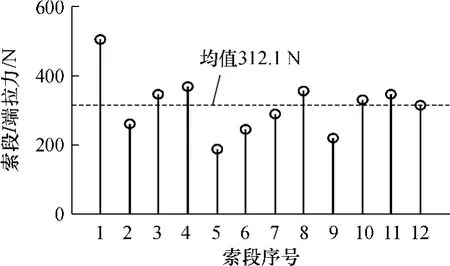
图8 调整索的牵引力Fig.8 Drag force of adjustable cables

要使调整索具有一定的拉力，索网应具有一定的应力.从图7中可以看出，索网均处于张紧状态，索段6和26的张力最小，因为在相同的张力作用下，索段26沿X方向的投影要比索段13大得多.

图8中调整索牵引力的差别不大，最大牵引力(502.90N)是最小牵引力(185.36N)的2.71倍，分别作用在节点1和节点5上.索引力的平均值为312.1N.

对比表1中的索段1和6，二者对应的弦长相等，索段1比索段6的初始长度仅减小了0.045%，但张力却增加了493.02%.这表明此时结构处于高度非线性状态，初始长度的精确确定是保证索网具有特定应力状态的关键.

5 结语

空间索网应力状态的确定是大型索网设计中的一个难点.文中建立了确定索网反射面初始平衡状态的优化模型，并推导出了优化所需的敏度信息.数值算例表明，采用该优化方法能够快速完成索网结构初始平衡状态的求解.

优化目标中的节点不平衡力是针对索段逐个叠加求解的，故可有效避免因结构整体刚度矩阵奇异而带来的数值收敛问题.这样，使用文中方法总可以得到最接近于给定形状的结构构型，同时还可进一步将索网应力状态的均匀性作为目标函数，从而得到更为理想的平衡状态.

［1］ Nan Rendong，Ren Gexue，Zhu Wenbai，et al.Adaptive cable-mesh reflector for the FAST［J］.ACTA Astronomica Sinna，2003，44(Suppl):13-18.

［2］ Luo Y，Deng C，Li G D，et al.Structural analysis of the FAST reflector supporting system and its model［J］.Astrophysics and Space Science，2001，278(1):231-236.

［3］ Nazmy A S，Abdel-Ghaffar A M.Three-dimensional nonlinear static analysis of cable-stayed bridges［J］.Computer and Structures，1990，34(2):257-412.

［4］ Sucha M，Jimenez-Octavio J，Carnicero A，et al.An approach based on the catenary equation to deal with static analysis of three dimensional cable structures［J］.Engineering Structures，2009，31(9):2162-2170.

［5］ Haber R B，Abel J F.Initial equilibrium solution methods for cable reinforced membranes(Part I):formulations［J］.Computer Methods in Applied Mechanics and Engineering，1982，30(3):263-284.

［6］ Han S E，Lee K S.A study of the stabilizing process of unstable structures by dynamic relaxation method［J］.Computers and Structures，2003，81(17):1677-1688.

［7］ 李刚，关富玲.环形桁架展开天线索网的预拉力优化技术及工程应用［J］.固体力学学报，2006，27(Suppl):174-179.Li Gang，Guan Fu-ling.Optimization of pretension in net of astromesh deployable reflector and engineering application［J］.ACTA Mechanica Solida Sinica，2006，27(Suppl):174-179.

［8］ 狄杰建，段宝岩，罗鹰，等.大型网状可展开天线预张力的优化［J］.华南理工大学学报:自然科学版，2004，32(6):23-26.Di Jie-jian，Duan Bao-yan，Luo Ying，et al.Preloading optimization of large net-shape deployable antennas［J］.Journal of South China University of Technology:Natural Science Edition，2004，32(6):23-26.

［9］ 罗永峰，于庆祥，陆燕，等.大射电望远镜反射面支承张拉结构非线性分析［J］.同济大学学报，2003，31 (1):1-5.Luo Yong-feng，Yu Qing-xiang，Lu Yan，et al.Nonlinear analysis of supporting tensegrity structure for reflector of large radio telescope［J］.Journal of Tongji University，2003，31(1):1-5.

［10］ Leonhardt F，Schlaich J.Structural design of roofs over the sports arenas for the 1972 Olympic Games:some problems of prestressed cable net structures［J］.The Structural Engineer，1972，50(3):113-119.

［11］ Raid K.Some modeling aspects in the nonlinear finite element analysis of cable supported bridges［J］.Computer and Structures，1999，71(4):397-421.

［12］ Zi B，Duan B Y，Du J L，et al.Dynamic modeling and active control of a cable-suspended parallel robot［J］.Mechatronics，2008，18(1):1-12.

［13］ 袁亚湘，孙文瑜.最优化理论与方法［M］.北京:科学出版社，1997.