多核多线程并行求解线性方程组

冯 佩， 钟 诚， 韦 伟

(广西大学计算机与电子信息学院，广西南宁 530004)

0 引 言

线性方程组的求解是数值代数的基本问题之一，许多工程与科学计算问题最终都可归结为求解大规模线性代数方程组[1]。Gauss-Seidel算法是求解线性方程组的一种经典方法，它由Jacobi算法演化而来[2]。已有的求解线性方程组的Gauss-Seidel并行算法大多是基于SIMD模型或者M IMD-SM模型设计的[3-5]，并且针对的是方程组的系数矩阵，是稀疏矩阵的情形[6]，而对于大规模的矩阵求解可能会造成额外的同步开销或通信开销。基于多核处理器和FPGA混合结构的系统[7]，近年来已成为一种新型的计算平台。与单核处理器相比，多核处理器能够提供更强的并行处理能力，支持线程级并行和缓存高效[8，9]。

本文充分利用多核处理器的多级存储结构和多线程并行技术，研究在多核计算机上设计实现存储高效、可扩展的并行求解n阶线性方程组的Gauss-Seidel算法，并与已有算法进行实验性能对比。

1 增广矩阵的存储方式

设线性方程组A X=B，系数矩阵为A，增广矩阵为(A|B)，方程可以表示为:

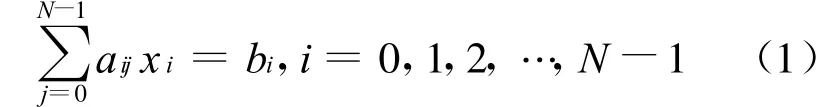
求解n阶线性方程组Gauss-Seidel算法的计算方法[10]如下:

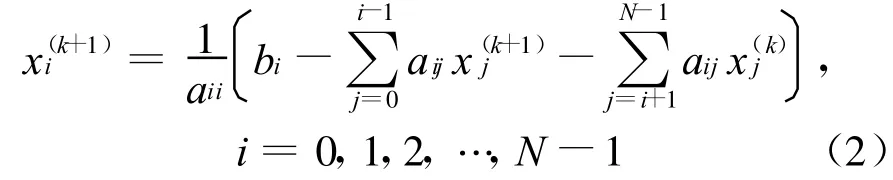
设矩阵规模为A N×N，共享L2Cache的大小为C2，私有L1Cache的大小为C1，处理核数目为p。根据多核计算机的多级存储层次，将增广矩阵(A|B)按行划分的方法如下:

(1)将主存中的N行矩阵数据依据L2Cache的大小进行分组，计算出每组中矩阵的行数。

对主存中数据进行分组时，假设主存中每组的大小为αC2，则可将主存分成组，其中N(N+ 1)为增广矩阵(A|B)中元素个数;α为L2Cache的利用率(α=0.6，0.7，0.8，0.9)。

记每组中的行数为L，每组中有L(N+1)个元素，则

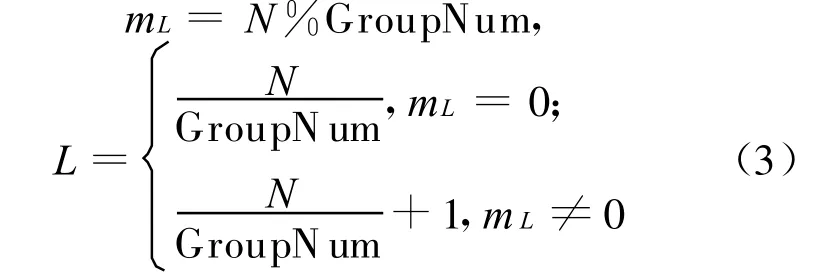
(2)对每组中的L行矩阵数据进行分块，并计算出每块中的矩阵规模。

假设每个L1Cache的可用大小为βC1，则每块的大小不超过 pβC1，β为 L1Cache的利用率(β=0.5，0.6，0.7，0.8，0.9，1.0)。记每块中的行数为n，每块中有n(N+1)个元素，则

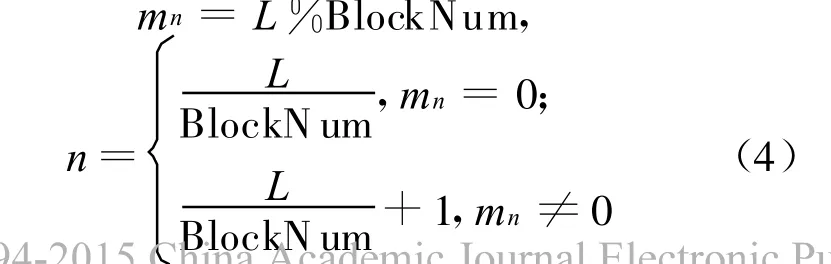
(3)将每块中的n行矩阵数据进行分段，并计算出每段中矩阵规模。

记每段的行数为S，每段中有S(N+1)个元素，则

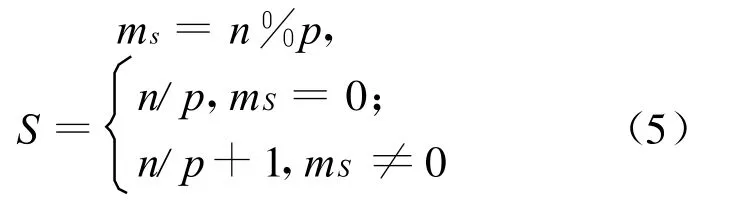
2 算法的设计与分析

设多核计算机有p个处理核，old[1，…，N]和new[1，…，N]分别用来存放旧的数据值和当前计算出的新值，c[1，…，N]存放新旧数据值的比较结果。

多核多线程并行求解n阶线性方程组算法的基本设计思想如下:

(1)并行地将初值赋给2个共享数old[1，…，N]和new[1，…，N]。

(2)按行划分方式将增广矩阵(A|B)进行分块，计算出分配到每个处理核的行数目以及这些行在每组、每块、每段中的位置，确定出各个处理核中每段的行在整个增广矩阵(A|B)中的开始和结束位置。

(3)p个处理核并行地计算每段中的矩阵行。

(4)根据下标对当前值和旧值求差的绝对值，并存放在共享数组c[1，…，N]中。

(5)重复执行步骤(3)、(4)，直到将每组、每块、每段中的行数全部计算出新值为止。

由于算法在执行过程中可能有不止一个处理核读取old[1，…，N]的值，而本文实验使用的多核计算机是支持并发读的，处理核只需要通过自己所要计算的行的下标读取old[1，…，N]数组中的值。因此，该算法第(1)步中并行赋初值所需时间复杂度为O(1)，第(2)步中计算划分后的矩阵块在每组、每块、每段中的位置所需的时间复杂度为:

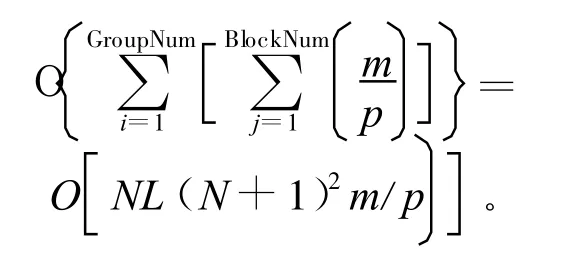
第(1)～(5)步所需的时间复杂度为:

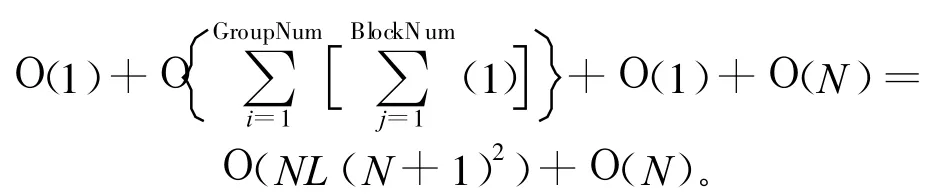
算法总的时间复杂度为:

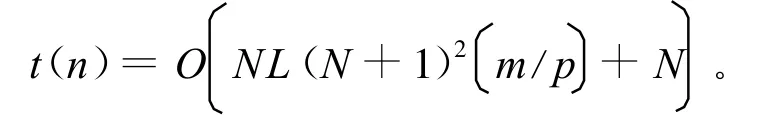
从(2)式可以看出，第k+1次迭代必须依次求出 x0k+1，x1k+1，x2k+1，…，xn-1k+1，计算过程具有较强的顺序性。当j＜i时，必须等待的计算完成后才能进行计算，这将会导致较大的同步开销;而且各个处理核在并行执行时相互之间存在数据移动，即处理核之间要相互访问，容易造成较大的通信开销。

为了减少同步等待，本文采用异步并行执行方式，将方程组的增广矩阵按多级存储方式存储到p个处理核的L1Cache中，p个处理核并行地对各自分配到的矩阵行进行计算，同时充分利用共享的L2Cache，使得处理核之间不存在数据移动，可大大减少通信开销，因此多核多线程并行求解线性方程组算法的运行速度比原Gauss-Seidel并行算法更快。

3 实 验

3.1 实验环境

实验多核计算机硬件平台为主存容量2 GB、二级缓存容量12 GB、每个处理器核心的一级缓存容量32 kB的Intel(R)Xeon(R)E5405 2.0 GH z4核计算机，在 Red Hat Enterprise Linux 5操作系统支持下，采用OpenMP和C语言编程实现多核多线程并行求解n阶线性方程组算法。

3.2 方程组系数矩阵

采用的方程组系数矩阵A和向量B为:

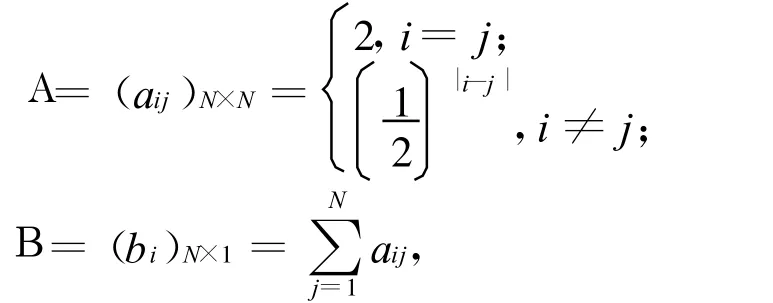
其中，i，j=1，2，…，N。实验中采用 x-0[i]初值为零向量，精度ε=0.01。

3.3 实验结果与分析

在拥有4个处理核的计算机上，使用动态关闭处理核的方法，本文采用不同矩阵规模、不同处理核数目、不同线程数目，分别测试并行求解线性方程组算法的运行时间、加速比和可扩展性;测试了二级缓存的利用率对算法性能的影响，并且将本文给出的多核多线程并行求解n阶线性方程组算法和原Gauss-Seidel并行算法进行了对比。

图1所示给出了阶数为600、1 000、2 000、3 000和3 500，分别在单机多核计算机上处理核数为4核、3核、2核运行时，随着线程数目逐渐增加，本文的并行求解线性方程组算法所需的运行时间。

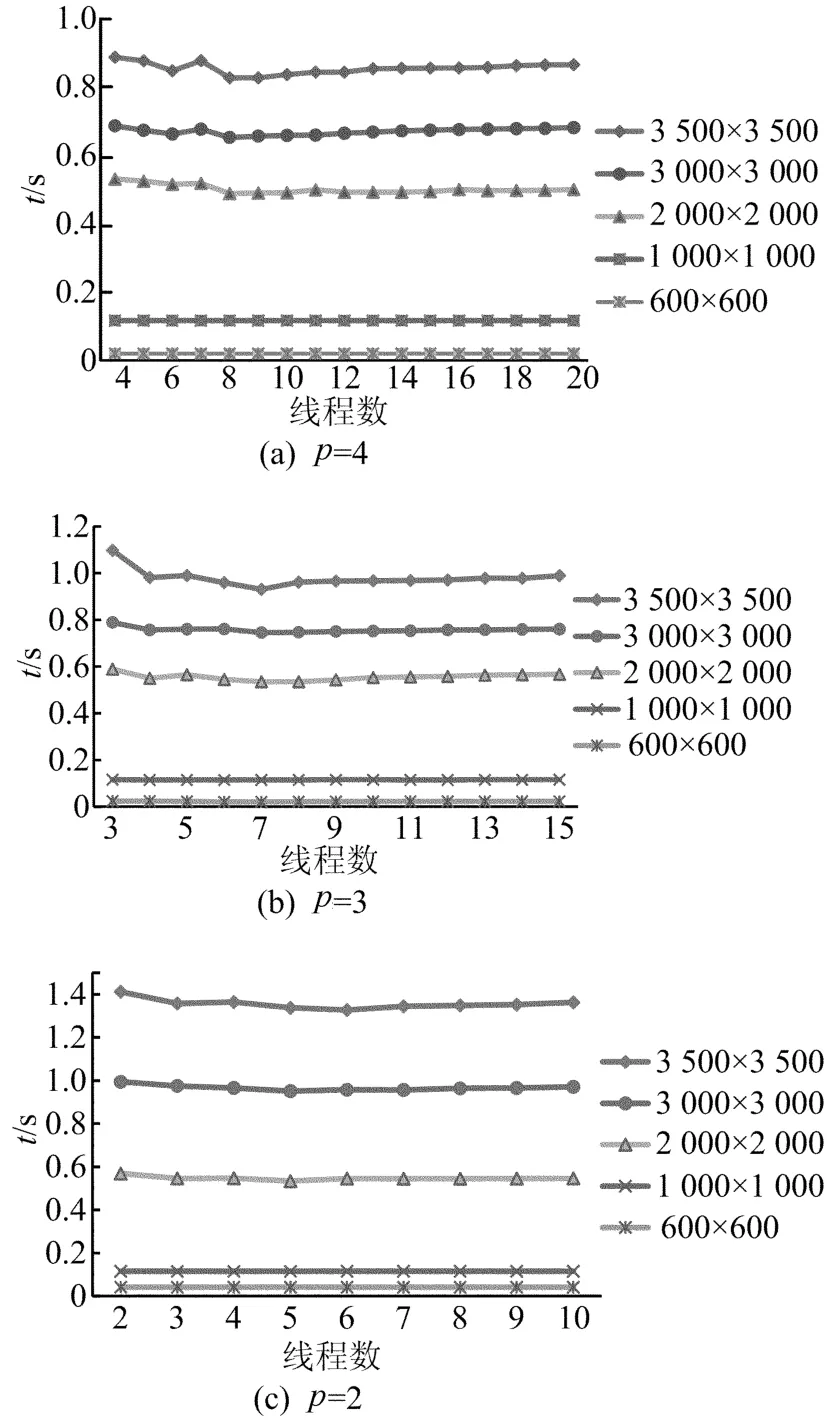
图1 本文算法在不同核数上的运行时间

图1的实验结果表明，运行不同处理核数目，随着线程数目的改变，本文给出的并行求解线性方程组算法的运行时间各不相同;同时也可以看出，对于不同处理核数，其最优线程数目也不同，一般均为处理核数目的2～3倍左右。当线程数目超过最优线程数时，算法的运行时间会上升，这是因为当线程数目增加时，会造成线程对处理器核的竞争，同时线程的启/停以及上下文切换也会增加一些额外的时间开销。

通过图1的对比也可以看出，随着线程数目的变化，线性方程组矩阵规模越大，算法运行时间变化幅度越明显，这是因为线性方程组矩阵规模较大时，算法对缓存的利用率提高，进而提升本文给出的并行求解线性方程组算法的效率。

不同矩阵规模，随着处理核数增加，采用最优的线程数运行时，本文算法的加速比和等效率曲线，如图2所示。

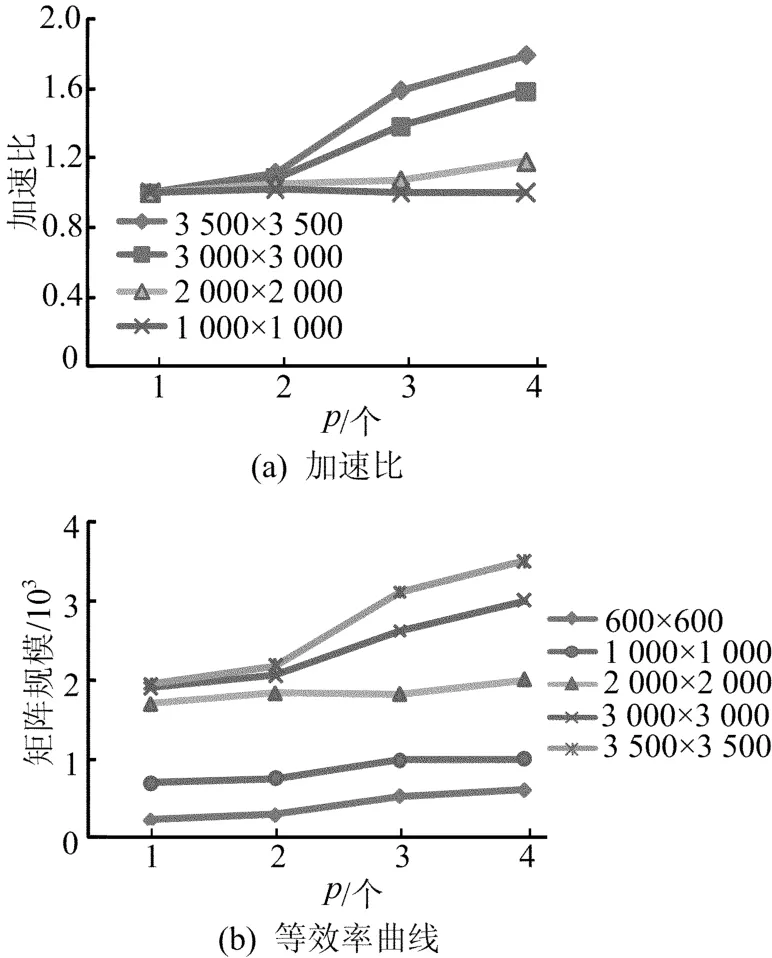
图2 本文算法的加速比和等效率曲线

图2a给出了随着处理核数的增加，不同矩阵规模采用最佳线程数运行时，本文算法并行求解方程组所获得的加速比。图2a的实验结果表明，采用最优的线程数，随着处理核数的增多，运行不同规模的线性方程组矩阵，本文给出的并行求解线性方程组Gauss-Seidel算法的加速比会略有增加，线性方程组矩阵规模越大，加速比的增加幅度越明显。

图2b的实验结果表明，当处理核数固定时，并行算法效率随着线性方程组矩阵规模增大而增大，处理核数越多，效率变化趋势越明显;同时可以看出当并行执行效率不变时，矩阵规模随着处理核数的增加而亚线性增加，这说明本文提出的多核多线程并行求解线性方程组算法是可扩展的。

运行4个处理核，不同矩阵规模下，L2Cache利用率增加时，本文算法所需的时间如图3所示。

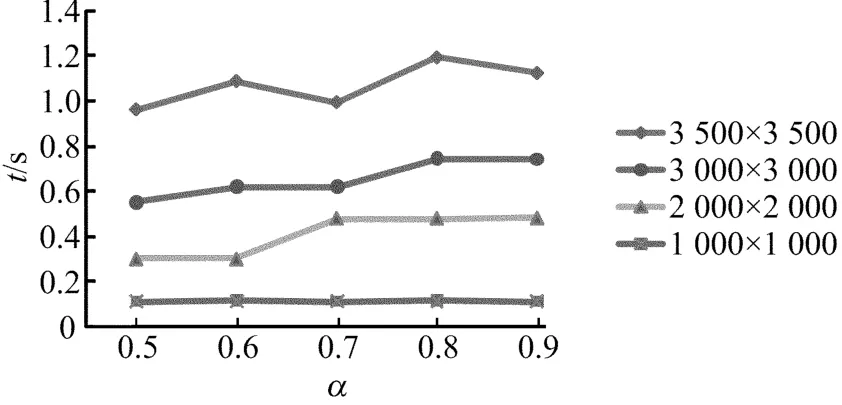
图3 L2Cacheα增加时本文算法所需时间

图3的实验结果表明，L2Cache的不同利用率，对算法性能有一定影响。当运行4个处理核时，对于不同规模的线性方程组矩阵，从整体上来看，当L2Cache的利用率α=0.5时，也即使用二级缓存容量的1/2时，本文给出的并行求解线性方程组Gauss-Seidel算法获得的效果最佳。由此可以看出，选择合适的缓存大小，合理地利用缓存，对并行求解线性方程组算法的性能会有所改善。

运行4个处理核，不同矩阵规模下，本文算法和原Gauss-Seidel并行算法的时间对比，如图4所示。

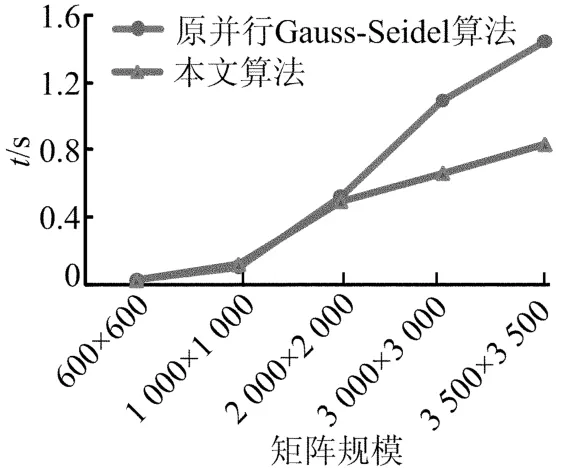
图4 本文算法和原Gauss-Seidel并行算法时间对比

图4的实验结果表明，当线性方程组矩阵规模较小时，原Gauss-Seidel并行算法的执行时间和本文给出的并行求解线性方程组算法的执行时间相当，但当矩阵规模增大时，本文算法的执行时间明显少于原Gauss-Seidel并行算法。这说明，当矩阵规模较大时，在多核计算机上运行本文的并行求解线性方程组算法更有效。

4 结束语

本文将线性方程组的增广矩阵按行进行分块并存储在多核计算机各级缓存中，多个处理核并行执行多线程对各段的矩阵行进行处理，设计实现了高效、可扩展的线程级并行求解线性方程组Gauss-Seidel算法，并通过实验测试获得不同的增广矩阵规模、运行处理核数和并行线程数目的最佳匹配关系以及各级缓存利用的最佳方案。

下一步的研究工作将在同构/异构多核机群系统上，研究设计存储高效、通信高效、加速比高、可扩展性好、进程级和线程级并行的线性方程组求解算法。

本文初稿首次刊登于《计算机技术与应用进展◦2010》

[1] 尚月强，杨一都.基于PVM的稠密线性方程组网上并行求解[J].计算机工程与设计，2006，7(9):1591-1594.

[2] Salkuyeh D K.Generalized Jacobiand Gauss-Seidelmethods for solving linear system[J].Jou rnal ofAp plied Mathematicsand Computing，1998，5(2):341-349.

[3] Malek M.Undirected graphsmodels for system-level fau lt diagnosis[C]//Pro ceedingsof 7th Symposium on Com pu ter A rchitectures，1980:1-35.

[4] BianchiniR P，BuskensW.Implemen tation of online distribu ted sy stem-level diagnosis theory[J].IEEE T ransactions on Compu ters，1992，41(3):616-625.

[5] K rzy sztof D，And rzej P.G lobally optimal diagnosis in systems with random fau lts[J].IEEE T ransactions on Compu ter，1997，46(2):200-204.

[6] 李晓梅，蒋增荣.并行算法[M].长沙:湖南科学技术出版社，2001:7-54.

[7] 胡文彬，吴剑旗，洪 一.多FPGA验证平台引脚限制的解决方案[J].合肥工业大学学报:自然科学版，2010，33(10): 1519-1522.

[8] Akhter S，Roberts J.Mu lti-core programm ing:increasing performance through softw are mu lti-threading[M].北京:电子工业出版社，2007:21-71.

[9] 周伟明.多核计算与程序设计[M].武汉:华中科技大学出版社，2009:4-124.

[10] 陈国良.并行算法的设计与分析[M].第3版.北京:高等教育出版社，2009:411-475.