基于RTK GPS系统的结构安全监测系统研究
王人鹏,姚连璧,孟晓林
(1.同济大学建筑工程系,上海 200092;2.同济大学测量与国土信息工程系,上海 200092;3.诺丁汉大学,英国诺丁汉)
基于RTK GPS系统的结构安全监测系统研究
王人鹏1,姚连璧2,孟晓林3
(1.同济大学建筑工程系,上海 200092;2.同济大学测量与国土信息工程系,上海 200092;3.诺丁汉大学,英国诺丁汉)
利用GPS系统在线监测获取的大量结构响应数据,完成了大量数据处理工作,得到了结构响应的时间序列。在此基础上,完成了结构响应的谱分析,初步建立了结构响应的状态空间模型及ARMA(autoregressive moving average method)模型。计算分析结果与大桥通车试验的实测结果及有限元模型预测结果相当吻合。研究表明,基于结构响应的状态空间模型及ARMA模型是评估结构动力性能的有力工具,同时进一步验证了通过RTK GPS系统建立结构安全监测系统的可能性。
RTK GPS系统;时间序列;状态空间模型;ARMA模型;有限元模型
1 前言
在南浦大桥的在线观测试验中,通过GPS接收机得到的观测信号,经过专门的处理分析计算,可以得到测点的空间位置信息。关于RTK GPS(realtime kinematic global positioning system)技术参见文献[1]。由于连续在线观测,实际可以得到每个测点连续的结构响应序列,即桥梁坐标系下测点的坐标时间序列。这些响应数据是实现结构安全评估的基础数据,隐含着丰富的力学信息。结构响应可以使用状态空间模型及ARMA模型比较深入地描述。其中ARMA模型可以推广为向量形式的ARMA模型即ARMAV(autoregressive moving average rector method)模型。结构安全监测的目标就是通过对结构系统输出信号的计算分析,识别结构系统的力学特征及力学参数,用于预测结构安全状况及完成结构性能的安全评估。
一般情况下,结构系统的动力学过程可以使用一组二阶线性微分方程组描述,即结构系统的动力学方程,该微分方程组可以变换为标准的状态空间方程形式。现代控制理论对线性系统的状态空间方程已经有了许多深刻的理论结果[2~6]。在结构系统的状态空间理论中,针对结构系统的主要力学参数,即结构自然频率、结构阻尼,引入一系列结构动力学一般不涉及的重要概念,推导了一系列重要结论,它们对于结构试验、结构识别及结构在线监测都是非常重要的结果[3],构成了结构安全监测的理论基础。例如,状态空间理论引入了结构系统的极点概念。结构极点总是一对共轭复数,联系了两个最重要的结构参数即结构频率与结构阻尼[3]。状态空间理论引入了结构范数概念。在结构安全检测分析中,结构范数可以作为结构模态截取的依据,实现结构模型的自由度消减,同时可以作为结构安全或者结构破损的依据[3]。每个结构系统的状态空间方程都可以等价地由相应的ARMAV模型表示。同样每个ARMAV模型也可以等价为某一结构系统的状态空间方程[7]。笔者将以结构系统的状态空间理论及相应的ARMA模型为理论基础,初步完成有关结构响应序列的状态空间模型及ARMAV模型的建立及结构响应的谱分析。
2 测点时间序列
由GPS接收机得到的观测信号,经过专门的分析处理程序,可以得到测点的空间位置信息。通过连续在线观测,可以得到在选定参考坐标系下,每个测点在观测时间段内一系列时刻的空间坐标,即测点的坐标时间序列。在对南浦大桥连续在线观测试验中,通过大量数据处理工作,针对12个GPS测点,得到了每个测点在桥梁坐标系下每个观测时间段的三维坐标值,即36个坐标时间序列。由于采样间隔为0.1 s,观测时间为2 h,每个坐标时间序列含有大量的时间坐标数据。应当指出,在实施桥梁在线观测过程中,不可避免地出现某些观测点上观测信号的非正常中断。因此在2 h的时间段内,某些观测点的时间序列会出现时间间隔不连续现象,即某些时间段上不存在观测坐标数据。在后续的工作中,将采用选定的公共时间段进行有关的分析计算。
为叙述方便,对36个坐标时间序列采用下面的命名方式,如coord-8-24-2,其中coord表示坐标值,必要时三个空间坐标值分别记为xcoord,ycoord及zcoord。其中的第一个数字代表观测点的编号,该数值可以取为1,2,…,12;第二个数字代表观测日期,代表2006年9月21—24日4天观测日期;第三个数字代表观测时间段,1、2、3分别代表一天内的三个观测时间段,即 9:00—11:00、16:00—18:00、23:00—1:00。三个时间段分别代表了桥梁结构所受载荷状态的典型时间段。
由于坐标时间序列包含大量的数据,分析结果十分庞大,为节省篇幅,在文章的后续部分,仅给出某一很短时间段上的图形显示,用以说明分析计算结果。对2006年9月23日第二观测时段16:00—18:00内,时间长度为600 s(开始的GPS时间为548900 s),抽取36个坐标时间序列,形成36个600 s长的坐标时间序列。以此36个坐标时间序列作为结构状态空间模型及ARMA模型的系统输出(Multi-Output),完成有关结构动力响应分析及结构系统识别分析计算。此时36个结构系统的输出通道中x坐标、y坐标及z坐标分别记为3i-2,3i-1和 3i,其中 i=1,2,…,12。
对36个通道的坐标时间序列作如下处理:计算序列的平均值,然后时间序列减去序列平均值得到新的时间序列。这样得到的时间序列可以近似作为观测点附近结构的位移近似值。此外,将得到的各个时间序列分为两部分,一部分用深色表示,该部分数据用以建立结构响应的状态空间模型及ARMA模型;一部分用浅色表示,该部分数据用于状态空间模型及ARMA模型预测的结构响应的比较,即结构系统验证[2]。36个通道的时间序列图形,如图1所示。
由图1可知,即使在600 s的时间内,12个测点的坐标时间序列构成也非常复杂,表明桥梁结构在运营状态下的振动非常复杂。这与有限元模型预测的复杂结构振型将导致的复杂结构位移相当吻合。由各个测点的时间位移序列图可知,它们都表现了某种程度的随机性特征,应该是环境荷载的随机性导致。观测点4及9上的时间序列表现有些特别,位移近似值比较大。观测点2上的位移值与对称的观测点7的相应位移值比较,在一系列的时刻点上偏大。目前还无法确切判断这些偏大的位移值是否意味着结构在经历了十余年的运营之后,结构性能产生了不可逆转的变化,但倾向于结构已经发生了某种程度的变化。这些现象无疑应引起关注,需要做进一步的深入研究。
3 结构响应谱分析
结构响应包含丰富的结构信息,其中振动谱对了解结构动力性能具有基本意义。对36个结构位移时间序列,进行了大量谱分析计算。为节省篇幅,下面只给出典型测点对应的600 s长的坐标时间序列的谱分析结果,如图2所示。
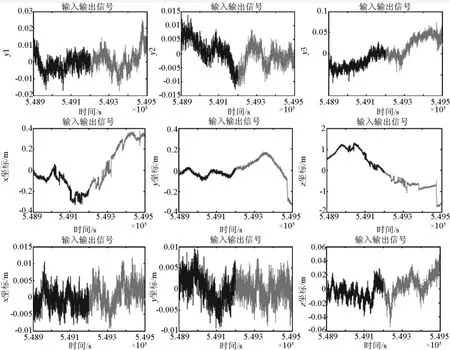
图1 测点1、4、8对应的x坐标序列、y坐标序列及z坐标序列(从左至右,从上到下)Fig.1 x-coordinate,y-coordinate,z-coordinate time series of 1,4,8 onitoring station points(arranged from left to right and from top to down)
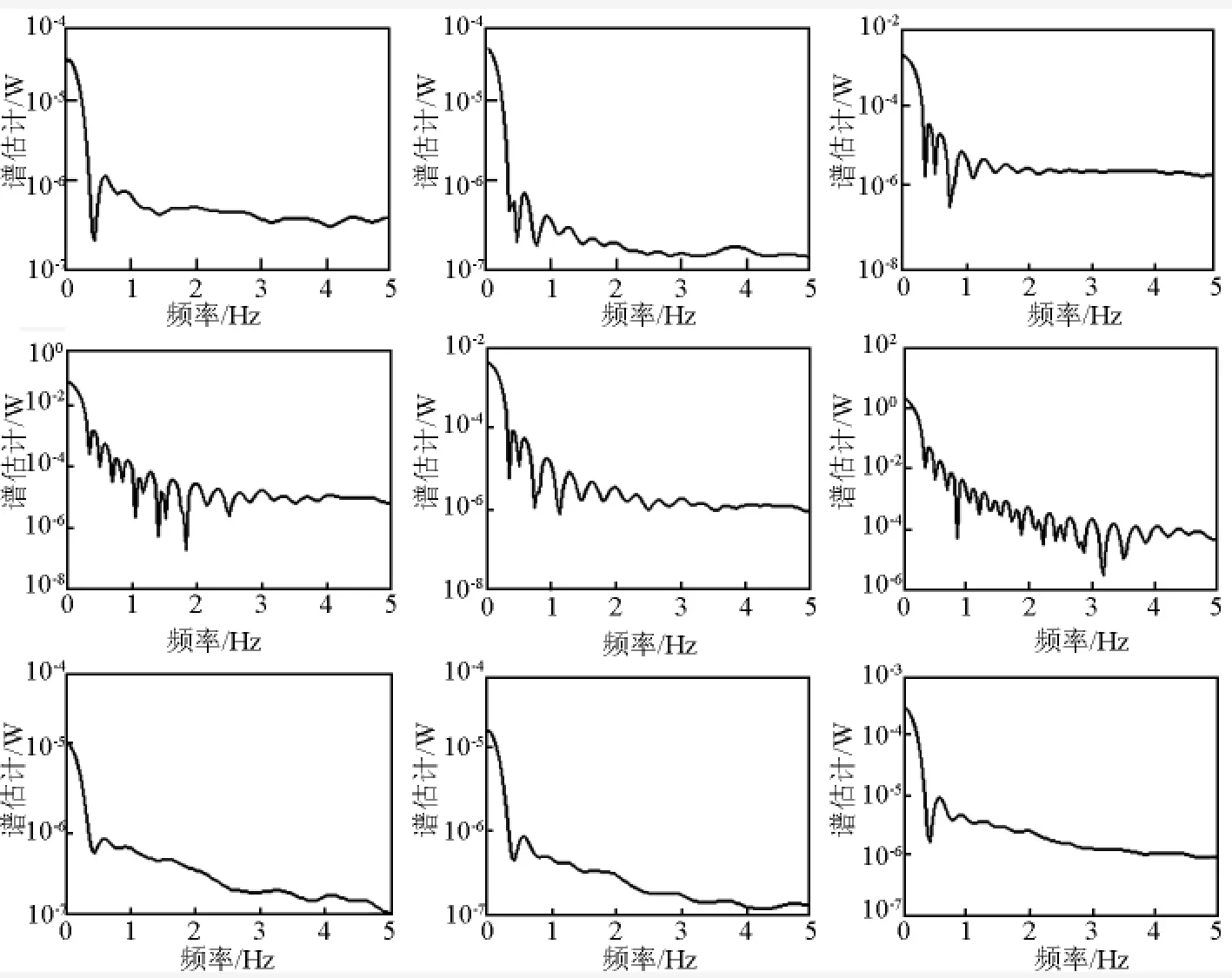
图2 测点1、4、8对应的x坐标序列、y坐标序列及z坐标序列的谱估计(从左至右,从上到下)Fig.2 Spectrum estimations for x-coordinate,y-coordinate,z-coordinate time series of 1,4,8monitoring station points(arranged from left to right and from top to down)
图2显示的结构响应信号所对应的频谱估计是通过Matlab的Spa函数得到的[8],已经通过光滑处理。为比较方便起见,下面列出了大桥通车试验实测频率,见表1[9],有限元模型预测的结构自然频率,见表2。从图1、图2可知,结构谱分析预测的振动频率集中在0~1.5 Hz,此范围之外的频率无法清晰获取。谱分析只能较好分离出对测点振动贡献最大的前若干阶频率,每个测点对应的谱估计都不尽相同,同一测点空间三个方向对应的谱估计也不尽相同,这反映了结构位移响应的空间分布的复杂性,也是对有限元模型预测的振型复杂空间分布的某种程度的验证。由谱分析得到自然频率的近似值,与大桥通车试验实测频率(见表1)及有限元模型预测的结构自然频率(见表2)都相当一致,有些信号得到的频率估计非常接近试验所得的频率及有限元模型预测的频率(如测点9的x坐标序列、y坐标序列的谱分析结果)。这从一个侧面检验了笔者得到的时间序列及相应谱分析的可靠性,由此也验证了结构动力特性的可分解性,即结构上任意点的结构响应包含了大量的结构动力响应特征,并且可以通过谱分析的方法得到结构的动力参数估计[3]。
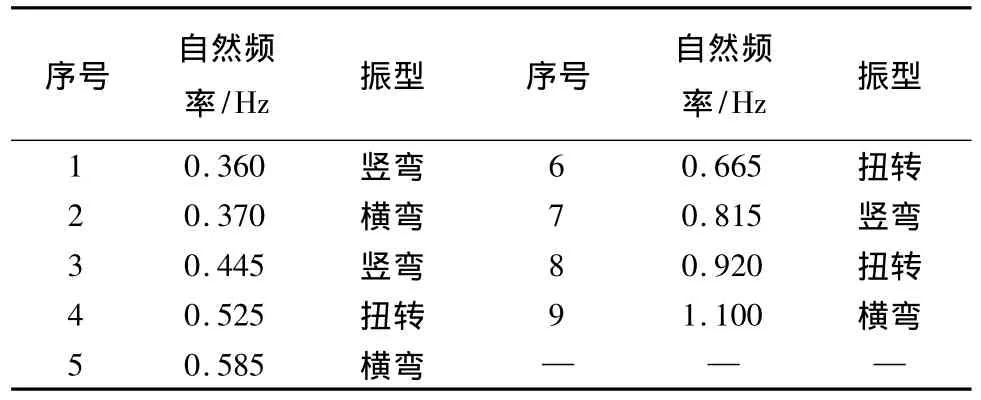
表1 南浦大桥全桥运营状态实测振动参数Table 1 Lower frequency measured by experiments
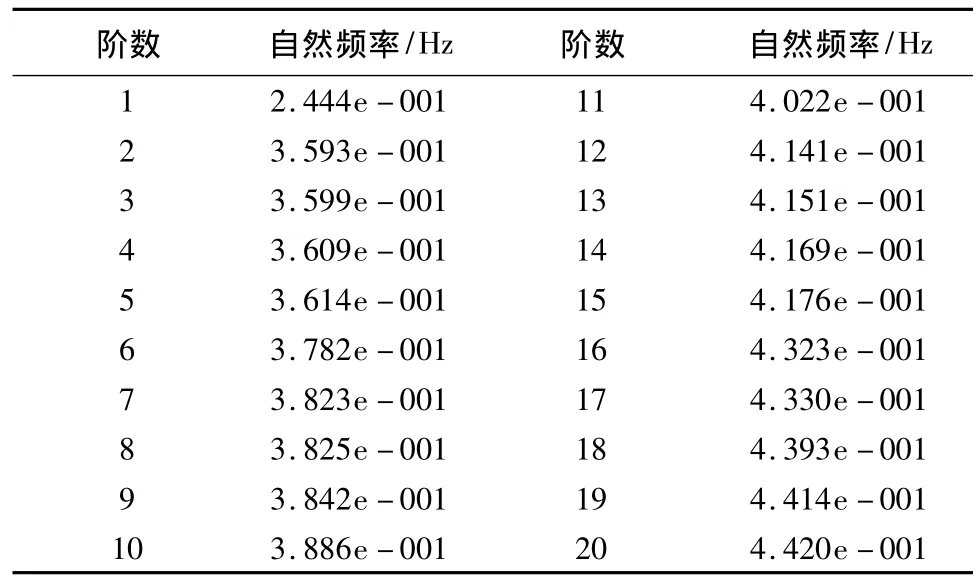
表2 南浦大桥结构有限元模型预测的20阶频率Table 2 First 20 order frequency predicted by finite element model
谱估计的方法有多种,笔者已对36个时间序列进行了各种谱分析计算,为了减少篇幅,下面只给出典型测点3、8、11、12所对应的z方向的各种谱分析结果,如图3所示。
从上述谱分析结果可知,同样的时间序列可以得到不同的谱分析结果。Blackman-Tukey方法可以比较清晰地分解出信号的频率分量,但会丢失一些频率分量;Frequency dependent resolution可以比较分解出更多信号的频率分量,但可能会额外分解出一些噪声频率;Empiricaltransferfunction可以比较分解出比第二种方法更多信号的频率分量,同时会额外分解出更多的噪声频率。为对结构响应做进一步的深入分析,需要研究各种谱分析理论,选择适宜的谱分析方法。
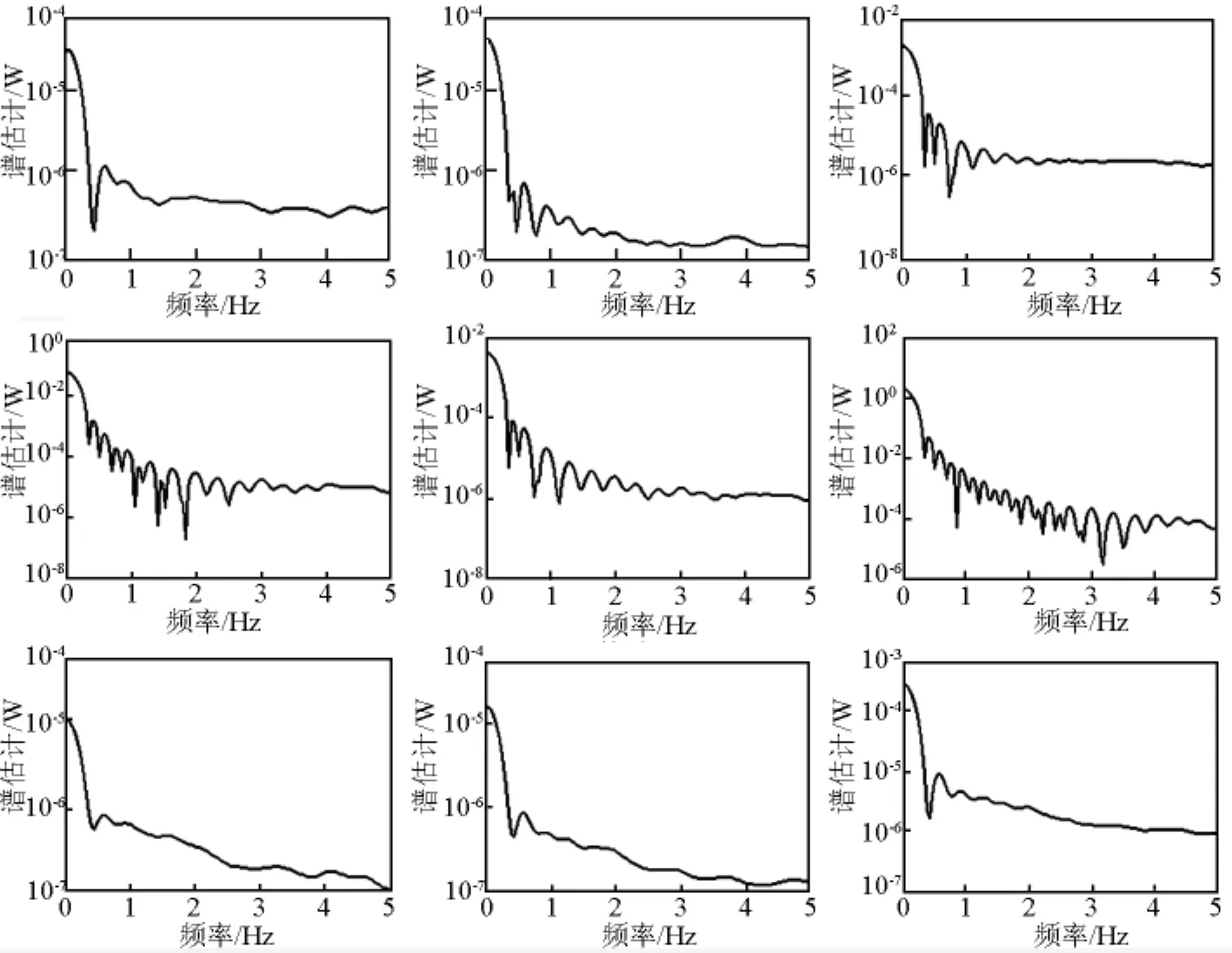
图3 测点3、8、11、12 z坐标序列对应的 Blackman-Tukey,Frequency dependent resolution及Empirical transfer function谱估计(从左至右,从上到下)Fig.3 Spectrum estimations for z-coordinate time series of 3,8,11,12 monitoring station points with Blackman-Tukey,Frequency dependent resolution,Empirical transfer function method(arranged from left to right and from top to down)
4 结构响应的状态空间模型及ARMA模型
由36个通道的结构响应信号,笔者初步建立了相应的状态空间模型及 ARMAV 模型[2,3,7,8]。状态空间模型及ARMAV模型的建立需要大量的计算资源,笔者已经完成了大量的建模计算。为了减少文章篇幅,下面只给出了利用上述时间长度600 s的36个坐标时间序列中的12个坐标时间序列,即3、8、11、12观测点的时间序列作为输出信号建立的结构响应的状态空间模型及ARMA模型。这些观测点都位于一些特殊空间位置,观测点3和8对应跨中位移,观测点11和12对应塔顶的位移,它们都应该具有较大弹性变形,因此测点z方向有较大的结构位移。下面以图形的方式,给出3、8、11测点z方向结构响应对应的状态空间模型的预测、极点和零点分布,如图4所示。
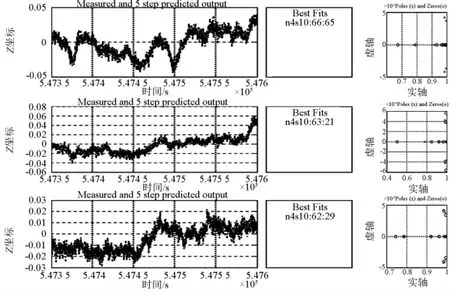
图4 测点3、8、11 z坐标序列对应的由12个输出、0个输入、10个状态变量、350个自由参数构成的状态空间模型的预测、极点和零点分布(从左至右,从上到下)Fig.4 Measured and simulated model output,poles and zeros of state space models which generated from z-coordinate time series of 3、8、11 monitoring station points with 12 outputs,0 input,10 states and 350 free parameters(arranged from left to right and from top to down)
图4中每一行对应一个测点的z坐标时间序列的状态空间模型的性能,每一行从左至右的第一幅图代表状态空间模型预测情况,其中深色代表实测信号,浅色代表预测信号;横坐标为采样时间,纵坐标为z坐标值。右侧小窗口的符号代表状态空间模型记号,数字代表预测精度。每一行的第二幅图是状态空间的零点及极点分布,其中横坐标为零点及极点的实部,纵坐标为零点及极点的虚部。极点是结构动力参数,自然频率及阻尼系数的复变函数[3]。极点模就是自然频率,极点转角的余弦就是阻尼系数。笔者认为结构响应的极点分布可以作为评估结构动力性能的一种方法,它们随时间变化的情况可能作为评估结构安全的一种指标。每一行的第三幅图是z方向输入信号对应的状态空间模型的跃阶响应(step response),其中横坐标为时间,纵坐标为状态空间模型的跃阶响应。状态空间模型是由输入输出信号、状态变量及结构参数决定的。以上分析结果选用了12个输出信号,即3、8、11、12测点的结构响应作为输出信号,由于无法测量结构载荷,因此选用0个输入信号,同时使用350个自由参数,建立了结构响应的状态空间模型。以下是采用了更多的自由参数(900个)建立的结构响应的状态空间模型,如图5所示。
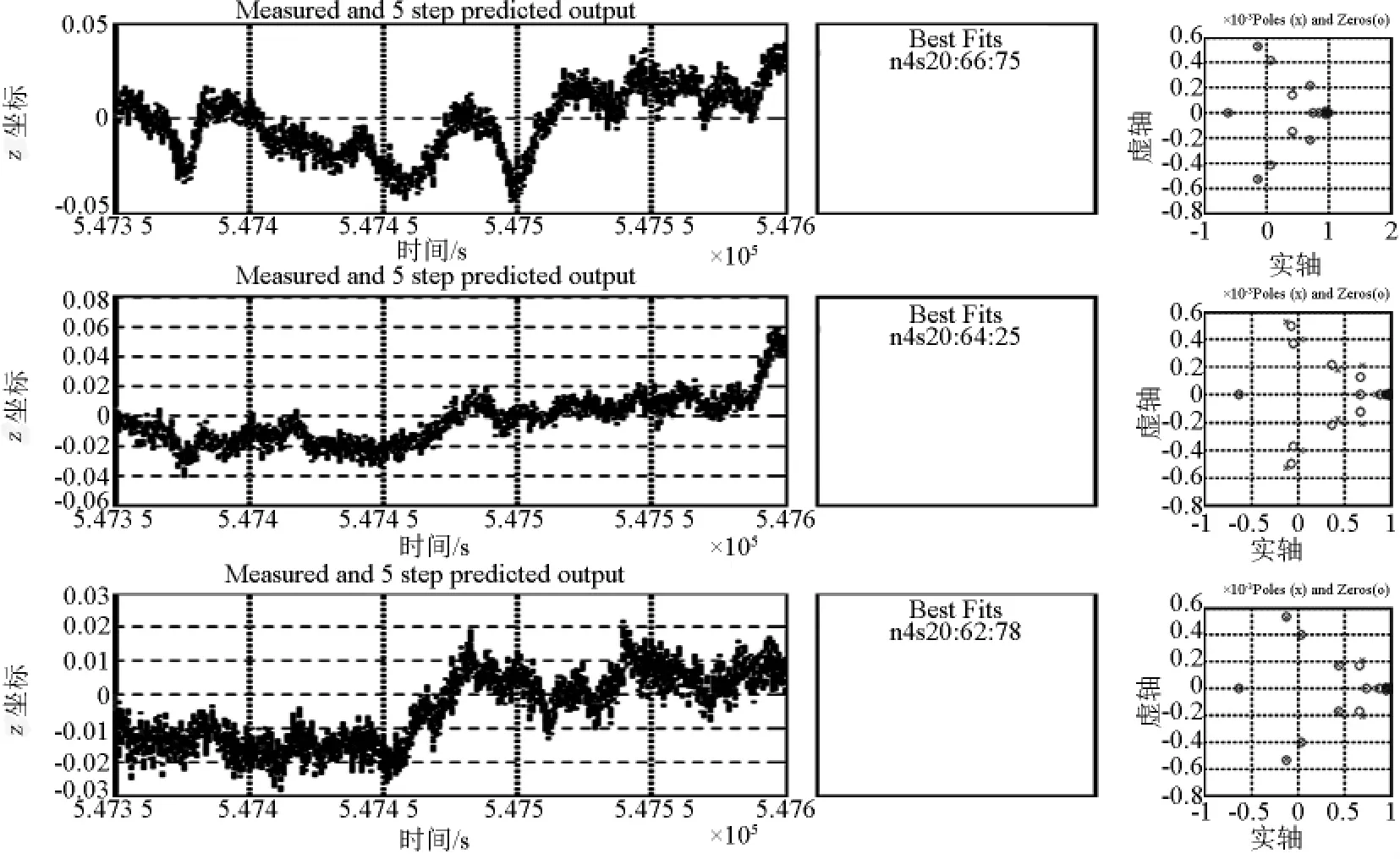
图5 测点3、8、11 z坐标序列对应的由12个输出、0个输入、20个状态变量、900个自由参数构成的状态空间模型的预测、极点和零点分布(从左至右,从上到下)Fig.5 Measured and simulated model output,poles and zeros of state space models which generated from z-coordinate time series of 3,8,11 monitoring station points with 12 outputs,0 input,20 states and 900 free parameters(arranged from left to right and from top to down)
图5的表示方法与图4相同。由图4和图5表示的状态空间模型的极点分布,同样可以得到结构自然频率和结构阻尼的近似估计。通过极点分布确认结构自然频率集中在0~1.0 Hz范围内。由极点推测的自然频率与谱分析推测的自然频率、大桥通车试验实测频率及有限元模型预测的结构自然频率(见表2)都相当吻合。比较上述两个状态空间模型可知,增加模型的阶数可以得到更精确的状态空间模型,即模型预测具有更好的精度。
图6是结构响应的ARMA模型,表示方法与图4相同。同样给出了3、8、11、12测点z方向时间位移序列对应的ARMA模型的预测、极点和零点分布,每行图形的安排与图4相同。
由图6表示的ARMA模型的极点分布,同样可以得到结构自然频率和结构阻尼的近似估计,与通过的状态空间模型得到的相应估计大体吻合。
对如何选择坐标时间序列以组成输出信号,存在数量极大的选择组合。算例只给出了4个测点在600 s时间长度内构成的时间序列的分析结果,实际观测数据的时间长度在20 h以上,数据量极为庞大,构成时间序列的选择组合也极为庞大。如何构成输出信号,以便建立有效的状态空间模型及ARMA模型是需要深入研究的课题。对笔者给出的计算分析结果,不是强调相关模型预测的精确度,而是强调这些结果的统计性质,因此没有列出具体的估计值。如果获取了结构在长期的正常工作状态下大量的结构响应数据,通过类似的大量的计算分析,完全能够得到结构响应的状态空间模型及ARMA模型中各类参数随时间变化的统计规律。例如,状态空间模型对应的极点及零点估计值的分布规律。笔者认为在结构性能发生了很大变化时,结构参数的统计属性应该同样发生较大变化,利用这些结构参数统计属性的变化可以预测结构破坏。因此这些结构性能参数的统计规律可以作为结构性能预测乃至结构破坏预测的计算指标之一。
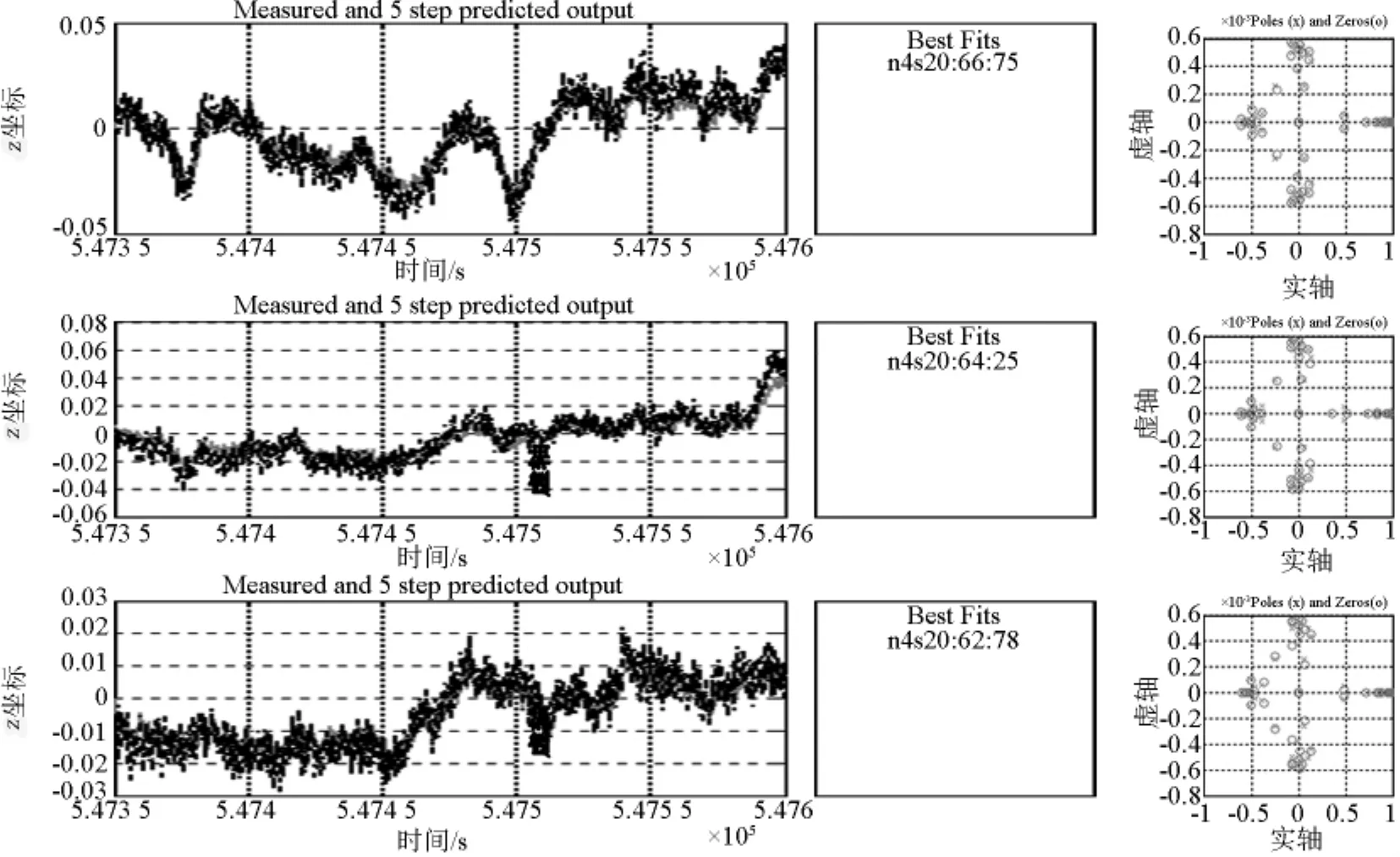
图6 测点3、8、11 z坐标序列对应的由12个输出、0个输入、576个自由参数构成的ARMA模型的预测、极点和零点分布(从左至右,从上到下)Fig.6 Measured and simulated model output,poles and zeros of ARMA model which generated from z-coordinate time series of 3,8,11monitoring station points with 12 outputs,0 input,20 states and 900 free parameters(arranged from left to right and from top to down)
5 结语
实现大型土木结构的安全监测及评估涉及复杂的结构状态空间理论、现代信号处理方法、系统识别、结构动力性能测试技术等多门交叉学科,实用的结构安全监测及评估系统还面临不少理论及实践的困难。研究表明在结构状态空间理论及现代信号处理方法的指导下,可以建立针对大型工程结构的结构安全监测及评估的理论基础和算法基础;通过基于RTK GPS技术的位移测量技术,可以构建基于RTK GPS系统的结构安全监测系统。
[1]Samama N.Global Positioning:Technologies and Performance[M].New York:Wiely,2008.
[2]Ljung L .System Identification[M].Sweden:Prentice Hall,Englewood Cliffs ,1987.
[3]Gawronski W.Advanced Structural Dynamics And Active Control of Structures[M].New York:Springer- Verlag,2004.
[4]Candy J V.Model- based Signal Processing[M].New York:Wiely,2006.
[5]Staffans O.Well- posed Linear System[M].New York:Cambridge University Press,2005.
[6]胡寿松.自动控制原理[M].北京:科学出版社,2005.
[7]Andersen P.Identification of civil structures using vector ARMA models[D].Denmark:Aalborg University,1997.
[8]MathWorks.Matlab System Identification Tools User Manual[M].USA:The MathWorks Incorporated,2007.
[9]同济大学桥梁实验室.南浦大桥主桥振动试验报告[R].上海:同济大学,1991.
Research on structural health monitoring(SHM)system based on RTK GPS system
Wang Renpeng1,Yao Lianbi2,Meng Xiaolin3
(1.Building Engineering Department,Tongji University,Shanghai 200092,China;2.Surveying and Geo-informatics Department,Tongji University,Shanghai 200092,China;3.The University of Nottingham,Nottingham,UK)
For the huge amount of raw data that were obtained during field data acquisition by the real-time kinematic global positioning system(RTK GPS)in structural health monitoring(SHM)system of the Nanpu Bridge in Shanghai,we finished lots of processing works and obtain x-coordinate ,y-coordinate,z-coordinate time series of all 12 monitoring station points.The coordinate time series were treated as the multi-outputs of the dynamic system and used to build the state space model and ARMA model and spectrum estimations for the response.The analysis results were consistent with the results of test that completed when the bridge was opened in 1990 and results that forecasted by fine finite element(FE)model.The research illustrated that the state-space model and ARMA model were efficient tools for evaluation of performance of civil structures,and furtherly proved the possibility of building the prototype SHM that based on RTK GPS.
RTK GPS system;time series;state-space model;ARMA model;finite element model
O241
A
1009-1742(2011)03-0063-08
2008-11-24;
2009-10-23
建设部专题项目“大型桥梁结构安全检测方法及系统研究”资助项目(20060909)
王人鹏(1964—),男,山西芮城县人,同济大学副教授,博士,主要从事结构数值分析方法及应用研究;E-mail:renpengwang@hotmail.com

