四阶Sigma-Delta微加速度计系统设计与分析

刘晓为，刘云涛，姜一鸣，尹 亮

(1.哈尔滨工业大学MEMS中心，150080哈尔滨，summer924@sina.com;2.哈尔滨工业大学微系统与微结构教育部重点实验室，150080哈尔滨;`3.哈尔滨工程大学信息与通信工程学院，150001哈尔滨)

高性能的微机械惯性传感器通常利用静电力反馈方式提高系统的线性度、带宽、动态范围［1］，反馈方式可分为模拟反馈和数字反馈.Sigma-Delta (ΣΔ)调制器是实现数字静电力反馈系统的最有效方式.相比于模拟反馈方式，ΣΔ调制技术可以提供直接的数字输出，采用一位数字反馈可以大大降低静电力非线性问题，更为重要的是这种方式消除了模拟反馈中由于质量块偏离严重而产生的静电力吸引问题，大大提高了系统可靠性［2］.

微加速度计的敏感结构可以看作质量－弹簧－阻尼的震动系统，并且具有二阶低通特性，因此如果把敏感结构包围在反馈环中，就起到了噪声整形的功能［3］.然而由于敏感结构部分非常低的直流增益，使得二阶ΣΔ结构很难实现低的量化噪声.为了获得高性能的ΣΔ微加速度计，近年来众多学者开始了高阶结构的研究和设计［4－6］.我国在该方面主要停留在模拟输出的接口电路研制上，未见数字加速度计的相关报导.本文建立了1个单环四阶ΣΔ微加速度计的系统模型，对该系统的稳定性、死区、空闲音进行了分析，并实现了传感器接口电路晶体管级的设计和流片测试，仿真和测试结果表明该加速度计具有良好的性能.

1 闭环ΣΔ微加速度计系统结构设计

本文所设计的闭环四阶ΣΔ微加速度计系统结构如图1所示，敏感结构具有二阶低通特性，其传输函数为

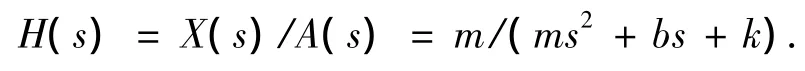
其中m为敏感结构质量块质量，b为阻尼系数，k为弹簧弹性系数.敏感结构将输入惯性力转换为质量块位移，Kdc为位移x到电容变化量的增益，表达式如下:

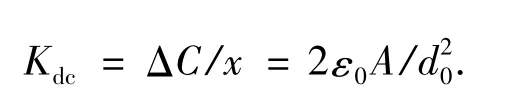
机械结构分子的热运动对系统引入了布朗噪声.电容变化量到前级电路输出电压的增益为

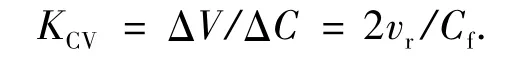
其中Cf为前级电容－电压转换电路的反馈电容.前级电路引入了电路噪声.前置补偿电路在高频部分引入部分相位偏移，从而使系统保持稳定.补偿电路的后面级联2个电学积分器，用以提供更好的噪声整形.具有高非线性度的一位量化器表示为可变增益Kq和白噪声源QN的组合.反馈通路采用2个一位DA转换，1个提供电学积分器的反馈电压，另1个为敏感质量块提供反馈力，使质量块保持在平衡位置，反馈电压到反馈力的系数为

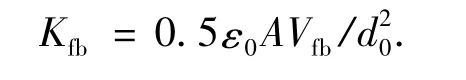
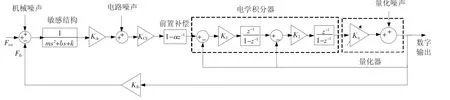
图1 四阶微机械ΣΔ加速度计系统

2 稳定性与参数优化

与ΣΔADC一样，在没有任何控制条件下，高阶ΣΔ微加速度计属于条件稳定，必须采取措施来保证四阶ΣΔ调制器的稳定性.由于量化器高非线性影响，使得高阶调制结构稳定性分析非常复杂，本文中将量化器看作可变增益与白噪声的组合，采用根轨迹法分析系统稳定性.

本文中所采取的相位补偿电路传输函数为

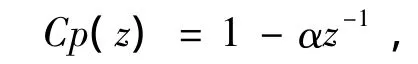
系统的开环传输函数决定了闭环系统的稳定性，根据图1，开环传输函数可表示为

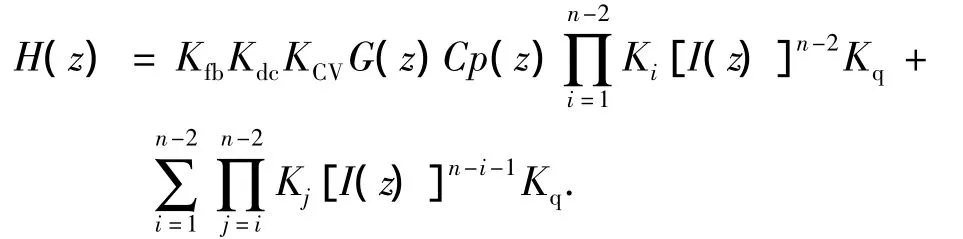
其中:I(z)为延迟积分器传输函数，I(z)= Z－1/(1－Z－1);n为调制器的阶数;Ki为电学积分器增益.根据经典控制理论，稳定闭环系统的所有特征根必须都在单位圆内.图2为该系统的根轨迹图，取α=0.6，K1=0.2，K2=0.5，由图2可知，当量化增益Kq非常高时，也就是量化器的输入信号很小，系统的1个特征根沿着负实轴离开单位圆，其余的极点对仍然在单位圆内，此时调制器内的信号开始增加，导致量化增益又开始下降，所以这个极点最终会移回单位圆，因此对于很大的Kq，系统产生的是1个稳定的极限环.当Kq＜0.003 42时，有一对极点离开单位圆，调制器信号会进一步增加，导致Kq进一步降低，而产生了不稳定的极限环.由仿真结果可知，只有当Kq＜0.003 42时，也就是量化器的输入信号非常高的时候才会使该系统不稳定.随着积分器增益的提高，系统稳定性逐渐变差，当2个积分器的增益都为1时，极点沿单位圆移动，系统任何微小的波动都可能导致系统进入不稳定状态.

α反映了系统的补偿深度，为了更清晰表明稳定性与补偿深度的关系，在S域重新绘制系统根轨迹图，图3为系统的根轨迹与α的关系，由此可见，随着α的增加，根轨迹逐渐由右半平面进入左半平面，使得稳定性逐步提高.

降低积分器增益可以提高系统稳定性，然而也会影响噪声整形能力，降低系统精度［7］.该系统的信号－噪声－谐波失真比(SNDR)与积分器增益关系如图4所示，由仿真结果可知，当α= 0.6，K1=0.6，K2=1时，即可以确保系统的稳定性，又得到了最高信噪比.

图2 系统根轨迹(α=0.6，K1=0.2，K2=0.5)

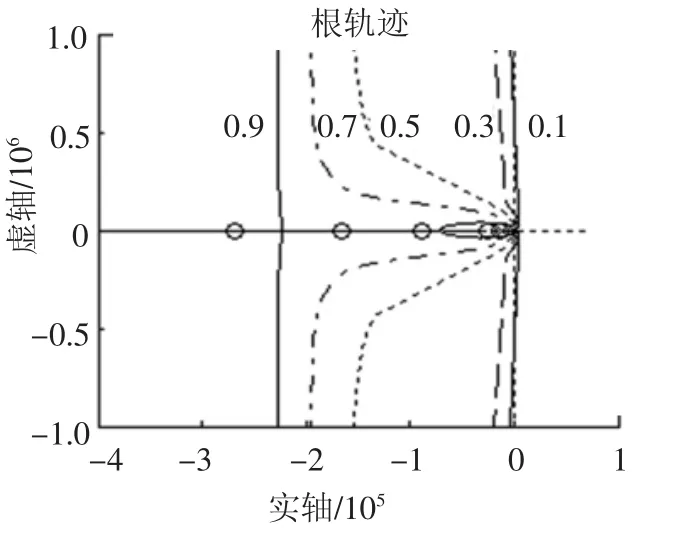
图3 稳定性与补偿程度的关系

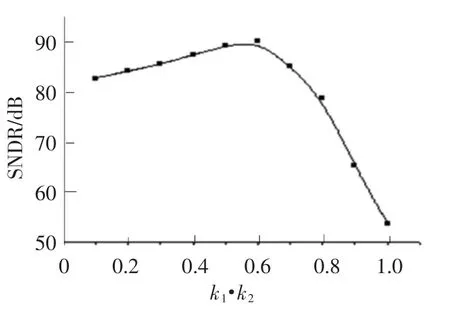
图4 SNDR与积分器增益关系

3 性能分析

在ΣΔ微机械加速度计中，影响系统精度的噪声主要有3种:布朗噪声、电路噪声和量化噪声.布朗噪声是由于热分子的无规则运动引起的，电路噪声主要包括前级放大器噪声、开关热噪声和参考电压噪声.量化噪声是在模拟到数字的转换过程中产生的［8］.根据图1所建立的系统模型可知，量化噪声受到敏感结构和二阶电学积分器的抑制，噪声整形能力依赖于敏感结构的直流增益和2个极点的位置，由于敏感结构直流增益非常低，导致其量化噪声整形能力远低于同阶数的电学积分器.若获得高的噪声整形能力，敏感结构需要同时具有极低的阻尼和弹性系数，不仅在工艺上难以实现，而且严重限制了传感器的机械带宽，因此在传感器的设计中要折中考虑带宽和量化噪声的关系.而且与仅采用敏感结构作为积分器的二阶ΣΔ调制器不同，高阶结构中机械噪声和电路噪声也同样受到了一定抑制.

敏感结构有限的谐振频率导致调制器的输出数字流中产生了1个死区，此时输出不再随输入而变化［9］.二阶微机械ΣΔ调制器中，死区的影响可能比其它任何噪声都要严重，这样死区就限制了该传感器能检测的最小加速度［10］.如果输入信号小于死区的临界值，在输出频谱上将看不到输入信号，调制器输出的数字码不能够反映输入信号.提高采样频率可以降低死区，但会增加电路噪声，功耗和电路设计难度.在高阶结构中，由于前向通路中的电积分器在低频部分提供了很高的增益，因此可以有效地降低死区，提高系统的检测分辨率.图5为所设计的四阶系统的功率谱密度，频率为30 Hz的正弦加速度信号，由图可见，该四阶微机械ΣΔ调制器中死区低于100 ng，因此在高阶结构的设计中，死区的影响可以被忽略.

图5 四阶ΣΔ加速度计输出频谱

在ΣΔ微加速度计中另外1个重要的影响就是空闲音.如果输入信号接近零时，数字反馈信号会使得敏感质量块以采样频率1/4的频率上下扰动，当输入信号频率非常低时，所产生的空闲音会折叠到基带中，而影响系统的信噪比.图5中可以看到由于额外的电积分器的作用，量化噪声被随机分布在整个频带内，从而消除了空闲音.

4 结果与讨论

四阶ΣΔ微加速度计的输出频谱如图6所示，输入为1 g、250 Hz正弦信号，在250 kHz采样频率、128倍过采样率(OSR)下，该系统的SNDR为90.7 dB，有效位(ENBO)为14.7位.并且由结果可知，500 Hz以内量化噪声低于1 μV/Hz1/2，因此在低频部分，量化噪声可以被忽略.

图6 四阶ΣΔ加速度计输出频谱

表1 加速度计系统测试结果

基于以上系统级的分析与讨论，实现了传感器接口电路晶体管级的设计和仿真，该电路采用0.5 μm 2层多晶2层金属CMOS工艺流片，制成ASIC芯片与传感器结构的双片集成微加速度计.开环模式下，采用HP 35670A动态信号分析仪测试系统的噪声水平，测试结果为开环噪声12 μg/Hz1/2.开环模式下，系统的噪声主要由前端的电容－电压转换电路限制，由于采用了低噪声运放及相关双采样技术，所设计的电路具有很低的电路噪声.闭环模式下，对输出数字信号进行采集，并利用Matlab进行频谱分析，测试结果为闭环噪声80 μg/Hz1/2.测试结果表明闭环噪声高于开环模式，这可能是因为随着输出数字高低电平的变化，反馈回质量块的反馈电压不断地在高低电压间转换，从而造成质量块受到的静电力不断变化而产生比较严重的扰动.另外，由于敏感结构的2个可变电容在无外加信号时不相等也会对输出产生一定的影响.在1 g状态下对传感器进行翻转实验，测试表明:该传感器的灵敏度为1.2 V/g，非线性度为0.2%.该加速度计系统级的测试结果如表1所示.

5 结论

本文完成了1个单环四阶ΣΔ微加速度计的系统级分析与设计，对系统的稳定性、噪声传递、死区及空闲音作了比较详细的分析，并在此基础上实现了传感器的加工制作，测试结果表明该微加速度计具有高灵敏度、小量程、低噪声的特点，具有广泛的应用前景.

［1］AALTONEN L，HALONEN K.Continuous-time interface for a micromachined capacitive accelerometer with NEA of 4 μg and bandwidth of 300 Hz［J］.Sensors and Actuators，2009，154:46－56.

［2］KULAH H，CHAE J，YAZDI N，et al.Noise analysis and characterization of a sigma-delta capacitive microaccelerometer［J］，IEEE Solid-State Circuits，2006，41 (2):352－361.

［3］GOMEZ J M，BOTA S A，MARCO S，et al.Force-balance interface circuit based on floating MOSFET capacitors for micro-machined capacitive accelerometers［J］.IEEE Transactions on Circuits and Systems，2006，53 (7):546－552.

［4］DONG Y，KRAFT M，WHITE W R.Higher order noise-shaping filters for high-performance micromachined accelerometers［J］.2007，56(5):1666－1674.

［5］AMINI B V，ABDOLVAND R，AYAZI F.A4.5 mW closedloop delta-sigma micro-gravity CMOS SOI accelerometer［J］.IEEE Solid-State Circuits，2006，41(12):2983－2991.

［6］PETKOV V P，BOSER B E.A fourth-order sigma-delta interface for micromachined inertial sensors［J］.IEEE Solid-State Circuits，2005，40(8):1602－1609.

［7］BAIRD R T，FIEZ T S.Stability analysis of high-order delta sigma modulation for ADC’s［J］.IEEE Transactions on Circuits and Systems，1994，41(1):59－62.

［8］LOLLAR M，MICHAELI L.Noise consideration for micromachined digital accelerometer［C］//Proceeding of IMTC.Sorrento:［s.n.］，2006:507－512.

［9］LEMKIN M，Micro accelerometer design with digital feedback control［D］.Berkeley:Dept Electrical Eng Comp Sci，Univ California Berkeley，1997.

［10］DONG Y，KRAFT M，GOLLASCH C，et al.A highperformance accelerometer with a fifth-order sigma-delta modulator［J］，Micromechanics and Microengineering，2005，15:22－29.