超空泡射弹尾部冲击载荷的仿真研究

张劲生，张嘉钟，魏英杰，王 聪

(哈尔滨工业大学航天学院，150001哈尔滨，zjn88@126.com)

当水下射弹的速度足够大时(≥50 m/s)，将产生超空泡现象，超空泡将弹体绝大部分表面与周围的水分隔开，仅头部与水接触.从而极大地降低了射弹所受的流体阻力.超空泡的出现也极大地改变了射弹的运动特性.由于发射时射弹所受的扰动，射弹在飞行时，还会绕着头部水平轴线在铅锤面内不断摆动.实验表明，随着摆动，射弹尾部与空泡壁面会连续地发生碰撞(尾拍).尾拍载荷对射弹的弹道特性、弹体的强度和运动稳定性都有重要的影响［1］.

由于超空泡射弹的特殊性:射弹内部空间小，使传感器的安装存在困难;极强的瞬态冲击载荷对传感器和测试系统又有潜在的破坏作用，因此用试验测试手段，来研究射弹的冲击载荷和结构响应的难度很大［2］.由于射弹尾拍冲击的瞬时性和复杂性，一些文献通过理论分析和数值计算，对射弹的动力学和振动特性进行研究时［3－6］，都是先对尾拍载荷进行高度的简化和假设.这样得到的载荷形式必然与实际存在较大的差别，同时，一些对尾拍载荷有重要影响的因素还没有被研究.

本文，利用Logvinovich G.V.的独立膨胀原理对液体域提出了一种简化处理模型，然后采用流固耦合分析的方法，对射弹尾拍冲击载荷进行仿真研究.分析了扰动角速度、射弹质量、刚度、和质心位置对冲击载荷的影响.

1 射弹结构模型与受力分析

射弹模型为平头圆锥体，长0.12 m，前端直径0.008 m，后端直径0.015 m.材料为钢，且只考虑弹性变形.

为简化计算，不考虑空泡内气体对弹体的阻力和弹体重力;弹体载荷包括前端面上的流体阻力FR和尾部的尾拍冲击力FI;在惯性作用下，弹体作减速飞行，同时发生尾拍.如图1所示.

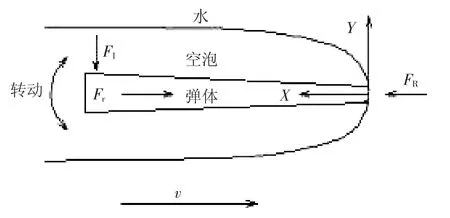
图1 射弹受力示意

FR方向沿模型轴向，其大小为［7］:FR= ρAcDv2/2，其中ρ、cD分别为流体的密度和阻力系数，A、v分别为模型前端面积和前进速度.模型的加速度a和惯性力FT由下式确定:

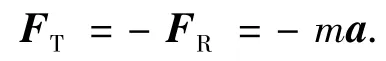
2 计算模型

2.1 流体域的简化计算模型

由于多相CFD计算及空化模型所带来的困难，对超空泡的非定常计算要耗费大量的计算时间，再加上空泡流与结构非线性振动的耦合作用，其计算耗时将是巨大的.本文提出的流体域简化计算模型，可以对射弹尾拍过程进行有效的数值模拟，同时还显著降低了计算的时间耗费.

对于超空泡射弹，根据Logvinovich G.V.的独立膨胀原理［8］，所有空泡横截面在其所在的平面内由空化器中心几乎独立地向外扩展，而在射弹飞行方向(纵向)上几乎没有速度，这已经为试验所证明［9］.同时考虑到尾拍的瞬时性，尾拍过程可以看作是运动着的弹体与静止的水面之间的拍击过程.也可以看作是，弹体模型做定轴转动时其尾部与高速前进的水面间的撞击过程.所以，通过圆筒形的运动流体来代替射弹周围的液体流动、用圆筒的内表面来代替空泡壁面(见图2 (a))，就完全可以模拟模型所受的撞击过程.

2.2 计算域与边界条件

流体域的长度0.74 m，内径0.022 m，外径0.2 m，其内径由超空泡半径的经验公式来确定［10］:

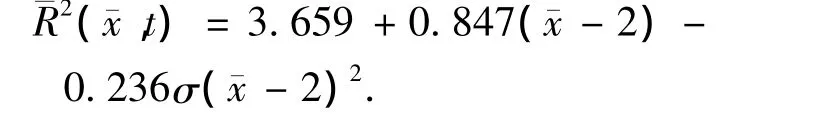
弹体模型的前端面中心点看作静止不动，在初始扰动角速度的作用下，模型绕该中心在铅垂面内做上下摆动，尾部与水平前进的流体域内表面不断发生碰撞.

由于对称性，流体域只取一半来计算.其边界条件为速度边界和对称边界(见图2(b))，边界速度(射弹速度)的变化区间取为300～1 000 m/s，边界速度大小随时间变化，并按下式确定［3］:

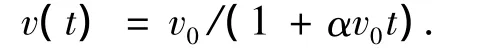
其中v0、α分别为射弹的初始速度和系统常数.

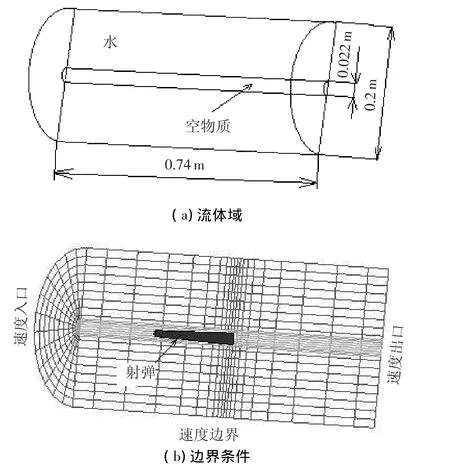
图2 LS-DYNA计算模型(半模型)

2.3 数值方法

弹体模型的大范围转动与其弹性变形相耦合，属于大转动非线性问题;同时弹体与水又发生流固耦合作用，这些都会对尾拍力产生重要影响.本文采用LS－DYNA软件进行仿真计算［11］.弹体模型采用全积分S/R六面体单元，其稳定性较好，可避免沙漏的产生，单元算法为拉格朗日算法.流体域采用中心单点积分的带空白材料的单物质ALE单元，由于忽略气体对弹体的作用，所以将气体设为空白材料，弹体单元仅与密度较大的流体(水)发生耦合作用，流体的输运采用二阶精度的Van Leer+HIS对流算法，并使用欧拉算法对整个流场进行CFD计算.弹体模型与流体间的耦合采用欧拉——拉格朗日耦合算法.单元网格采用六面体结构化网格，流体网格与弹体网格相互重叠，固体单元与流体单元之间采用无侵蚀的罚函数耦合方法，以实现力学参量的传递.为避免发生渗透现象对弹体尾部处的流体网格进行了局部加细.

3 计算结果与分析

射弹初始角速度大小是衡量扰动强度的重要因素，同时，射弹自身的重量、刚度、质心位置等，也会对尾拍冲击载荷的大小和作用时间产生影响.

3.1 尾拍载荷与初始角速度的关系

初始角速度ω分别为2、30、50、100、200和300 rad/m.对尾拍力的冲击次数n，力的幅值a，尾拍力的最大值A进行计算，得到图3所示的关系图.

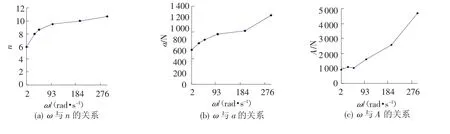
图3 初始角速度与尾拍载荷关系

从图中可以看出，由于ω的增加，使尾拍载荷的大小和作用频率都有增加的趋势;同时，由于弹体的动量矩随ω而增大，导致载荷最大值A明显增大，该最大值在首次碰撞时产生，然后很快衰减，见图4.

图4 尾拍载荷的变化

3.2 尾拍载荷与射弹质量的关系

对应于不同的质量，射弹的密度ρ分别取为3 000、5 000、7 000、9000和10 000 kg/m3.尾拍冲击的次数n、冲击作用时间τ、力的幅值a与ρ的关系如图5所示.弹体质量的增加将导致弹体惯性矩变大，从而使撞击时间变长、单位时间内碰撞次数降低;同时，撞击力的幅值也呈增大的趋势.

3.3 尾拍载荷与射弹刚度的关系

射弹弹性模量 E分别取为7×1010、9.6× 1010、2×1011、6×1011、8×1011、2×1012Pa.得到E与a的关系如图6所示.从图中可以看出，随着E的增加，冲击载荷的大小明显降低.

3.4 尾拍载荷与质心位置的关系

射弹质心到头部转动中心的距离lc分别取0.060～0.082 m间的一系列值，得到lc与尾拍载荷的n和τ的关系如图7所示.

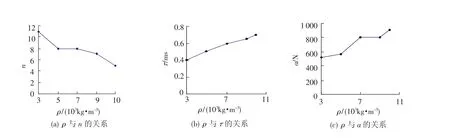
图5 弹体密度与尾拍载荷关系

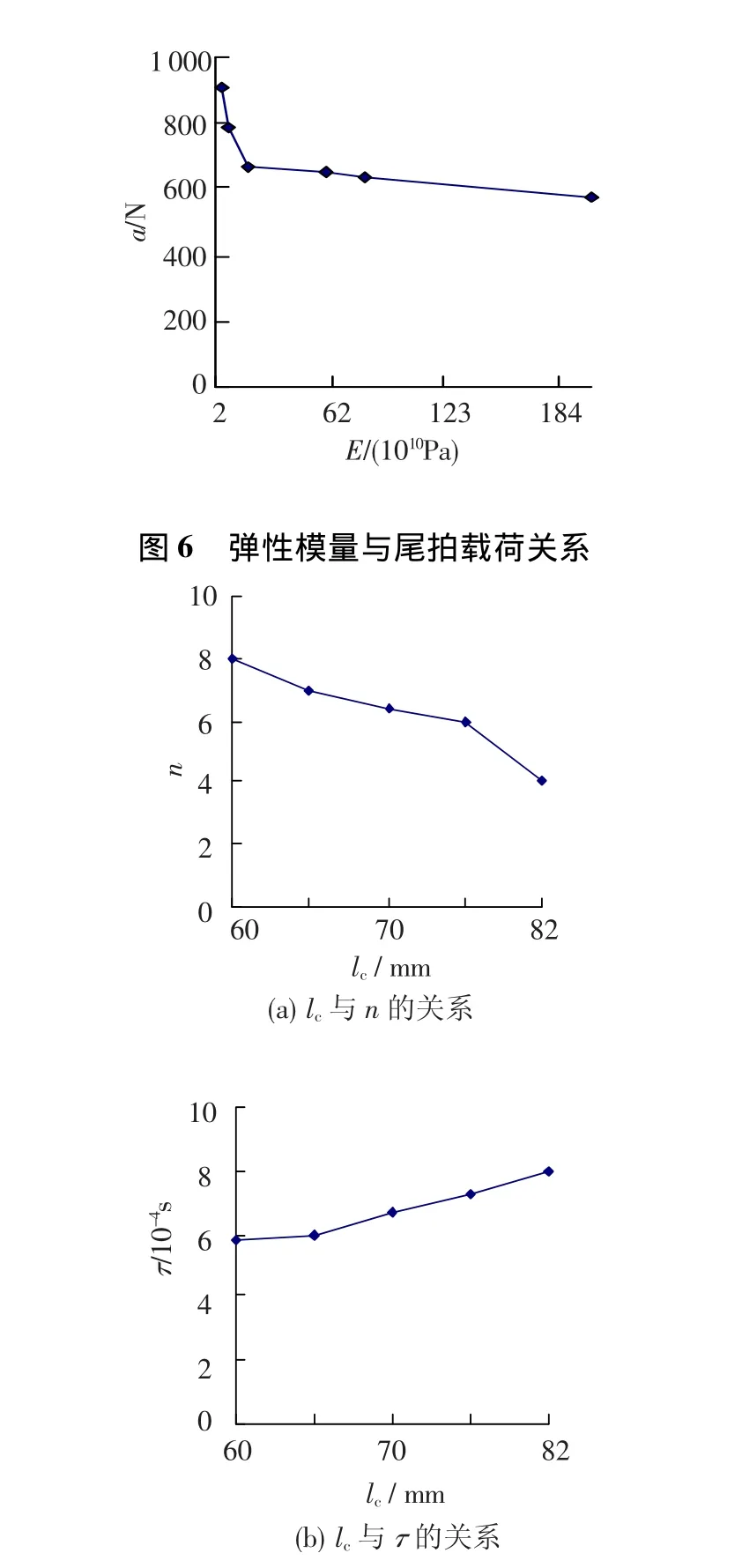
图7 质心位置与尾拍载荷关系

可以看出，质心距离lc的增加也会使撞击时间变长、单位时间内碰撞次数降低.

4 结论

1)初始扰动角速度和弹体质量的增加都会使尾拍力增大，而弹体弹性模量的增加会使尾拍力变小.

2)相同时间内，尾拍碰撞次数随初始角速度的增加而增多，随弹体质量的增加和质心的后移而减少;一次撞击的作用时间随着质量的增加和质心的后移而变大.

3)为减小尾拍冲击力对射弹结构和运动稳定性可能产生的破坏作用，应减小初始扰动角速度，并综合考虑弹体密度、刚度和质量分步的影响，从而降低尾拍冲击力的强度和频率.

［1］曹伟，魏英杰，王聪，等.超空泡技术现状、问题与应用［J］.力学进展，2006，36(4):571－579.

［2］吴三灵，温波，于永强，等.火炮动力学实验［M］.北京:国防工业出版社，2004:92－100.

［3］RAND R，PRATAP R，RAMANI D.Impact dynamics of a supercavitating underwater projectile［C］//Proceedings of the 1997 ASME Design Engineering Technical Conferences.Sacramento:ASME，1997，DETC97/VIB－3929.

［4］KULKARNI S S，PRATAP R.Studies on the dynamics of a supercavitating projectile［J］.Applied Mathematical Modelling，2000(24):113－129.

［5］RUZZENE M，SORANNA F.Impact dynamics of elastic supercavitating underwater vehicles［C］//9th AIAA/ ISSMO Symposium on Multidisciplinary Analysis and Optimization.Atlanta:AIAA，2002:1－11.

［6］孟庆昌，张志宏，顾建农，等，超空泡射弹尾拍分析与计算［J］.爆炸与冲击，2009，29(1):57－60.

［7］KIRSCHNER I N，KRING D C，STOKES A W，et al. Control strategies for supercavitating vehicles［J］.Journal of Vibration and Control，2002(8):219－242.

［8］VASIN A D.The principle of independence of the cavity sections expansion(Logvinovich’s Principle)as the basis for investigation on cavitation flows［C］//RTO AVT Lecture Series on“Supercavitating Flows”.Belgium: RTO，2001，Section8:1－27.

［9］SEMENENKO V N.Artificial supercavitation:Physics and calculation［C］//RTO AVT LectureSeries on“Supercavitating Flows”.Brussels，Belgium:RTO，2001，Section11:1－33.

［10］SAVCHENKO Y N.Experimental investigation of supercavitating motion of bodies［C］//RTO AVT Lecture Series on“Supercavitating Flows”.Brussels，Belgium: RTO，2001，Section 4:1－24.

［11］李裕春，时党勇，赵远.ANSYS11.0/LS－DYNA基础理论与工程实践［M］.北京:中国水利水电出版社，2008.