聚类算法在高脂血症辨证分型研究中的应用*

涂泳秋 易法令 朴胜华 周苏娟

（1.广东药学院医药信息工程学院 2.国家中医药管理局高脂血症调肝降脂重点研究室3.国家中医药管理局脂代谢三级实验室）

1 概述

高脂血症是血管及脏器疾病的主要基础病变之一，随着人们生活水平的提高，高脂血症的发病率呈逐年上升的趋势。中医药在防治高脂血症方面因其毒副作用小、疗效明显的优势而日益受到医学界的广泛重视。但是，由于传统中医没有高脂血症的病名，且病证分散，临床病变复杂，导致目前对高脂血症的辨病和辨证分型尚未有统一的标准[1]，不利于高脂血症中医辨证的规范化及对有效治疗方案的归纳总结，影响科研成果的客观评估和临床推广应用[2]。中医对于建立一个完善的规范化、客观化的高脂血症辨证体系的研究已持续了三十年[3]仍没有完全达到目标，探究其原因主要有以下两条：其一，中医对高脂血症的辨证分型主要根据古籍文献理论、患者主观表现及临床经验来确认，用来统计分析的样本存在片面性；其二，辨证体系、分型层次、学术流派及对兼夹证型认识的不同导致证型分类不统一，影响辨证分型的规范化[4]。

利用计算机挖掘技术建立疾病的中医辨证模型的研究正日益受到关注和重视[5～7]，高脂血症辨证分型的规范化研究一个重要难点在于证型分类不统一，利用聚类分析算法对临床四诊信息进行自动分类，获得统计学意义上的分类结果，并依此与已有证候表征进行比对，经过确定证型类别，发现了高脂血症四诊信息与辨证分型间的统计学规律，为高脂血症辨证分型标准化研究奠定基础，同时具有重要研究价值。

2 调查指标的设置

分析样本为临床采集的316例高脂血症患者中医四诊调查数据。通过对其进行聚类分析，获得相应的证型特点，与传统的证型分类方法进行比较，以进一步佐证传统分类方法的科学性。临床样本中记录了316例患者的基本信息、血液查验信息、中医相关症状的临床资料，包括患者的望诊、问诊、脉诊信息等共54项。部分信息如图1所示。

3 聚类分析方法

聚类分析，是按研究对象在性质上的亲疏关系进行分类的一种多元统计方法，能够反映变量或样本间的内在组合关系。基本思想是，从一批样品的多个观测指标中，找出能度量样品之间或指标之间的相似程度的统计量，构造一个对称的相似性矩阵，在此基础上进一步找寻各样本之间或样本组合之间的相似程度，按相似程度的大小，把样本逐一归类。关系密切的归类聚集到小的分类单位，关系疏远的聚类到大的分类单位，直到所有样品或变量都聚集完毕，形成一个亲疏关系谱系图，用以更自然、更直观地显示分类对象的差异和联系[8～10]。

聚类分析使用相似统计量进行分类，相似统计量是依据观测数据所建立的分类指标。本文中用到的相似统计量为距离系数、夹角余弦以及相关系数，其计算公式如(1)～(3)所示。

3.1 相似统计量

3.1.1 距离系数

假设有n个样本，每个样本有m个分量。这时每个样本可以看成是m维变量空间中的一个点，每个变量可以看成是n维样本空间中的一个点。用点的欧几里德距离表示研究对象的亲疏关系。距离越小，关系越密切；距离越大，关系越不密切。

用行表示样本、列表示变量的观测数据矩阵，样本间的距离系数如式(1)所示：

式中i,j = 1,2,...n，其中i，j均表示样本的序号，k表示样本中的分量号。

上面所定义的距离系数与变量的量纲有关，比如以米为单位时某变量为1，以厘米为单位时，就变成100，这会影响到距离的计算结果。为克服这个问题，在计算前需要对数据进行预处理。

此外，上面的距离系数要求与变量之间没有相关性。如果变量之间存在相关性，则会影响分类结果。有多个相关变量支持的分类特征比没有多个相关变量支持的特征，意味着有更大的权，在分类时会受到额外的“照顾”，因而有失公平。因此在算法实现中将使用逐步回归法剔除相关变量。

3.1.2 夹角余弦

夹角余弦用角度的分割表示样本之间的相似程度。在对样本进行分类时，可以把每个样本看成m维变量空间中的一个向量，样本Xi= (xi1,xi2,...,xim)与样本 Xj= (xj1,xj2,...,xjm) 之间的相似程度就可以用这两个向量之间的夹角余弦cosθ表示，cosθ的值在1和－1之间变化，如果等于1则表示两个样本非常相似，接近1则很相似，如果数值很小，则表示样本差异极大。夹角余弦的表达式如式(2)所示：

其中，i,j = 1,2,...,n。

3.1.3 相关系数

样本之间的相关系数如式(3)所示：

式中i,j = 1,2,...,n，i和j是样本号，n 是样本个数，m是变量个数。xia和xja分别表示i样本和j样本的平均值。

3.2 聚类分析的数据预处理

聚类分析的结果与量纲有关，为了消除量纲的影响，算法中用到了标准差标准化的数据预处理方法。计算公式如公式(4)～(6)所示。

标准差标准化预处理是将各个观测值减去观测值的平均值，再除以观测值的标准差，即:

xia是平均值，其表达式为：

si是标准差如式(7)所示，经过标准差标准化处理的所有观测值的平均值为0，标准差等于1。

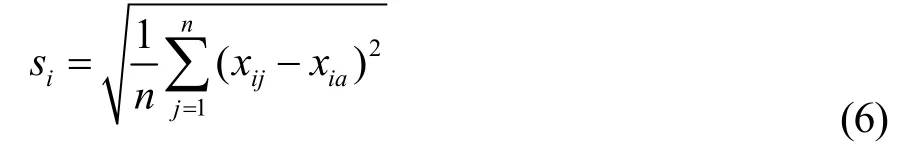
3.3 聚类算法构造

3.3.1 聚类算法思想

在聚类分析过程中，需要经过将类由多变少的聚类过程。其具体思想是：

（1）开始

每个样本自成一群；

（2）合并

① 计算类的分类统计量（距离系数、夹角余弦、相关系数）；

② 按某种分类统计量，将分类统计量最接近的两个样本（或群）合并成一群；

（3）求群的变量值

利用加权平均的方法求新群的各变量值。假定Li群与Lj群合并，Li群有Ni个样本，Lj群有Nj个样本，这时新群的k变量为：

（4）终止

重复（2）到（3），直到所有的类归为一群。

3.3.2 聚类算法

设定相似性条件P：0＜=P＜=1

（1）开始

所有样本归入同一群；

（2）计算：假如已分解为n个群C1,C2,………, Cn

① 计算类的分类统计量（距离系数、夹角余弦、相关系数）：假如 Cm中有 k个样本，则：Sm=sigma(cos(thetai,j))/k(k-1)

② 计算类平均相似性：S = (S1 + ……+Sn)/n

（3）判别

如果S＞=P跳到（5）终止。否则下一步。

（4）分解

对Sm＜P的每个类Cm, 对其中的每个样本I：

① 为I创建一个新类Cn+1，或将I归入其它类C1,…Cm-1,Cm+1,…,Cn中。分别计算S，使S增加最多的类获胜。

② 若Sm＞P，返回（3）

（5）终止

4 实验结果与评价

利用该程序对前期搜集到的316例高脂血症患者临床症状资料进行聚类分析，设置相似度阈值为75%，如图2所示。

图2 设置阈值界面

对预处理过的数据进行聚类分析，如图3所示，其中f1，f2……，f54分别对应中医症状特征信息如：体胖身重，心悸……，脉细等。程序得到的最终聚类结果如图4所示，将总样本自动分为5类，得到每类的相似性得分以及每类对应的实例个数。同时得到了每个分类中最具代表性和最不具代表性的样本实例所具有的特征，如图5所示。以第一类为例，最具代表性的样本具有体胖身重，头晕，失眠……等特征；而最不具代表性的样本具有体胖身重，头晕，面色淡白等特征。

图3 316例患者54种临床症状记录表截图

图4 316个样本的聚类分析结果

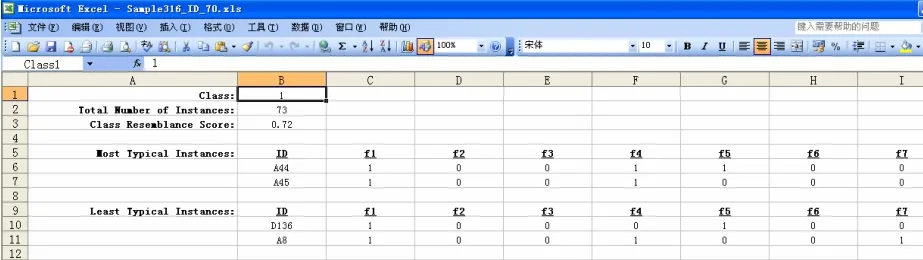
图5 第一种分类中最典型与最不典型症状表

将聚类算法得到的五类实例与中医师的证候判断结果对比发现，这五类实例中80%以上的样本分别对应于“痰湿内阻型”、“肝郁气滞型”、“气滞血瘀型”、“肝阳痰火型”、“脾肾阳虚型”五类证型，其中“肝阳痰火型”为兼杂证型。

5 小结

实现聚类分析算法并将其用于高脂血症临床病症中医证候研究中，通过对采集的临床四诊信息的聚类得到证候分型结果，与传统经验获得的证候分类相对照，得到基于统计分析的客观分类结果，为高脂血症证候标准化研究奠定了基础。

虽然聚类获得的五个分型结果都得到了 70%左右的相似度，但第四类与第五类证型的实例数较前三类明显偏低，因此高脂血症临床采集数据仍有待进一步扩充，使聚类的结果更科学客观。除此之外，下一步工作的重点是将模糊规则理论引入到聚类算法中解决兼杂证型的分类问题，将兼杂证型与其相关证型关联起来，而不再是完全独立的一个分型。

[1]黄波夫.中医治疗高脂血症研究进展[J].广西中医学院学报,2008,11(4): 102-104.

[2]陈建民.癌症患者血液高黏度状态与活血化瘀治疗[J].中西医结合杂志, 1985,5:89-91.

[3]唐沙玲.高脂血症中医研究进展[J].Internal Medcine of China.2008,3(1):129-131.

[4]钱小奇,陈红,田晓虹等.高脂血症中医辨证分析不一致探因[J].深圳中西医结合杂志,2007,17(2):25-26.

[5]王阶,李海霞,孙占全等.基于复杂算法的中医证候研究[J].北京中医药大学学报, 2006, 29 (9) : 581 – 585.

[6]白云静,申洪波,孟庆刚等.基于人工神经网络的中医证候非线性建模研究[J].中国中医药信息杂志.2007, 14(7):3-6.

[7]聂莉芳,于大君,余仁欢等.308例IgA肾病中医证候分布多中心前瞻性研究[J].北京中医药大学学报,2005,28(4):66-68.

[8]XU Rui, Wunsch., D. Survey of Clustering Algorithms[J].IEEE Transaction on Neural Networks, 2005,16(3):645-678.

[9]WANG Shi-tong, JIANG Hai-feng, LU Hong-jun. A New Integrated Clustering Algorithm GFC and Switching Regressions[J]. International Journal of Pattern Recognition and Artificial Intelligence, 2002,16(4):433-446.

[10]JIANG Sheng-yi, LI Xia. A Hybrid Clustering Algorithm[C].Fuzzy Systems and Knowledge Discovery, 2009, 1:366.