钢框架结构直接基于位移的抗震性能设计
吕大刚,贾明明,李 佳,张素梅
(哈尔滨工业大学土木工程学院,150090哈尔滨,jiamingming@hit.edu.cn)
直接基于位移的抗震设计(Direct displacement-based seismic design,DDBSD)主要是以结构在某水平地震作用下的预期目标位移响应为依据来进行结构设计,并希望设计的结构在未来实际发生该水平地震作用时恰好实现上述目标位移[1].基于位移的抗震设计方法通常要采用能力谱法通过迭代计算确定结构的性能目标,并据此对结构进行设计;而直接基于位移的抗震设计方法是一种可以直接基于结构的弹性或弹塑性位移谱确定结构的设计参数,进而确定结构的设计荷载和设计构件截面.直接基于位移的抗震设计方法在确定结构的设计参数时无需迭代计算,更加简便易行,而且更侧重于目标位移的实现过程,即如何通过设计,使给定的目标位移在设计水准地震作用下能够得到实现.从这个意义上讲,直接基于位移的抗震设计方法更能有效地实现基于性能的抗震设计思想[2].直接基于位移的抗震设计方法主要采用弹性反应谱等价线性化思想[3]以及基于非线性反应谱的设计思想[4],且都是采用单自由度体系等效多自由度体系.国内外学者对建筑结构、被动耗能结构、桥梁结构等结构体系直接基于位移的抗震设计方法进行了研究,对性能目标的确定方法、结构等效线性化方法和反应谱的建立方法进行了系统研究[5-14].在以往的研究中,直接基于位移的抗震设计方法的设计步骤都较为繁琐,并且研究的对象主要局限于钢筋混凝土结构,本文将直接基于位移的抗震设计方法用于钢框架结构,并给出了更加简便可行的设计步骤,并对基于弹性反应谱和基于弹塑性反应谱的直接基于位移的抗震设计方法进行了比较.
1 位移反应谱的建立
1.1 高阻尼弹性位移反应谱的建立
弹塑性体系的地震响应可以由等价的线性体系代替近似值估算得出,用等价线性体系设计弹塑性体系的方法也已被应用在基于位移的设计方法中.考虑一个在初始荷载作用下力-变形成双线性关系的单自由度弹塑性体系,如图1所示.弹性阶段刚度为k,屈服段刚度为αk.屈服力和屈服位移分别由Vy和Dy表示.顶点最大位移用Dm表示.延性系数μ=Dm/Dy.对于图1的双线性体系,与等效切线刚度ksec有关的等效线性体系的自由振动周期为

其中Tn为体系在线弹性阶段(V<Vy)的振动周期.
定义等效黏滞阻尼的大多数方法是使等价弹性体系和弹塑性体系的能量损耗相等,基于该准则,Chopra提出等效黏滞阻尼可以表示为

其中ED为弹塑性体系的能量损耗,其滞回曲线如图2所示.ES=ksecD2m/2为由ksec表示的体系的应变能.将ED和ES代入式(2),得

等效弹性体系的黏滞阻尼的总和为

其中ζ为双线性体系的弹性阶段(D<Dy)的黏滞阻尼比(通常取0.05),k为阻尼修正系数[15].
将我国抗震设计规范给出的阻尼系数为5%的弹性设计反应谱转化为阻尼为^ζeq的高阻尼弹性反应谱,将谱加速度-自振周期(A-Tn格式)曲线转化为位移-自振周期(D-Tn格式)表示的位移反应谱为


图1 双线性力-位移关系

图2 弹塑性单自由度体系的滞回曲线
1.2 弹塑性位移反应谱的建立
由于上述方法采用的反应谱是以不同等效阻尼比给出的等效弹性反应谱,这种方法用等效阻尼弹性反应谱代替阻尼比为5%的弹性反应谱,主要是依据等效过程和原过程的滞回耗能相等,但是滞回耗能和等效阻尼之间并不存在一个稳定的关系,因此导致的这个等效过程存在着很大的误差,有时甚至会导致对于层数大的结构计算不收敛,不便于实际工程应用.近年来,Chopra等[14]对以上不足进行了研究并提出了改进,其方法就是采用弹塑性反应谱的方法.采用与延性系数相关的弹塑性反应谱,在线弹性反应谱的基础上,通过对不同特性地震波的线性和非线性谱的计算与回归分析,得到了相应的与延性有关的非线性反应谱和线弹性反应谱的关系(用强度折减系数表示),具体表达式可参照相关文献.
强度折减系数为结构所承受的非弹性力与所承受的弹性力的比值:

由力的折减系数的物理意义可得

为区别弹性和弹塑性体系用Ae和De表示弹性体系反应谱的加速度和位移值.利用与延性系数相关的强度折减系数即可由线弹性反应谱来确定弹塑性反应谱,弹塑性谱对应的周期是结构弹性状态时对应的周期,理论上非弹性谱会比等效阻尼弹性谱更加精确,具有良好的物理基础,特别是在短周期范围内和高延性情况下更是如此.
同样将我国抗震设计规范给出的阻尼系数为5%的弹性设计反应谱利用强度折减系数转化为延性系数为μ的弹塑性反应谱,并依据式(5)转化为弹塑性位移反应谱.
2 直接基于位移的抗震设计步骤
2.1 高阻尼弹性位移反应谱的应用
利用高阻尼弹性位移反应谱进行直接基于位移的抗震设计可依据以下步骤:1)将结构体系转化为等效单自由度体系,结构的性能为双线性模型,并确定屈服位移Dy;2)确定结构的设计目标位移Dp,在本文中,结构的设计目标位移转角参考我国建筑抗震设计规范给出的钢结构“大震”作用时层间位移角限值θ=1/50确定;3)计算延性系数,已知的延性系数估计总的等效黏滞阻尼^ζeq,这里ζ是双线性体系的弹性阶段(V<Vy)的黏滞阻尼比(通常取0.05),k为修正系数;5)依据上节的方法建立高阻尼弹性位移反应谱;6)依据结构体系的设计目标位移Dp,在高阻尼弹性位移反应谱上确定对应的等效单自由度线性体系的自由振动周期Teq;确定等效切线刚度,其中m为结系确定必要的基底剪力Vy估计构件尺寸和细节设计;10)重复1~9步直到相邻两次所设计的结构的屈服位移与设计目标位移差值较小.
2.2 弹塑性位移反应谱的应用
利用弹塑性位移反应谱进行直接基于位移的抗震设计可依据下列步骤:1)~3)与应用弹性反应谱进行直接基于位移的抗震设计步骤的1~3步相同;4)依据上节的方法建立弹塑性位移反应谱;5)依据结构体系的屈服位移Dy,在弹塑性位移反应谱上确定等效单自由度线性体系的自由振动周期由式确定结构体系最初构体系的等效质量;8)由图1双线性力-位移关的弹性刚度;7)由式Vy=kDy确定必要的屈服力;8)由Vy估计构件尺寸和细节设计;9)重复1~8步直到相邻两次所设计的结构的屈服位移与设计目标位移差值较小.
3 算例分析
设计计算一个制糖车间多层钢框架,其横向为框架,纵向为支撑抗侧力体系,其中一框架形式如图3所示.梁柱节点刚接,采用现场焊接连接,屋(楼)面构造均采用预制肋式钢筋混凝土板上加40 mm配筋整浇层,外墙采用加气混凝土外包(200 mm)砌筑,并分别由各层强梁支托.
风荷载及雪荷载标准值分别为及0.4 kN/m2各层楼盖上活荷载标准值均为5.0 kN/m2,屋面活荷载标准值为7.0 kN/m2.抗震设防烈度为9度,场地类别为Ⅱ类,设计地震分组为第一组.框架梁、柱采用焊接工字型钢截面,梁、柱的截面尺寸列入表1中,材质均为Q235钢;弹性模量E= 2e8kN/m2,泊松比ν=0.3.
3.1 高阻尼弹性位移反应谱的应用
对此钢框架结构应用高阻尼弹性位移反应谱进行直接基于位移的设计.首先根据设计步骤假设屈服位移Dy为60 mm,设计目标位移Dp为300 mm,延性系数μ为5;经计算^ζeq=ζ+ζeq=;画出 ζ^=eq0.453 4的位移反应谱,如图4所示;由图4和 Dp=300 mm得Teq=2.06 1 s;切线刚度 ksec== 1 681.565 kN/m;屈 服 力 Vy==420.40 kN;将上述等价单自由度体系基底剪力按式施加到每一层上,则各层地震作用80.89 kN,F3=104.52 kN,F4=125.78 kN,F5= 61.80 kN;由上面所得数值,按照JGJ 99—98,柱和梁分别选用56a和40a工字型钢,对所设计结构进行非线性分析得Dy为75.53 mm,设计目标位移Dp为137.87 mm.所得结果与假设相差很大,重复上面步骤.

图3 5层两跨钢框架结构形式及其荷载分布

表1 梁柱截面尺寸 mm

图4 用弹性设计谱建立的的位移反应谱
最后边柱、中柱和梁分别选用截面为800× 400×12×16,900×450×14×18,700×300× 12×16的焊接工字钢(单位均为mm),对所设计结构进行非线性分析得Dy为50.01 mm,设计目标位移Dp为76.42 mm,所得结果与上一步结果相差不大,可以终止迭代.将上述迭代程序在表2中列出.
3.2 弹塑性位移反应谱的应用
对此钢框架结构应用弹塑性位移反应谱进行直接基于位移的设计.首先假设屈服位移Dy为60 mm,设计目标位移Dp为300 mm,则延性系数μ为5;由规范给出的加速度反应谱得到弹塑性反应谱,并得到相应的位移反应谱,如图5所示;依据Dy在图5位移反应谱上得出相应的周期Tn= 1.534;计算弹性刚度3 035.421 kN/m;屈服力Vy=kDy=182.13 kN;将上步得到的等价单自由度体系的基底剪力按式施加到每一层上,则各层地震作用F1=20.56 kN,F2=35.05 kN,F3=45.28 kN, F4=54.50 kN,F5=26.78 kN;由上面所得数值,梁、边柱和中柱分别选用32a,36a和40a工字钢,对所设计结构进行非线性分析得Dy为80.09 mm,设计目标位移Dp为159.57 mm.所得结果与假设相差太多,重复上面步骤.

表2 5层两跨钢框架结构应用弹性设计谱的迭代过程
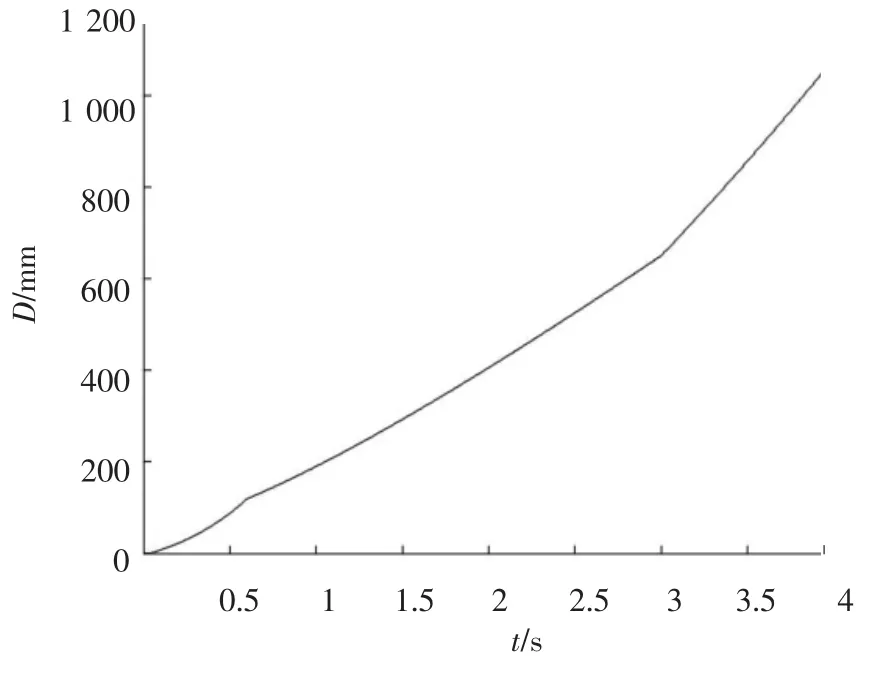
图5 应用弹塑性设计谱建立的μ=5的位移反应谱
最后边柱、中柱和梁分别选用截面为850× 400×12×16,1000×450×14×18,700×350×12× 16的焊接工字钢(单位均为mm),对所设计结构进行非线性分析得Dy为48.91 mm,设计目标位移Dp为82.75 mm.所得结果与上一步结果接近,可以终止迭代,上述的迭代步骤列于表3.
上面分别应用弹性反应谱和弹塑性反应谱对钢框架结构进行了直接基于位移的抗震设计.应用等效黏滞阻尼构造弹性反应谱精度较差,而弹塑性反应谱精度较好.从上面的设计结果也可以看出,两种方法得出的结果有所不同.在屈服位移基本相同的情况下,应用弹塑性反应谱比应用弹性反应谱设计的结构构件截面更大,设计偏于安全,因此应用有严格理论基础的弹塑性反应谱能更准确地对结构进行抗震设计.

表3 5层两跨钢框架结构应用弹塑性谱的迭代过程
4 结论
1)针对钢框架结构,基于大震时的结构位移限值,采用直接基于位移的抗震设计方法对结构进行设计,所设计的结构能够满足性能目标的要求.同基于位移的抗震设计方法不同的是,直接基于位移的抗震设计方法更侧重于目标位移的实现过程,即如何通过设计,使给定的目标位移在设计水准地震作用下能够得到实现.从这个意义上讲,直接基于位移的抗震设计方法更能有效地实现基于性能的抗震设计思想.
2)设计过程中采用单自由度体系等效多自由度体系,并采用弹性反应谱等价线性化思想以及基于非线性反应谱的设计思想构造了结构设计的位移谱.
3)弹塑性反应谱相对于应用等效黏滞阻尼构造的弹性反应谱精度更好,本文的研究也表明基于前者的直接基于位移的抗震设计方法的设计结果更加准确.
[1]吴波,熊焱.一种直接基于位移的结构抗震设计方法[J].地震工程与工程振动,2005,25(2):62-67.
[2]郭磊,李建中,范立础.直接基于位移的结构抗震设计理论研究进展[J].世界地震工程,2005,21(4): 157-164.
[3]PRIESTLEY M J,KOWALSKY M J.Direct displacement-based seismic design of concrete buildings[J]. Bulletin of the New Zealand National Society for Earthquake Engineering,2000,33(4):421-444.
[4]CHOPRA A K,GOEL R K.Direct displacement-based design:use of inelastic design spectra versus elastic design spectra[J].Earthquake Spectra,2001,17(1): 47-65.
[5]COURT A B,KOWALSKY M J.Performance-based engineering of buildings:a displacement design approach[R].Maui,Hawaii:SEAOC,1996.
[6]WALLACE J W.Seismic design of RC structural walls: new code format;applications[J].Journal of Structural Engineering,ASCE,1995,121(1):75-100.
[7]WIGHT G D,KOWALSKY M J,INGHAM J M.Direct displacement-based seismic design of unbonded posttensioned masonry walls[J].ACI Structural Journal,2007,104(5):560-569.
[8]PRIESTLEY M J.Direct displacement-based design of precast/prestressed concrete buildings[J].ACI Journal,2002,47(6):66-79.
[9]PRIESTLEY M J,KOWALSKY M J.Direct displacement-based seismic design of concrete buildings[J]. Bulletin of the New Zealand National Society for Earthquake Engineering,2000,33(4):421-444.
[10]LIN Yuyuan,CHANG Kuochun,CHEN Changyu.Direct displacement-based design for seismic retrofit of existing buildings using nonlinear viscous dampers[J].Bull Earthquake Engineering,2008,6:535-552.
[11]LIN Y Y,TSAI M H,HWANG J S,et al.Direct displacement-based design for building with passive energy dissipation systems[J].Engineering Structures,2003,25(1):25-37.
[12]JARA M,CASASB J R.A direct displacement-based method for the seismic design of bridges on bi-linear isolation devices[J].Engineering Structures,2006,28 (6):869-879.
[13]吴波,李艺华.直接基于位移可靠度的抗震设计方法中目标位移代表值的确定[J].地震工程与工程振动,2002,22(6):44-51.
[14]CHOPRA A K,GOEL R K.Direct displacement-based design:use of inelastic design spectra versus elastic design spectra[J].Earthquake Spectra,2001,17(1): 47-65.
[15]CHOPRA A K,GOEL R K.Capacity-demand-diagram methods for estimating seismic deformation of inelastic structures:SDF systems[C].The National Science Foundation of America:US-Japan Cooperative Research in Urban Earthquake Disaster Mitigation,1999:1-65.

