采用闭环双口RAM实现深空动态模拟源的设计

雷 鸣,李 珂

(中国西南电子技术研究所,成都 610036)

1 引 言

深空探测又称宇宙航行,包括空间探测器在太阳系内的行星际空间航行(航天)和太阳系外的恒星际空间航行(航宇)。当前,全球掀起了一场对宇宙深空进行探测的热潮。美国、俄罗斯、日本以及欧洲等国家和地区都在积极地开展深空探测任务。2008年,我国自主研制并成功发射的首颗绕月探测卫星——“嫦娥”1号月球卫星绘制了目前世界上最为完整的全月球影像图,可见我国在深空探测方面也取得了长足的进步。

测控信号的动态模拟是测控工作者长期以来追求的一个目标,期待用它来作为设备研制时的模拟源和系统联试或鉴定时的手段[1]。其中,深空动态模拟源的功能是接收地面基带调制器发出的调制信号,根据预设的卫星轨迹,对调制信号进行距离和速度的模拟,转发给基带接收机,使基带接收机解调出来的速度信息和距离信息能够符合预设的卫星轨迹。

2 工作原理

地面测控的测距原理都是测量发方发出的带有特殊标记的信号和航天器收到的测距信号再转发回地球站两信号之间的时间差[2]。测距的问题实质上就是测量电磁波信号在空中传播的时延问题,对距离的模拟也成了对时延的模拟。

在1988年10月世界无线电行政大会(WARC)ORB-88-610(为1988年大会发表的文件号码)把深空和非深空的界限规定在距地球地面2×106km处,这相当于太阳和地球对航天器引力的平衡点[3]。根据这个距离计算出深空电磁波传播的最小双向时延τ如下:

式中,R为卫星到地面站的单向距离,C为光速(299792458 m/s)。

当航天器相对于地面站高速运动时,地面站接收到的航天器发射的信号中包含有多普勒频移。现代地面测控的测速方法是测量航天器与地面站相对运动的径向速度所引起的载波上的多普勒频移,也可直接称其为多普勒频率或多普勒,再由多普勒频移推算出径向速度。常用的多普勒频移测量的方法可分为单程多普勒频移测速、双程多普勒频移测速和GPS(全球定位系统)测速[4]3种,由于GPS系统的卫星轨道高度为20200 km,与深空定义的2×106km相差甚远,故不在本文讨论的范围内。

在单程多普勒频移测速的情况下,卫星的径向速度与多普勒频率之间的关系如公式(2)所示:

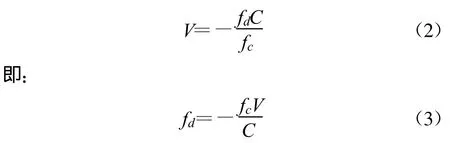
式中,fd为多普勒频率,fc为载波频率,C为光速,V为卫星径向速度。

在双向多普勒频移测速的情况下,卫星的径向速度与多普勒频率之间的关系如下:

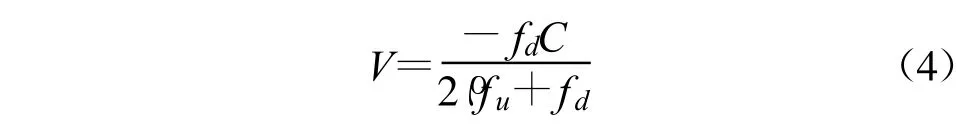
即:

式中,fd为多普勒频率,为转发比,fT为下行频dT率,fu为上行频率,C为光速,V为卫星径向速度。

图1是在地球表面上不动的地面测控站接收到的探测卫星信号中的多普勒频率Δf与时间t的关系。当卫星向目标飞近时所接收到的频率增大,而离去时频率下降。曲线的符号变化点表示多普勒频率为0,在卫星最接近于测控站的位置发生。在这一点上,卫星相对于地面站速度的径向分量为零,当卫星经过这一点时,多普勒的符号将发生改变。

3 距离模拟的实现

由公式(1)的计算可知,深空中探测卫星信号的双向传播时延至少约为13.34 s,作为深空动态模拟源就需要至少能够模拟13.34s的时延。由于13.34s的时延较长,不可能利用延迟线、锁存器等比较简单的方式实现。在实际工程中,可以采用闭环双口RAM来进行时间的延迟。

连续波测控信号的测距是用测相来实现的,目标运动时距离的变化就直接表现为接收到的信号的相位发生变化。闭环的双口RAM循环地存储地面测控站送入的信号相位值。当仿真开始时,系统就以固定的写入频率从首地址开始往双口RAM实时写入相位值。根据写入数据的频率以及需要仿真的初始距离计算出延迟的存储单元个数,然后以该单元的地址为初始地址开始读出相位数据。其中读地址和写地址之间相差的N个存储单元就相当于模拟的信号被延迟了N个存储单元的时延。当读出数据的地址大于RAM的最高地址时,读出数据的地址自动归零,地址重新开始累加,如此循环下去。

在考虑信号传播的双向时延的情况下,仿真距离与延迟的存储单元之间的关系如下:

式中,R为仿真的距离,N为延迟的存储单元的地址,fw为写入数据的频率,C为光速。

能够模拟的最大距离取决于RAM的最大容量以及向RAM写入数据的频率,具体关系如下:

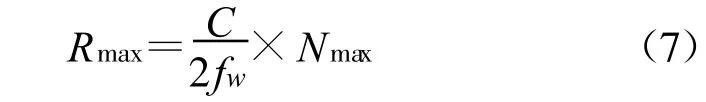
式中,Rmax为能够仿真的最大距离,Nmax为RAM的存储容量的最大值,fw为写入数据的频率,C为光速。

模拟距离的精度取决于RAM的最小时延Δτ,也就是一个存储单元能够产生的时延。一个存储单元的时延与写入RAM的时钟频率的关系如下:

由上述公式可以看出,在模拟的最大距离一定的情况下,写入的时钟频率越高,一个存储单元产生的时延就越小,相应的模拟的距离精度也就越高,但是所需要的RAM存储容量会相应增大。在工程应用中,设计者应结合实际情况,根据系统提出的精度指标要求,合理选择写时钟频率和相应的RAM存储容量。

4 速度模拟的实现

在工程中,模拟探测卫星的运动速度其实也就是对探测卫星发出的电磁波信号频率进行相应的拉偏,产生多普勒频率。本文将向RAM写入数据的速率记为fw,从RAM中读出数据的速率记为fr,改变读出数据的频率fr就可以产生多普勒频偏。

当 fr>fw时,通过图2和图3可以看出,经过 fr恢复出来的信号频率变大,这就相当于在原信号频率的基础上添加了一个正的多普勒偏移;当 fr

图2 向RAM写入的信号Fig.2 The signal written to RAM

图3 从RAM读出的信号Fig.3 The signal read from RAM

写入频率fw、读出频率fr与多普勒频率fd的关系如下:

式中,fs为地面站的主测音频率。由于写入RAM的频率fw是固定的,根据上述公式在已知卫星多普勒频率fd的情况下,可以计算出从RAM中读出数据的频率fr:

在实际工程中,卫星与地面站之间的距离总是大于零的,电磁波信号的传输时延也一定是大于零的,所以读出数据的地址总是小于正在写入数据的地址。在仿真模拟的时候,尽管fr>fw,但绝对不会出现读数据的地址跃过写数据的地址,或者读数据的地址等于写数据的地址的情况。

5 信号电平的模拟

在不考虑电波传播空间中的折射、反射、散射和吸收等能量损耗的理想情况下,可以认为电波是在自由空间传播的,其能量的扩散损耗(Lr)与电波传播距离R的平方成正比,与电波波长λ的平方成反比。由于距离传输导致的信号电平的模拟可以根据公式(11)计算:

在工程中是通过控制数控高精度衰减器来实现信号电平的模拟。由于从深空中传送过来的电磁波信号微弱,所以对衰减器的精度指标要求较高。

6 影响距离和速度模拟精度的原因分析

动态模拟源的误差主要来自时钟、卫星轨迹曲线数据文件和DDS引入的误差。

6.1 fr时钟引入的误差

由上文的描述可知fr时钟必须是实时可变,在实际设计中就不能简单地利用分频电路来产生,本文利用DDS来生成 fr时钟,而系统又是依靠A/D对基带调制器发出的调制信号进行采样,A/D是直接分频产生的。DDS产生的 fr与A/D采样的信号之间的相位会产生随机的晃动,这将直接影响模拟源模拟出来的距离和速度的精度。

6.2 卫星轨迹曲线数据文件的误差

模拟源以20 Hz的固定频率从实际的记录卫星轨迹曲线的数据文件中读取卫星的径向速度进行仿真,在两次读取卫星速度的时间空隙中,就认为卫星是匀速运动的,但实际情况是在这段时间中卫星往往不是匀速运动的,这样仿真出来的卫星距离与实际的距离就会有误差,且随着仿真时间的推移,距离误差累积。在硬件和指标要求满足的情况下,适当提高模拟器读取卫星轨道数据的频率能够降低模拟的距离误差。

图4 距离误差累积示意图Fig.4 Illustration of the accumulated distance error

6.3 DDS引入的误差

实际工程中是由DDS产生的读RAM时钟。模拟源根据记录卫星轨迹曲线的数据文件,以20 Hz的频率改变RAM的读时钟。每改变一次DDS时钟频率,DDS产生的相位就会跳变,这种跳变将直接引起模拟的径向速度产生突跳以及距离的变化率发生偏差。其中距离变化率的偏差能够引起模拟距离的误差,且随着时间的推移,距离误差逐渐累积。

7 结束语

由于深空动态模拟源具有时延巨大、信号幅度较小等特点,使得深空动态模拟源相对于普通模拟源来说,设计的难度较大。本文就解决模拟时延太长和模拟的探测卫星的径向速度较大的难点提出了利用闭环双口RAM产生时延的方案,该方案已经用于实际的工程中。实践证明本方案结构简单,实现容易,实现成本较低且完全可以满足深空探测的需要,在工程中可以广泛采用。但是当模拟的距离为极远距离时,比如探测火星,距离达到4.013×108km时[5],时延达到约3000 s,利用该方案模拟时延实现起来就比较困难了,有待进一步的深入研究。

[1]刘嘉兴.基于运动方程的动态模拟方法[J].电讯技术,2010,50(11):1-4.LIU Jia-xing.Dynamic SimulationMethod Based onMotion E-quation[J].Telecommunication Engineering,2010,50(11):1-4.(in Chinese)

[2]邓永铭.采用开环模式实现深空动态模拟源设计[J].电讯技术,2009,49(7):73-76.DENG Yong-ming.Implementation of Dynamic Simulating Source Design by Using Open Loop Mode[J].Telecommunication Engineering,2009,49(7):73-76.(in Chinese)

[3]姜昌,范晓玲.航天通讯跟踪技术导论[M].北京:北京工业大学出版社,2003.JIANG Chang,FAN Xiao-ling.The Aerospace Communicationand Tracking Introduction[M].Beijing:Beijing University of Technology Press,2003.(in Chinese)

[4]统一载波测控讲义[M].成都:电子工业部第十研究所,1997.The T eaching Materials of Unified Carrier TT&C[M].Chengdu:The 10th Institute of Electronic Industry,1997.(in Chinese)

[5]柴霖,许秀玲.深空测控体系结构与技术发展[J].电讯技术,2010,50(8):1-6.CHAI Lin,XU Xiu-ling.Archiecture and T echnology Development of Deep Space TT&C Communication System[J].Telecommunication Engineering,2010,50(8):1-6.(in Chinese)