高速铁路长大桥梁无缝线路附加挠曲力计算分析

孔文斌，雷晓燕

（华东交通大学铁路环境振动与噪声教育部工程研究中心，江西南昌 330013）

我国高速铁路长大桥梁以无砟轨道和跨区间无缝线路作为主要结构型式。跨区间无缝线路是轨条长度跨区间且轨条与道岔直接连接的无缝线路。它最大程度地减少了钢轨接头，实现了线路的无缝化，消除了缓冲区和伸缩区的影响[1]，由于钢轨不能自由伸缩，在列车荷载作用下，梁发生挠曲变形，梁的上翼缘受压缩短，下翼缘受拉伸长。梁轨产生相对位移并通过扣件给钢轨施加纵向水平力，称为附加挠曲力。目前，国内外学者对于桥上无缝线路钢轨附加挠曲力的研究大都是针对有砟轨道，采用数值解析的方法进行计算，对于桥上无砟轨道钢轨附加挠曲力的研究则比较少[2-8]。本文将结合京沪高速铁路长大桥梁无砟轨道无缝线路实际情况，建立京沪高铁整桥双线模型，利用ANSYS软件对高速铁路长大桥梁无砟轨道无缝线路附加挠曲力进行计算分析。

1 有限元模型

1.1 有限元模型的基本假设

1）计算附加挠曲力时，不考虑其它力对附加挠曲力的叠加。

2）假设梁的位移能被固定支座完全阻止，不考虑活动支座所产生的摩擦阻力，也不考虑支座的纵向刚度，计算伸缩量时按计算跨度计算。

3）线路纵向阻力的取值：本文为无砟轨道，故线路纵向阻力为扣件阻力。

4）计算附加挠曲力时，不考虑冲击荷载，列车荷载分段进入梁内，分段长度可以按一个单元长度取值。5）假设桥梁墩台纵向水平线刚度为线性，计算时不考虑固定支座纵向刚度的影响。

1.2 有限元模型的建立

如图1所示，本模型中的钢轨、梁和墩台采用beam 3梁单元来模拟，扣件纵向阻力采用combin 39非线性弹簧单元来模拟，墩台刚度采用combin 14线性弹簧单元来模拟。由于非线性弹簧单元无法传递结构竖向力，为了使挠曲力能通过轨道直接加载，故扣件垂向力学特性也采用combin 14线性弹簧单元来模拟。在钢轨的一定位置约束其侧向位移，两端不施加纵向约束，采用双支座，同时约束轨道结构的横向扭转。

整桥全长取10跨32 m，共320 m，单元长度取实际扣件间距0.65 m。桥梁两端路基上钢轨各延长100 m，从而消除了路基对纵向力的影响。整桥总共有单元数10 926个，其中双线四轨道钢轨单元总个数为3 200，简支箱梁单元数为496个，模拟扣件纵向阻力的非线性弹簧单元数为3 204个，模拟扣件垂向力学特性的线性弹簧单元数为3 204个，模拟墩台刚度的线性弹簧单元数为22个，横向刚臂单元数为800个。

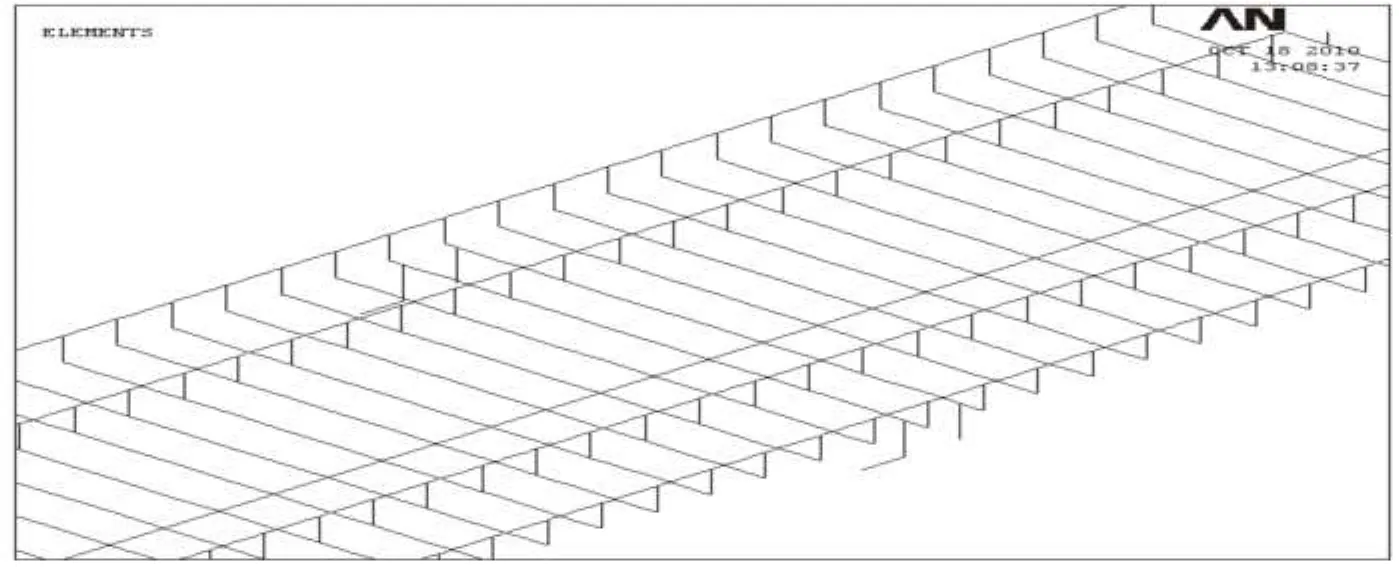
图1 京沪高铁整桥双线有限元模型Fig.1 Finite element model of the whole bridge with double bound railways for Jing-Hu high-speed railway

2 计算分析

本文所采用计算参数为钢轨取CHN60型钢轨，其弹性模量E=2.06×1011N·m-2，截面积F=7.745×10-3m2，热膨胀系数a=1.18×10-5/℃；梁选用京沪高铁采用的32 m箱梁，其弹性模量E=3.455 4×107N·m-2，截面积F=8.272 m2，热膨胀系数a=1×10-5/℃；墩台刚度依据《新建铁路桥上无缝线路设计暂行规定》和德国DS899/59《铁路新干线上桥梁的特殊规程》，相关取值为两边桥台刚度值皆为4 000 kN·cm-1，中间9个桥墩刚度值皆为1 000 kN·cm-1；扣件纵向阻力依据德国理想弹塑性模型和《新建时速300～350公里客运专线铁路设计暂行规定》，相关取值为桥梁两侧路基上无砟轨道纵向阻力采用图2所示阻力，桥上则采用如图3所示纵向阻力；对于列车荷载，依据《高速铁路设计暂行规定》，客运专线以及高速铁路采用ZK标准活载即0.8UIC标准活载，见图4。

以京沪高速铁路无砟轨道双线整孔10跨简支箱梁桥为例，运用所建立的京沪高铁整桥双线有限元模型对其进行附加挠曲力静力非线性分析。荷载布置图如图5所示。

如图5所示，桥梁跨度取为32 m，桥跨数为10跨，两侧路基各延伸100 m，钢轨为CHN60型钢轨。对钢轨纵向力及纵向位移进行图示时，坐标原点为0号桥台处，横坐标为钢轨离0号桥台的距离。

通过ANSYS计算得到有载侧钢轨附加挠曲力图、有载侧钢轨附加挠曲位移图、无载侧钢轨附加挠曲力图、无载侧钢轨附加挠曲位移图，分别见图6-9所示。

由图可知，列车在双线简支箱梁上单线运行时，其附加挠曲力值较小。钢轨附加挠曲力在桥台处较大。钢轨纵向位移则在桥梁中部较大，在桥台处较小。4根钢轨的附加挠曲力有所差别，但差别不大，主要原因是双线箱梁具有很强的整体性，尽管荷载偏心，每股轨线下桥梁垂向位移有较大的差别，但同一断面梁顶面各点的纵向位移近乎相等，而由梁顶面纵向位移引起的附加挠曲力也很接近。

3 结论

在高速铁路长大桥梁梁轨相互作用原理基础上，建立了京沪高速铁路整桥双线有限元模型，并选取了长大桥梁钢轨纵向力的计算参数，以京沪高铁10跨32 m混凝土简支箱梁为例，对高速铁路长大桥梁无砟轨道无缝线路附加挠曲力进行了计算分析，计算结果反映了高速铁路长大桥梁无砟轨道无缝线路附加挠曲力的基本规律。

[1]张未，张步云.铁路跨区间无缝线路[M].北京：中国铁道出版社，2000.

[2]DR IR，HADIETERMAN.Longitudinal forces in railroad structures[J].Rail Engineering International，1990，1（6）：46-53.

[3]FRYBAL.Thermal interaction of long welded rails with railway bridges[J].Rail International，1985，16（3）：5-24.

[4]杨少宏.桥上无缝线路挠曲附加力的研究[D].兰州：兰州铁道学院，1990.

[5]蒋金洲.桥上无缝线路钢轨附加纵向力及其对桥梁墩台的传递[J].中国铁道科学，1998，19（2）：67-75.

[6]卢耀荣，冯淑卿.桥上无缝线路挠曲力的计算[J].铁道学报，1987，9（2）：56-67.

[7]叶庆发，唐进锋，于雷，等.桥上无砟轨道无缝道岔挠曲力与位移特性分析[J].中国西部科技，2009，8（15）：7-10.

[8]朱传勇，唐进锋，叶松.特殊设计的简支梁桥无缝线路挠曲力计算分析[J].山西建筑，2007，33（19）：302-303.