基于滑移网格与RNG k-ε湍流模型的桨舵干扰性能研究
王 超,黄 胜,常 欣,郭春雨
(哈尔滨工程大学 船舶工程学院,哈尔滨 150001)
1 引 言
由于螺旋桨和舵都布置在船后,而且相互比较接近,因此存在着相互干扰,由于这种干扰,作用在螺旋桨上的水动力不仅与其本身的要素、船体要素有关,而且与其后方的舵也有密切的关系。同时,由于舵工作在螺旋桨的尾流中,作用在其上的水动力性能也与敞水舵的情形不同[1]。积极利用桨舵的有利干扰可以提高推进效率,从操纵性和耐波性的观点看,螺旋桨尾流对于利用舵控制航向和减摇都有较大的影响[2]。因此,桨舵的相互干扰研究有十分重要的意义。
由于流体机械中的螺旋桨与舵之间存在相对运动,使得它们之间在运动中存在动静干扰的问题,使其内部流动呈现为非定常的湍流特征。文中利用滑移网格技术在螺旋桨与固定舵之间引入交互界面,并利用三维Navier-Stockes方程结合RNG k-ε湍流模型,计算并分析了桨舵干扰的水动力性能问题。
2 控制方程与湍流模型
2.1 控制方程
螺旋桨是在流场中作旋转运动,在绝对静止坐标系下,由于螺旋桨与舵之间的相互干扰作用,在计算时整个流场应是非定常的。RANS方程是粘性流体运动学和动力学的普适性控制方程,所以本文以之为求解桨-舵干扰水动力性能计算的基本方程,其形式如下[3]:
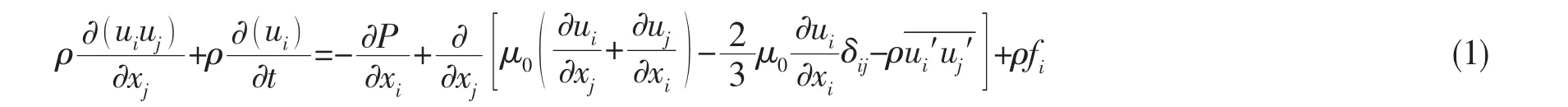
式中:ui,uj为速度分量时均值 (i, j=1,2,3),P为压力时均值;ρ为流体密度; μ0为流体粘性系数;fi为单位质量的质量力;-为雷诺应力项。
2.2 湍流模型的选取
就目前湍流研究进展来看,湍流的内在机理还没有真正被人们所了解,迄今尚未认定一种解决湍流问题的最佳方法,而且目前关于螺旋桨及舵粘性绕流场数值计算方面的可供参考文献较少[4-9]。与标准k-ε湍流模型相比,RNG k-ε湍流模型通过修正湍流粘度,考虑了平均流动中的旋转及旋流流动情况[3],因而可以较好地用来处理螺旋桨的旋转运动问题。
RNG k-ε湍流模型的基本方程如下:
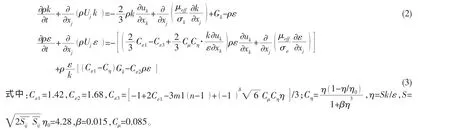
3 滑移网格技术
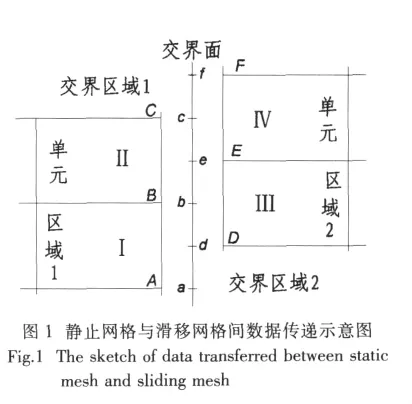
滑移网格模型可使在交界面两侧的网格相互滑动,而不要求交界面两侧的网格结点相互重合。但要计算交界面两侧的通量,并使其相等。为了计算交界面的通量,首先在每一新的时间步确定出交界面两边交界区的重合面。基本上,通过网格重合面的通量,是由交界面两边交界区的重合面计算,而不是用整个交界面计算。在非定常流动计算中,在流体机械的旋转部件出口与固定部件进口间形成网格滑移的交界面,如图1所示。当转子和定子的交互作用应用实时解法(而不是时均解法)时,必须用滑动网格模型计算非稳态流场。
4 计算的前处理
4.1 几何模型与计算域的创建
计算所选用的模型是B4-70型螺旋桨与NACA剖面系列舵[10]。其主要几何参数为:螺旋桨,B4-70,P/D=1.0,D=0.24 m;舵为NACA剖面,展长L=0.3 m,展弦比AR=1.35,厚度比t/c=0.18。
在建模过程中使用的是直角坐标系O-XYZ,坐标原点取在螺旋桨桨盘面的中心点上,X轴方向代表来流方向,它沿着螺旋桨的旋转轴指向下游,Y轴与螺旋桨的某一桨叶的叶面参考线一致,Z轴服从右手定则。由于研究的是在粘性流场中螺旋桨与舵相互干扰的水动力性能,因此需要把模型置于流场域中。由于用到滑移网格计算方法,需要把螺旋桨置于一个为桨直径1.1倍的小圆柱域中,此小域的内边界取在桨毂和叶片表面上,其中桨毂被简化为中间是圆柱面,两端为椭球面。为了计算的需要,把整个大域分成几部分,这样便于在划分网格时进行局部加密,提高计算结果的准确度。具体计算域的划分见图2。
4.2 网格的划分
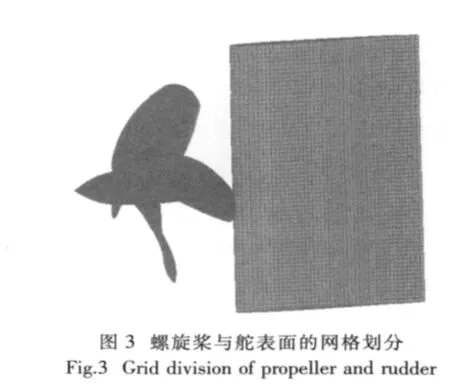
高质量的网格是实现数值模拟成功的首要条件,过疏或过密的网格都会极大影响计算结果。该文在计算过程中计算网格采用非结构化网格,非结构化网格方法是数值求解流动问题的很有效方法,它可以采用任意形状的单元作为有限控制体,具有良好的贴体性及自适应性。文中在划分网格时使用了局部加密的方法,对于桨叶与桨毂连接处以及叶梢部分等进行加密,以便捕捉到重要的流场信息;而对于出口段的网格,将其密度适当降低,便于控制总网格数。这样,在网格模型总节点数一定的情况下可以提高计算精度,还可以避免流场变化平缓区域的计算资源浪费。螺旋桨桨叶表面以及舵表面的网格划分如图3所示。

4.3 边界条件的设置
在进口边界处设置为速度进口条件,出口边界定义为压强出口;fluid1与fluid4之间相互结合的圆柱体表面设为interface面;壁面设为无滑移固壁条件,在近壁区采用标准壁面函数并考虑壁面粗糙度的影响。
5 计算结果对比分析
敞水螺旋桨和舵前螺旋桨的性能是不一样的,试验和理论计算都表明舵对螺旋桨的性能一般是产生有利干扰的。以往实验表明舵对螺旋桨性能的影响与螺旋桨的负荷系数、桨舵间距、舵角、舵的展弦比和厚度比等有关[2],下文就螺旋桨的负荷系数和桨舵间距X/D对桨舵干扰的水动力性能的影响进行了计算分析。
5.1 舵的存在对螺旋桨性能的影响
以进速系数J=0.6为例,螺旋桨转速为一定值,n=600 rpm,舵角为零,桨—舵间距X/D=0.5,分析由于舵的存在螺旋桨的性能随时间的变化规律。通过FLUENT模拟计算,从计算结果中提取出不同时刻的螺旋桨推力以及舵的阻力值,然后利用公式转换,获取螺旋桨的推力系数曲线和舵的阻力系数曲线,见图4和图5。
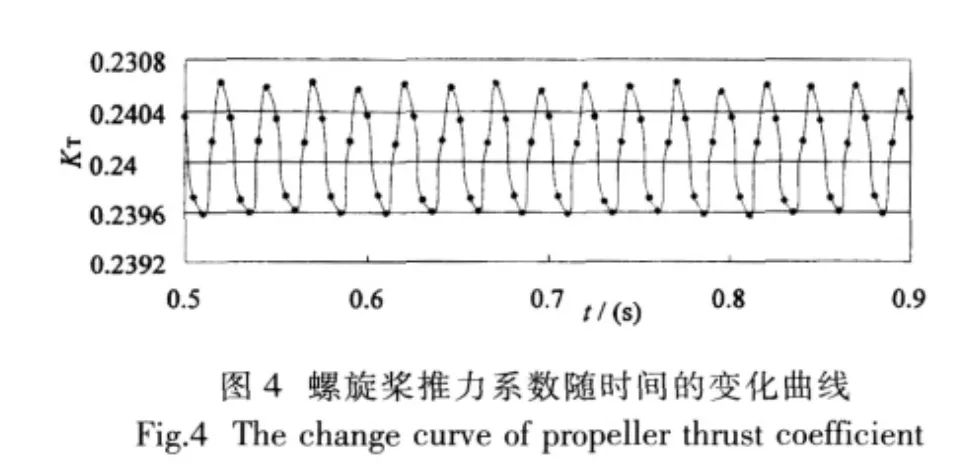
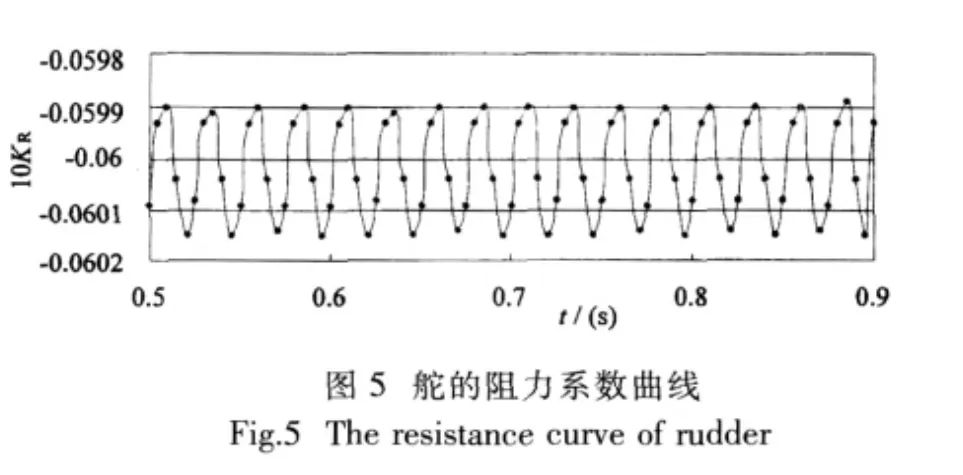
由图4看出由于舵的存在使螺旋桨敞水时固定的推力系数值变成周期性变化的值。螺旋桨旋转一周的时间为0.1s,螺旋桨为4叶桨,从图4和图5中可以看出螺旋桨旋转一周,螺旋桨的推力变化和舵的阻力变化都经过4个周期。由图4和图5可以获知两种系数的平均值分别约为0.24和-0.006 005,得出舵的阻力约占螺旋桨总推力的2.5%;同时可以查出螺旋桨的推力系数时均值比试验值[9]要有所增加。
5.2 进速变化对桨—舵干扰水动力性能的影响
进速系数J分别取为0.2,0.4,0.6,0.8,1.0,螺旋桨转速n=600 rpm,舵角为零,桨—舵间距X/D=0.5,进速系数的变化通过改变来流流速大小来实现。通过模拟计算,提取出不同进速系数J情况下的螺旋桨推力与转矩的时均值,进而求出螺旋桨的推力系数KT、转矩系数KQ。把通过公式转换求得的特性曲线结果与试验值[10]一起绘制成图,见图6和图7。
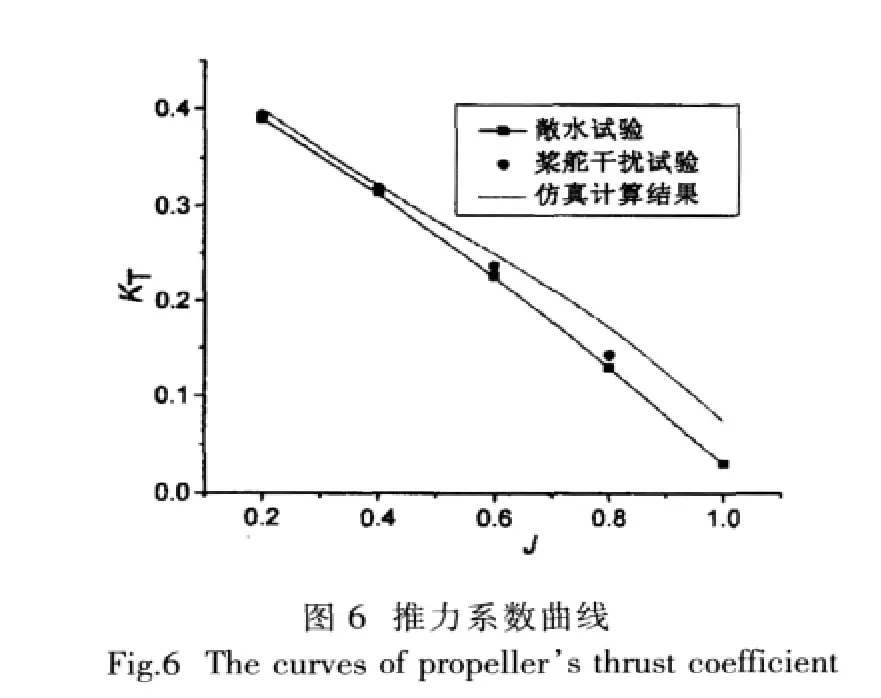
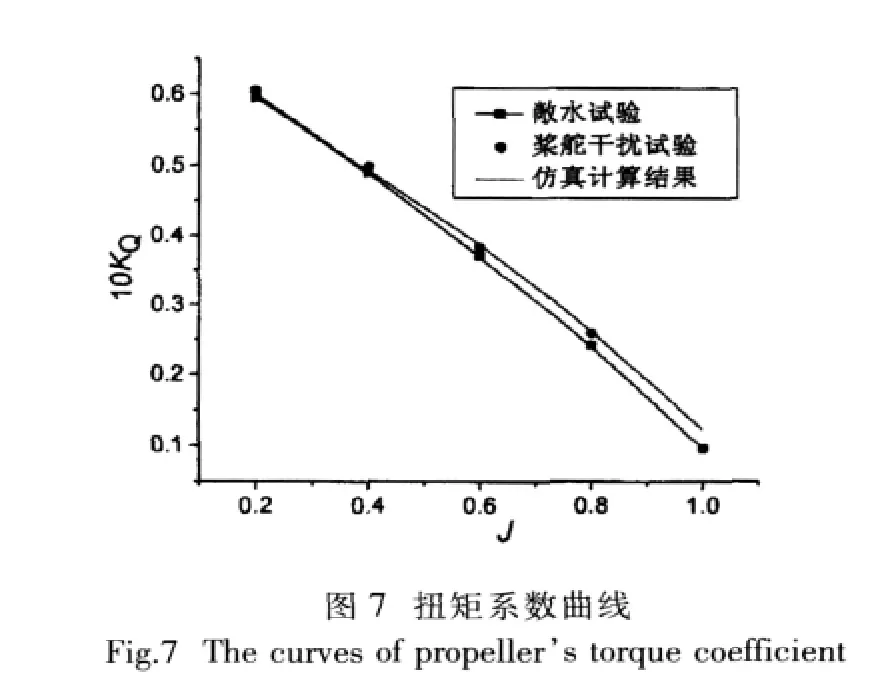
在图6和图7中可以看出:舵的存在会使螺旋桨的推力系数KT和转矩系数KQ均有相应的增加。而且可以得出:与敞水试验结果相比,螺旋桨的推力系数KT和转矩系数KQ的增加量ΔKT和ΔKQ随着进速系数J的增加也相应地增加(或者说随着螺旋桨负荷系数的增加而减少)。这可解释为当螺旋桨轻负荷时(进速系数较大时),桨后的流动状态接近绕流流动,此时舵起到整流作用,改善了螺旋桨的推进性能,而螺旋桨为重负荷时,桨后的流动状态接近于射流流动,舵对螺旋桨性能的影响必然会减弱[2]。
总的来说,在考察的进速系数范围内(0.2~1.0),采用RNG k-ε模型和滑移网格技术所计算的结果与试验结果相比,转矩系数KQ的计算结果与试验结果基本上一致,只是在斜率上稍有偏差;而推力系数KT在0.2≤J≤0.4的情况下两者基本重合,J超过0.4后差距逐渐变大。
5.3 桨—舵之间的距离的改变对桨—舵干扰性能的影响
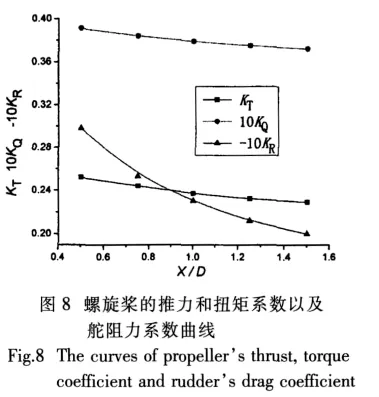
桨舵间距比X/D中的X为舵前缘到螺旋桨参考面的距离。为了分析桨舵间距的改变对螺旋桨的水动力性能的影响,该文计算时分别取X/D为0.5、0.75、1.0、1.25和1.5,进速系数取为J=0.6,螺旋桨转速n=600 rpm,舵角为零。
图8中给出了在不同的桨—舵间距状态下,螺旋桨的推力系数KT和转矩系数KQ和舵阻力系数的时均值。可以看出随着间距比的增加,推力系数KT和转矩系数KQ的增加量在减小,舵的阻力系数也在下降,从而表明随着桨—舵间距的增大,桨—舵相互干扰作用减小。
5.4 桨—舵表面压强分布
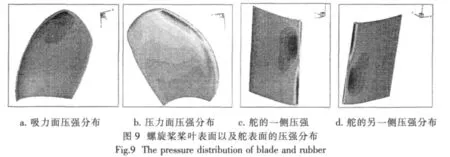
如果要细致地研究流体中螺旋桨的受力情况,需要对螺旋桨表面任意点的受力进行研究。现以螺旋桨在X/D=0.5和进速系数J=0.6时的工况为例,对桨叶以及舵表面的受力情况进行分析。图9给出了某一计算时刻螺旋桨以及舵表面上的压强分布。在螺旋桨压力面上,从叶根到叶梢,压强不断增加,在0.8r左右达到最大,然后逐渐减小,在叶梢处达到最小值;而且,明显可以看出压力由随边向导边逐渐增大,在导边处达到最大。在螺旋桨吸力面上,压强分布的主要特点是靠近叶梢的相当一部分压强较小,如考虑螺旋桨的空泡性能,则此部分最容易出现空泡。从舵面两侧的压强分布可以看出:舵两侧的表面受力呈现近似的反向对称分布,这主要是由于螺旋桨的螺旋尾涡流作用在舵表面两侧的攻角方向相反而产生的;同时可以看到在舵的导边部位受力最大,接着迅速减小,随后沿着去流方向又逐步地增加。
5.5 舵对螺旋桨尾流场的影响
由于舵的干扰作用,螺旋桨的尾流场受到较大的影响。为了更好地了解舵的存在对螺旋桨尾流场的影响,该文给出了相同来流情况下有舵和无舵时螺旋桨后某截面处的各向速度分布(x=0.1属于桨舵之间的一个截面,x=0.3为舵后的截面),见图10。

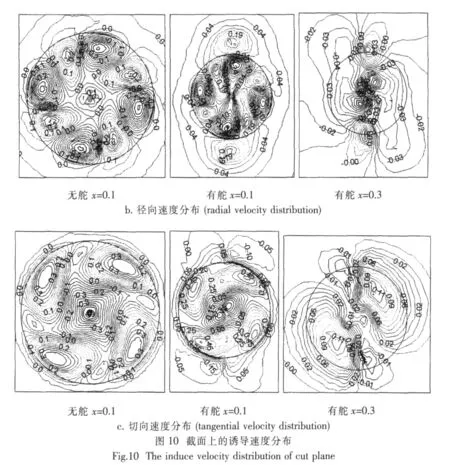
从图10可以看出:首先、由于舵的存在,径向与切向速度分布呈现向上下伸展的分布形状,而轴向速度恰恰相反。第二、舵前x=0.1截面上的各向速度分布虽然相对于无舵时有所变化,但可以看出两者的基本分布形式还是比较相似的,但舵后x=0.3截面上的各向速度分布与前两者有非常大的变化。第三、在x=0.3截面上可以明显看到径向与切向速度分布呈现舵的左舷侧下方和右舷侧上方(从舵的导边往随边看)为加速域;而轴向速度虽也有上述规律,但很不明显,不过可以看到相对于x=0.1截面轴向速度在截面中心部位速度增加不少,而在叶梢附近的轴向速度却相对减小。
6 结 论
本文采用计算流体力学软件计算了粘性流场中螺旋桨、舵组合体的水动力性能。通过上述的分析可以得出以下结论:
(1)通过不同的进数系数下螺旋桨的推力系数,转矩系数的计算值与实验值的对比分析,可以看出虽然二者尚还存在一定的差距,但基本上可以反映出桨—舵相互干扰的水动力性能。因而,CFD数值计算可以作为一种技术和手段应用于桨—舵干扰研究之中。
(2)舵的存在会使螺旋桨的推力系数和转矩系数均有相应的增加。与敞水试验结果相比,螺旋桨的推力系数和转矩系数的增加量ΔKT和ΔKQ随着螺旋桨负荷系数的增加而减少。
(3)随着桨—舵间距的增加,推力系数和转矩系数的增加量在减小,舵的阻力大小也在下降,从而表明随着桨—舵间距的增大,桨—舵相互干扰作用减小。
(4)对螺旋桨桨叶表面以及舵表面压力分布进行了考察与分析,得出:桨叶压力面上的压力由叶根至叶梢,压力不断增加,在0.8r左右达到最大,然后逐渐减小,在叶梢处达到最小值;而且,可以看出压力由随边向导边逐渐增大,在导边处达到最大。在吸力面,压力分布的主要特点是靠近叶梢的相当一部分压力较小,如考虑螺旋桨的空泡性能,则此部分最容易出现空泡。同时可以看到舵的两侧压力分布近似呈现反向对称关系。
(5)分析了舵的存在对螺旋桨尾流场分布的影响,通过观察与分析各截面处的速度分布云图得出:舵的存在,使径向与切向速度分布呈现向上下伸展的分布形状,而轴向速度恰恰相反。在舵后截面上可以明显看到径向与切向速度分布呈现舵的左舷侧下方和右舷侧上方为加速域;而轴向速度虽也有上述规律,但很不明显,不过可以看到相对于舵前截面上轴向速度在截面中心部位增加不少,而在叶梢附近的却相对减小。
本文初步地探讨了采用CFD软件计算分析影响螺旋桨和舵相互干扰水动力性能的因素,对计算结果的分析尚浅显,模型的建立以及计算参数的设定还有值得改进的地方,在今后的工作中应在存在问题的地方加以改善。在进一步的考察船舶推进系统中,船体对螺旋桨、舵的影响必须加以考虑,本文的计算结果可以作为进一步计算船-桨-舵组合体的水动力性能的铺垫。
[1]中武一明.プロペラと舵の相互干涉について[J].西部造船会会报,1980,11(第61号):25-31.
[2]黄 胜.桨舵干扰的理论与实验研究[M].哈尔滨:哈尔滨工程大学出版社,1999.
[3]王福军.计算流体动力学分析-CFD软件原理与应用[M].北京:清华大学出版社,2004.
[4]王 超,黄 胜,解学参.基于CFD方法的螺旋桨水动力性能预报[J].海军工程大学学报,2008,20(4):107-112.
[5]胡 健,马 骋,黄 胜等.螺旋桨尾流场的数值分析[J].哈尔滨工程大学学报,2008,29(12):255-260.
[6]李 巍,王国强,汪 蕾.螺旋桨粘流水动力特性数值模拟[J].上海交通大学学报,2007,41(7):1020-1208.
[7]Huang sheng,Zhu xiangyuang,Guo chunyu.CFD simulation of propeller and rudder performance when using additional thrust fins[J].Journal of Marine Science and Application,2007,6(4):27-31.
[8]高富东,潘存云,蔡汶珊等.基于CFD的螺旋桨敞水性能数值分析与验证[J].机械工程学报,2010,46(8):133-138.
[9]黄 胜,王 超,王诗洋.不同湍流模型在螺旋桨水动力性能计算中的应用与比较[J].哈尔滨工程大学学报,2009,30(5):481-485.
[10]蒋少剑.螺旋桨-舵相互干扰水动力性能研究[D].上海:上海交通大学,1997.
[11]盛振邦,刘应中.船舶原理[M].上海:上海交通大学出版社,2004.

