焊接残余应力对疲劳寿命影响的定量研究

卞如冈，崔维成，万正权，李良碧，王铭伟

（1中国船舶科学研究中心，江苏 无锡 214082；2江苏科技大学船舶与海洋工程学院，江苏 镇江 212003；3空军航空大学 军械系，长春 130022）

1 引 言

众所周知，在各种焊接金属结构物中存在残余应力。残余应力是工件或结构物在其焊接加工成形过程中产生，并以平衡状态存在于其中的一种内应力。对深海耐压结构而言，在制造过程中，耐压结构的钢板需要经过下料、切割、冷弯（包括滚弯）、装配和焊接等冷热加工过程。这些加工过程造成的钢板局部冷热变化和变形均使得钢板产生不均匀的塑性变形或相变，加之结构本身的约束作用，以使耐压结构在没有外载荷作用时其内部形成一个自相平衡的残余应力场。从焊接结构的角度来说，耐压结构中的残余应力主要来源于两方面，其一是焊接热应力产生的局限于焊缝附近的、且在焊缝两边迅速衰减的焊接残余应力；其二是在焊接装配时因结构变形的约束作用而产生的约束应力。

疲劳断裂是金属结构的主要失效形式，其中焊接结构的疲劳失效表现更为突出。焊接残余应力是疲劳失效的原因之一，外部载荷和内部残余应力的双重作用通常导致焊缝区和近缝区裂纹的产生。大量研究和实践表明焊接接头的疲劳破坏一般起裂于焊接接头的焊趾部位即母材与焊缝的过渡处，如果能改善焊接接头过渡区的疲劳裂纹起裂性能将有效地提高焊接结构的疲劳强度。内部残余应力比较难于分析，因此，在以往的研究中，残余应力对疲劳寿命的影响基本上均局限于定性分析，很少给出定量的研究结果。侯维廉[1]认为在凸锥柱结合处，由于曲率改变而造成应力集中或称二次应力，焊缝的存在，焊后不能整体退火，残余应力的存在也是必然的，在循环载荷的作用，两者的叠加，从而成为疲劳破坏的敏感部位，于是得到的结论是焊接残余应力对疲劳扩展必然产生影响；黄小平[2]等人提出了一种能考虑焊趾处应力集中、焊接残余应力因素影响、受弯应力焊接结构焊趾裂纹的疲劳寿命计算方法，此方法预报的疲劳寿命与实验结果在量级上是吻合的，但在推向实用之前还需要做更多的试验验证。RRobles[3]等学者对锥柱结合处的疲劳裂纹扩展进行了研究，是将残余应力对焊接结构裂纹的影响计及到裂纹应力强度因子的计算中，没有考虑残余应力对裂纹扩展的驱动力的影响。

本文将基于双参数裂纹扩展率公式，定量计算分析残余应力对结构疲劳寿命的影响，并通过疲劳试样开展残余应力消除/降低前后的对比试验，来验证残余应力对疲劳寿命的影响作用。

2 双参数统一方法的基本理论

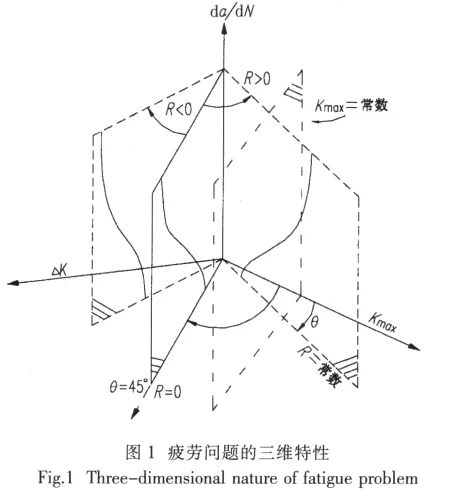
根据Sadananda和Vasudevan[4-6]提出的双参数统一理论，疲劳裂纹的扩展，需要用两个驱动力来描述，因此，就存在两个和驱动力一致的门槛值Kmax,th和ΔKth。虽然很多学者[7-12]利用双参数统一方法理论解释了各种各样特殊的疲劳现象，但没有给出一个明确的表达裂纹扩展率的公式。

1994年，Vasudevan等人[13]给出了裂纹扩展率公式：

1997年，Sadananda和Vasudevan[14]给出了裂纹扩展率公式：

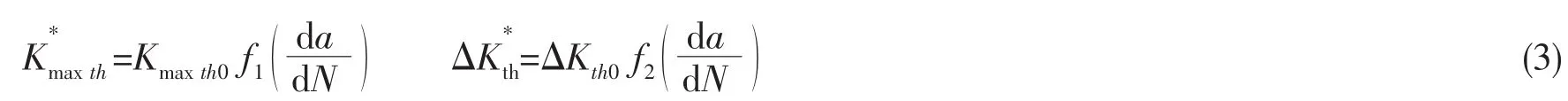
公式（1）和（2）也都是在裂纹扩展的近门槛值附近使用，并没有包括裂纹扩展的全过程，另外这两个表达式也仅仅是一般表达式，不具有太大的工程实用性。

Bukkapatnam和Sadananda[15]为描述裂纹扩展的S形曲线，提出一个扩展率公式：

其中：

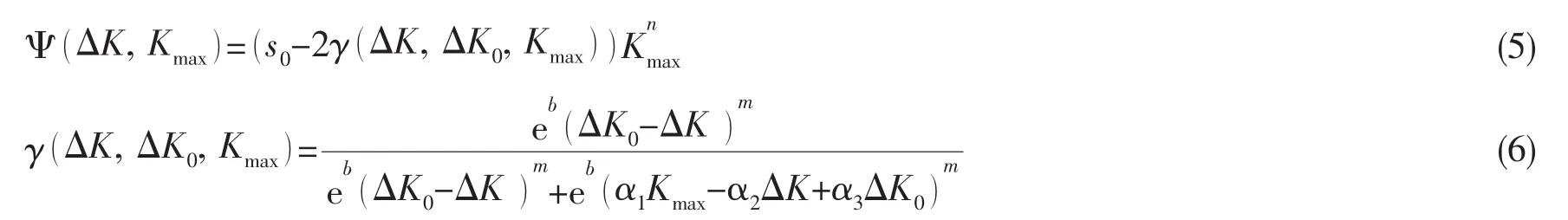
公式（4）虽然能够描述裂纹的三个扩展过程，但该公式的物理意义不清楚，完全是从数学上出发给出的一个公式。

作者们[16]提出一个能够包括裂纹扩展全过程的双参数表达式：

式中：Kmax是最大应力强度因子；ΔK是最大应力强度因子幅值；是与R有关的最大应力强度因子的门槛值；是与R有关的最大应力强度因子幅值的门槛值；Kc是断裂韧性；A，m，n，γ为材料常数；为裂纹扩展率。

3 残余应力对疲劳寿命影响的理论预报

对于深海耐压结构，其应力主要来源两方面：一是在静水外压的作用下，结构产生的弯曲应力和轴向压缩产生的膜应力；二是来自于结构在制造过程中的残余应力。本文以锥柱结合壳模型为例[17]，开展残余应力对结构的疲劳寿命影响分析。

在深海结构在下潜、上升的过程中，静水压力在其凸锥处的外表面产生较高的拉伸应力。该拉伸应力是由弯曲应力和轴向压缩产生的膜应力合成而成。如图2所示。

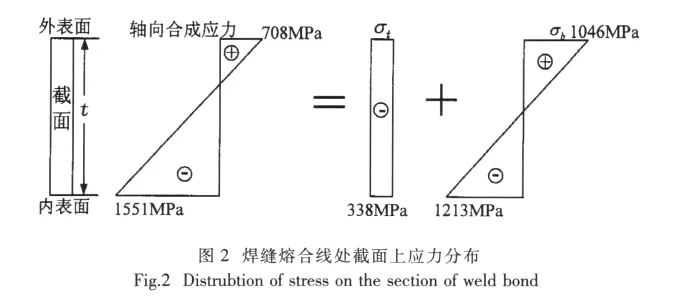
就目前对结构的疲劳问题认识而言，仍主要是拉伸应力的作用导致裂纹的进一步扩展，较高的压应力循环作用下裂纹是否扩展仍需进一步研究。基于这个原因，分析深海耐压结构的疲劳问题，主要以较高的拉伸应力部位为主。因此，不考虑残余应力的影响，对于深海耐压结构的疲劳分析，可以仅考虑正的弯曲应力的作用，不考虑负的膜应力作用，相当于：

（1） σmin=0.0 MPa；σmax=σb=1 046 MPa；

（2） 应力比 R=0.0。

结构中残余应力的存在，不仅影响结构的强度储备和弹塑性稳定性，还影响裂纹的扩展，从而导致结构的疲劳寿命下降。由于耐压结构是一个复杂的焊接结构，其内部存在一个复杂的残余应力场。残余应力是一种存在于结构中自相平衡的应力场，在交变载荷的作用，直接影响耐压结构的使用性能。在凸锥外表面焊缝熔合线处取0.3σs的残余拉应力。由于残余应力在截面上的分布不一致性，耐压壳体表面残余应力最大，逐渐向板厚方向衰减，类似于弯曲应力在截面上的分布。因此，在5.0MPa循环载荷下，计算应力强度因子时，叠加到由静水外压引起的弯曲应力上，相当于：

（1） σmin=0.3σs+0.0=258 MPa；σmax=0.3σs+σb=1 304 MPa；

（2） 应力比 R=0.197。

由此可见，目前残余应力对疲劳寿命的影响，主要是改变最大应力状态和最小应力状态，也就是改变循环应力的应力比，但没有改变循环应力幅值大小。如果按照Paris公式，只有循环应力幅值对疲劳寿命产生影响，则残余应力不会对结构的疲劳寿命有影响，但根据双参数统一理论，应力强度因子最大值对疲劳寿命也有影响，因此，残余应力是可以影响结构的疲劳寿命的。

计算过程中取初始裂纹深度a0=0.1 mm，半长度c0=1.0 mm，并假设裂纹面垂直于最大拉应力方向。联合双参数裂纹扩展率公式（7），代入高强度钢的裂纹扩展率参数[17]，计算带初始裂纹的凸锥熔合线处的疲劳扩展。裂纹深度和长度扩展计算结果a～N曲线和c～N曲线见图3。疲劳寿命的主要计算结果见表1。

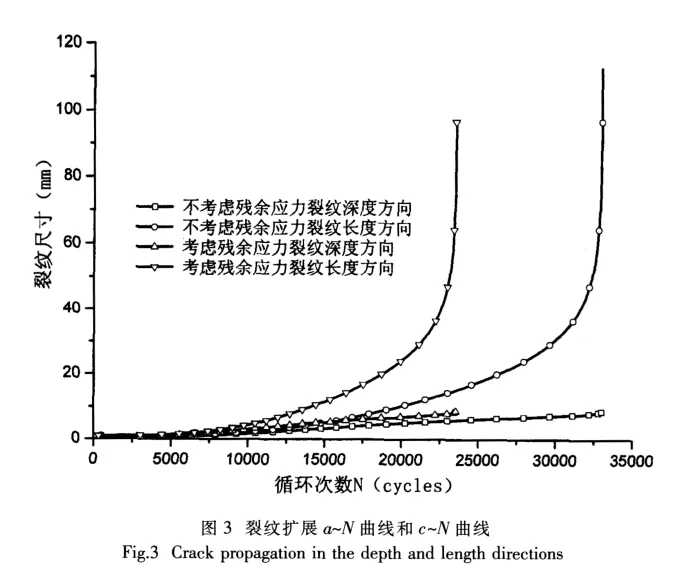
由图3和表1可以看出，残余应力没有改变裂纹的扩展趋势，明显加快了裂纹扩展的过程，大大缩短了耐压结构的疲劳寿命，影响程度大概在19.7%～40.7%之间。

表1 裂纹扩展寿命计算结果Tab.1 The calculative results of the crack propagation life

4 试验验证[18]

4.1 焊接接头几何尺寸及取样位置

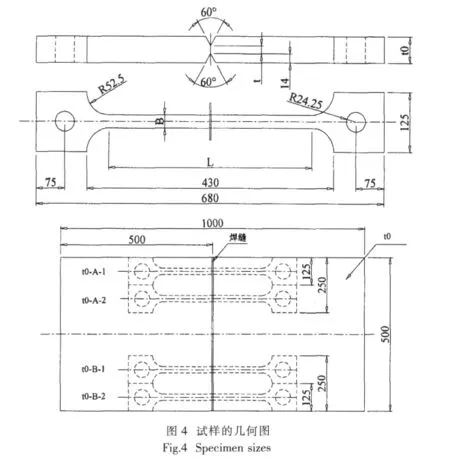
试验设计了三种不同板厚规格的试板，设置了相应的焊接工装，按照高强度钢的焊接工艺进行焊接，模拟焊接残余应力的产生。试样的具体尺寸见表2。不同厚度试样从不同厚度试板中的取样位置见图4。

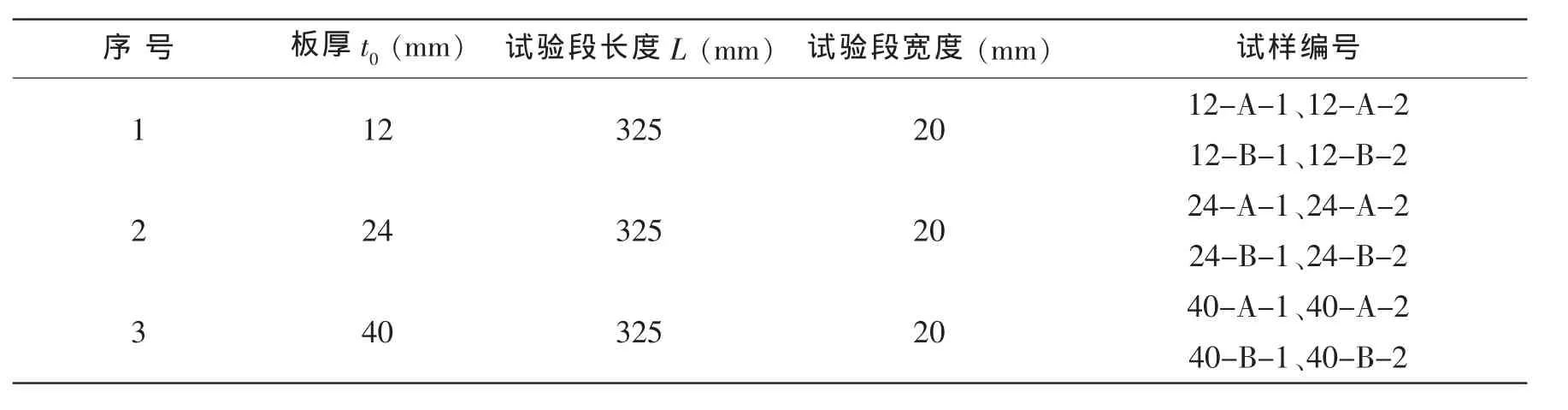
表2 试样的主要参数Tab.2 Main parameters of specimen

4.2 疲劳载荷确定

应用大型通用有限元软件ANSYS，建立高强度钢对接接头试验模型的有限元模型，如图5所示。根据试验条件，确定有限元模型的边界条件以及疲劳试验载荷。在试件的一端约束轴向位移，同时另一端施加拉伸载荷，以确定试件在疲劳试验中能达到的最大应力水平。各种不同板厚的焊接接头最大应力列表3所示，供试验参考。

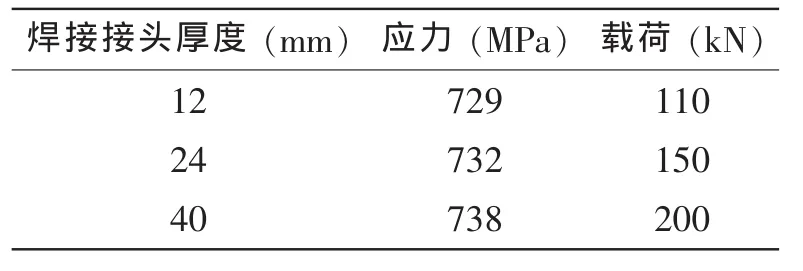
表3 确定的试验疲劳载荷Tab.3 The load of fatigue test

4.3 试验方案

试验在江苏科技大学的MTS疲劳试验系统上进行。加载波形为正弦波，加载频率为1.0 Hz，载荷比R=0.1。加载方式为轴向加载。试件的轴向加载如图6所示，左边为试件安装在试验机上的照片，右边为试件轴向加载示意图。

4.4 试验结果及分析

按照拟定方案依次进行试验，每次试件断裂后记录下循环次数。主要试验结果见表4。

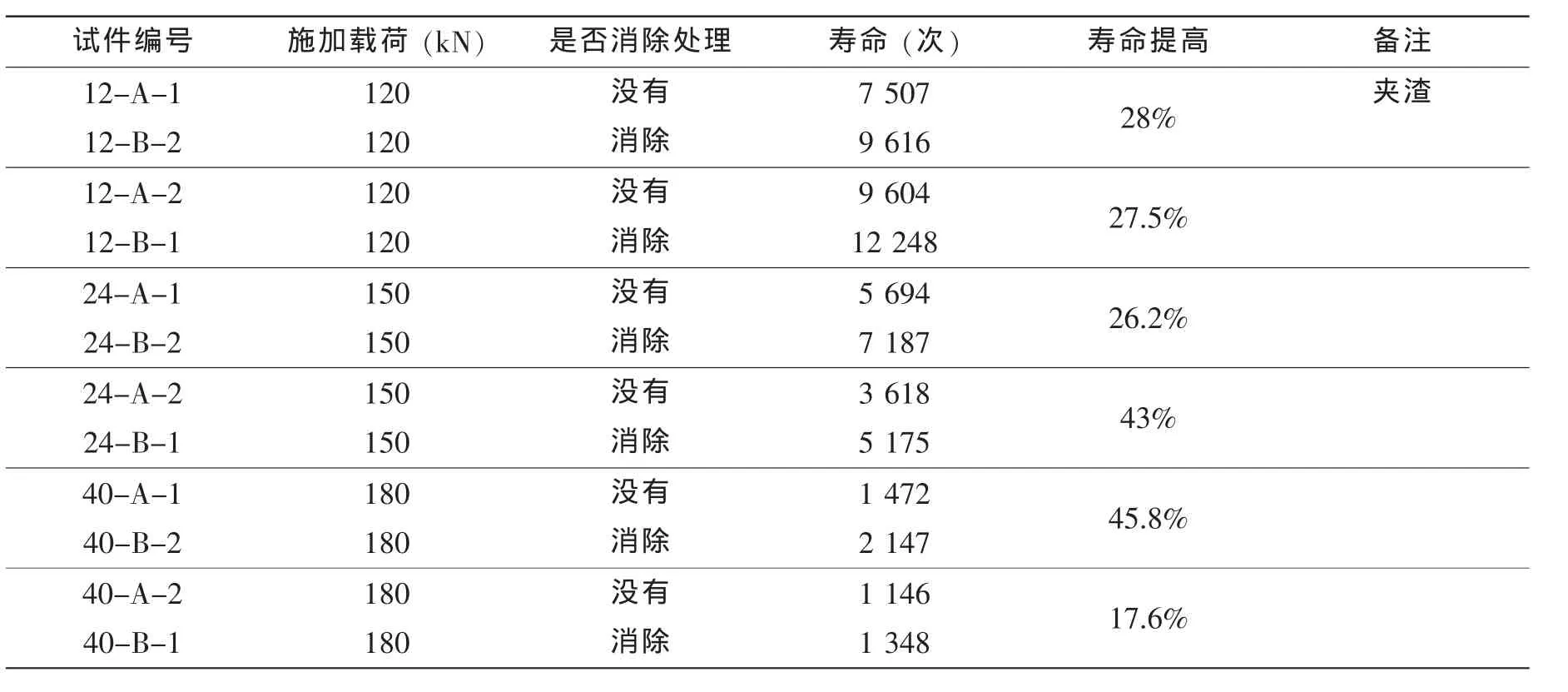
表4 疲劳寿命试验结果Tab.4 The results of fatigue tests

分析表4，对于相同板厚的试样，消除残余应力后可以明显提高试样的疲劳寿命，大概在20%到40%之间。表4的试验结果与表1的理论预报结果有很好的吻合，这说明双参数疲劳寿命预报方法能够定量地分析残余应力对疲劳寿命的影响。由于不同板厚的刚度不一样，边界反作用力也不一样，在相同焊接电流、相同焊接速度下，产生的残余应力大小不一致，消除的效果也不完全一样，因此，疲劳寿命的对比结果也不会一致，不过反映的提高疲劳寿命的规律是一样的。

从试验结果可以看出，经过超声冲击处理之后高强度钢焊接接头的疲劳寿命不同程度地有所增加，这是因为焊缝区域在焊接过程中产生较大的拉伸残余应力，在超声冲击外力作用下使得结构的残余应力重新分布，拉伸残余应力向压缩残余应力转变，提高了焊接接头的疲劳强度。

5 结 论

通过本文的理论研究和试验验证，可以得到如下结论：

（1）残余应力对焊接接头的疲劳寿命影响非常明显，理论预报和试验结果比较吻合，这说明双参数疲劳寿命预报方法能够定量地分析残余应力对疲劳寿命的影响。

（2）超声冲击消除或降低残余应力的方法可以有效提高焊接接头的疲劳寿命，大概在20%～40%之间；

（3）需要进一步开展焊接残余应力在焊接接头横剖面上的分布以及在疲劳循环载荷作用下的重新分布方式研究，这直接关系到对焊接接头处的疲劳寿命预报的准确性。

[1]侯维廉.焊接残余应力对压力容器疲劳裂纹扩展的影响[J].压力容器,1996,13(2):116-118.

[2]黄小平,崔维成,石德新.潜艇锥柱结合壳焊趾表面裂纹疲劳寿命计算[J].船舶力学,2002,4(8):62-681.

[3]Robles L B R,Buelta M A,Goncalves E,Souza G F M.A method for the evaluation of the fatigue operational for submarine pressure hulls[J].International Journal of Fatigue,2002,22:41-52.

[4]Vasudevan A K,Sadananda K.Application of unified fatigue damage approach to compression-tension region[J].International Journal of Fatigue,1999,21(s1):s263-s273.

[5]Vasudevan A K,Sadananda K,Glinka G.Critical parameters for fatigue damage[J].International Journal of Fatigue,2001,23:s39-s53.

[6]Sadananda K,Vasudevan A K.Crack tip driving forces and crack growth representation under fatigue[J].International Journal of Fatigue,2004,26:39-47.

[7]Bukkapatnama S T S,Sadananda K.A genetic algorithm for unified approach-based predictive modeling of fatigue crack growth[J].International Journal of Fatigue,2005,27:1354-1359.

[8]Maymon G.A ‘unified’ and a(ΔK+.Kmax)1/2crack growth models for aluminum 2024-T351[J].International Journal of Fatigue,2005,27:629-638.

[9]Maymon G.Probabilistic crack growth behavior of aluminum 2024-T351 alloy using the ‘unified’ approach[J].International Journal of Fatigue,2005,27:828-834.

[10]Zhang J,He X D,Du S Y.Analyses of the fatigue crack propagation process and stress ratio effects using the two parameter method[J].International Journal of Fatigue,2005,27:1314-1318.

[11]Stoychev S,Kujawski D.Analysis of crack propagation using ΔK and Kmax[J].International Journal of Fatigue,2005,27:1425-1431.

[12]Noroozi A H,Glinka G,Lambert S.A two parameter driving force for fatigue crack growth analysis[J].International Journal of Fatigue,2005,27:1277-1296.

[13]Vasudeven A K,Sadananda K,Louat N.A review of crack closure,fatigue crack threshold and related phenomena[J].Materials Science and Engineering A,1994(A188):1-22.

[14]Sadananda K,Vasudevan A K.Crack tip driving forces and crack growth representation under fatigue[J].International Journal of Fatigue,2004,26:39-47.

[15]Bukkapatnama S T S,Sadananda K.A genetic algorithm for unified approach-based predictive modeling of fatigue crack growth[J].International Journal of Fatigue,2005,27:1354-1359.

[16]Cui W C,Bian R G,Liu X C.Application of the two-parameter Unified Approach for Fatigue Life Prediction of Marine Structures[C].PRADS2007,2007:392-398.

[17]卞如冈.高强度钢潜艇结构低周疲劳特性研究[D].无锡:中国船舶科学研究中心,2010.

[18]卞如冈.耐压船体焊接试样对比试验报告[R].无锡:中国船舶科学研究中心科技报告,2009.