考虑蠕变特性的斜坡堤软土地基变形数值分析＊

葛栋林,史宏达

(1.中国海洋大学,山东 青岛 266100;2.海军工程设计研究院,北京 100070)

海岸工程中,抛石斜坡堤结构对地基的沉降变形适应性较强,常用于地质条件差、软土层厚的围港工程建设。一般来说,堤底的软土在施工期和工后会发生较大的沉降与侧向位移,对分级加载施工中各级抛填预留沉降量产生影响,需要对这一问题进行深入分析。目前,在对结构荷载作用下软土地基变形的数值研究中,较少考虑软土的蠕变特性对长期变形的影响,而可能低估了地基软土层部分的变形水平。因此,为准确预测斜坡堤软土地基变形量,有必要在数值分析中采用能够反映土体变形时间效应的本构模型[1-3]。

本研究采用Plaxis二维有限元程序,针对某防波堤工程典型断面的地基软土层分别采用摩尔-库仑理想弹塑性模型(Mohr-Cou lom b Model)和软土蠕变粘弹塑性模型(Soft-Soil-Creep Model)进行模拟,对比分析了施工期和工后的软土地基变形特点,初步得到了几点结论。

Plaxis程序是荷兰Delft科技大学开发的著名的岩土工程有限元软件,可以进行变形、固结、分级加载、稳定、渗流、动力等类型的计算,尤其适用于软土的变形和稳定分析[4]。该程序提供了多种岩土材料本构模型,包括摩尔—库仑模型和软土蠕变模型,采用比奥固结理论对土体进行固结计算。

1 本构模型

1.1 摩尔-库仑模型

该模型采用摩尔-库仑破坏准则判别土体是否破坏。一旦土体内任意平面上的剪应力达到了土的抗剪强度,土体就发生破坏,而任意平面上的抗剪强度只是该平面上法向应力的函数[4-5],即：

式中,c和φ为强度参数。

摩尔-库仑模型参数包括：天然容重γunsat、饱和容重γsat、杨氏模量E、泊松比μ、粘聚力c、内摩擦角φ、剪胀角 Ψ。

1.2 软土蠕变模型

描述土体应力应变一般状态的三维软土蠕变模型比较复杂,但是由一维蠕变微分法则推广得到。本研究仅给出一维蠕变微分表达式。它基于修正的剑桥模型,根据Buism an和Butterfield最初提出的蠕变公式,经过推导,可得最终蠕变公式[4-6]：

软土蠕变模型具有与摩尔-库仑模型相同的强度破坏参数,即粘聚力c、内摩擦角 φ、剪胀角 Ψ;基本刚度参数有修正压缩指数λ＊、修正膨胀指数κ＊、修正蠕变指数μ＊,这些参数既可以通过等向压缩试验得到,也可以通过固结仪实验得到;高级参数程序推荐使用缺省值,有卸载-再加载泊松比υur、正常固结状态的应力比KNC0 、相关参数M。

2 有限元模型建立

2.1 工程概况

如图1所示,该抛石斜坡堤施工海域地基条件较差,海底表层存在约10m厚的淤泥质粉质粘土层,下层依次为粉质粘土层和砂层。地基处理方案采用清除软土表层约2 m厚浮泥回填中粗砂做垫层,垫层与堤心石间铺设一层土工格栅。由于堤底仍然保留了约8m厚的软土层,在满足边坡稳定性要求前提下,需要准确估计软土层的变形量来指导施工预留沉降量。

图1 斜坡堤典型断面示意图Fig.1 Sketch show ing a typical cross section of a sloping breakw ater

2.2 模型建立

在有限元模型中(图2),护面块体简化为等效竖向分布荷载。土工格栅采用程序提供的土工格栅模型,其本构关系简化为线弹性,视为只能沿轴向变形的一维单元,轴向抗拉强度参数EA=105kN/m;用界面单元模拟土与土工格栅的相互作用,两者变形一致没有相对滑动,摩擦系数R inter=1.0。对淤泥质粉质粘土层分别采用摩尔-库仑模型和软土蠕变模型模拟,堤心石、粉质粘土和砂层均采用摩尔-库仑模型模拟。软土蠕变模型的基本刚度参数值由试验数据得到,分别为λ＊=0.09、κ＊=0.015、μ＊=0.006,各土体材料物理力学指标及计算参数见表1。

表1 各土体材料物理力学指标及计算参数Table 1 Dynam ic indexes and calcu lation parameters for various soils

图2 有限元计算模型示意图Fig.2 Sketch for FEM model

选择平面应变计算类型;采用15节点的三角形单元自动划分网格,全局疏密度设置为中等,堤底软土层局部加密;计算区域为海底面下50m的深度和距离防波堤中心线左右各120m的水平范围;上边界透水自由,两侧边界不透水且水平固定竖向自由,底边界透水且水平和竖向均固定。

模型计算内容为：首先,对全部土体采用摩尔-库仑模型模拟斜坡堤施工和服役期间地基土体变形和超静孔压的生成和消散过程;其次,仅对淤泥质粉质粘土层采用软土蠕变模型重复上述模拟过程。由于地基土体变形较大,两次计算都需要进行网格更新和孔隙水压力更新计算,考虑几何二阶变形效应和沉降引起的堤心石有效重量的减小,从而更真实地反映土的沉降[4]。简化的斜坡堤施工过程见表2。

表2 简化的施工过程Table 2 Main stages simp lifying the engineering process

3 模型计算结果分析

摩尔-库仑模型可视作反映土体应力应变关系的一阶近似弹塑性模型,软土蠕变模型可视为二阶近似粘弹塑性模型[4]。因此,可将同一地基软土采用两种模型模拟出现的变形数值差异粗略视为由该软土蠕变行为导致。

比较软土地基最终网格变形图(图3),可以看出两种模型计算得到的软土地基最终变形趋势大体一致,堤中心最大,向两侧逐渐减小,但采用摩尔-库仑模型计算的变形量要小于软土蠕变模型的结果,且前者发生变形区域基本限制在堤底土体范围内,后者至少还在堤身两侧有限元模型范围内产生一定的沉降(图3)。

通过图4对比可以更直观看出两种模型在横剖线A-A＊(图3)上得到的最终变形差别。摩尔-库仑模型计算的变形量极大值位于剖线中间点为0.69m,从变形轮廓线看,由堤中心向两侧逐渐收缩,曲率亦逐渐变小,在堤坡脚附近变形量和曲率趋近于零,呈典型的弓形状;软土蠕变模型计算的变形量极大值亦在剖线中间点为1.05 m,变形轮廓线亦由堤中心向两侧逐渐收缩,但曲率有变大趋势,在堤坡脚附近变形近乎水平且曲率达到最大,近似呈U形状。两者比较来看,堤中心变形差异小于坡脚附近差异,前者主要体现在竖向沉降量上,后者主要体现在水平位移量上。如前所述,可以认为剖线中间点蠕变引起的沉降量约为0.36 m,约占总沉降量的34%。

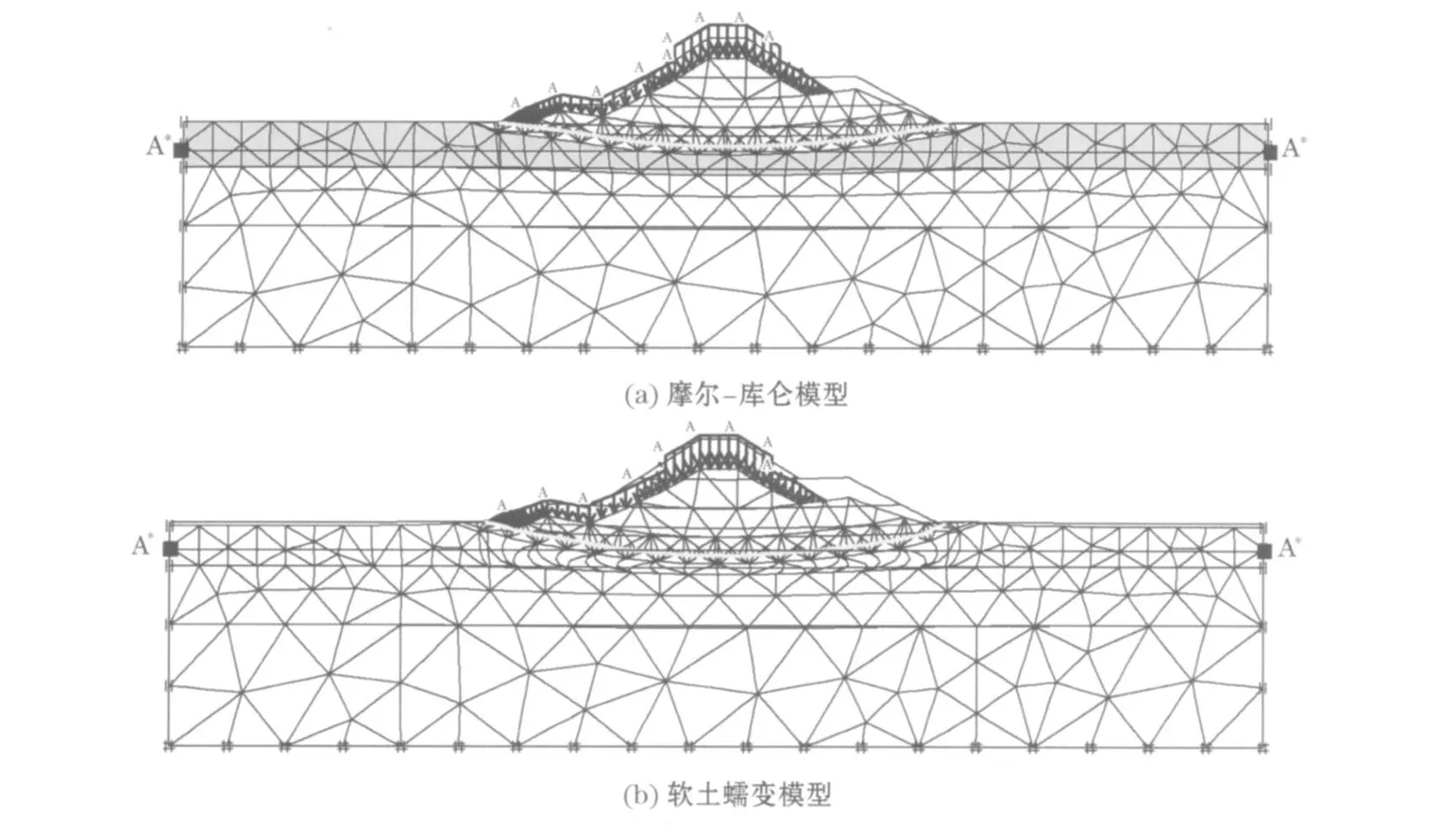
图3 最终网格变形比较(放大5倍)Fig.3 Comparison of finalmesh deformation between the two models(5 times enlarged)

图4 堤底软土层中部横剖线上点的最终位移比较(放大20倍)Fig.4 Comparison betw een the tw omodels of final displacement of the relevant points on the section in them idd le of soft soil layer under the breakw ater(20 times enlarged)

由图5可见,两种模型计算的B点(图2)沉降量在施工初期的差别不大,进入施工后期两者计算的沉降曲线产生分化。摩尔-库仑模型计算的曲线下降速率减慢,逐渐趋于稳定,大约工后5 a完成固结,最终沉降量为1.03m;此时软土蠕变模型计算曲线尚未稳定,仍在缓慢发展,表现出较明显的次压缩特点,模型预测约工后18 a沉降曲线趋于水平,沉降量为1.48m。B点蠕变引起的沉降量约0.45 m,占总沉降量的30%。

图6表明从第2施工阶段即抛填第一级堤心石开始,摩尔-库仑模型计算的C点(图2)超静孔压较软土蠕变模型计算结果要小,尤其在加载过程中前者超静孔压增长速率远小于后者。最大超静孔压发生在第4施工阶段结束时,摩尔-库仑模型计算值为-152.5 kPa,软土蠕变模型计算值为-204.4 kPa。这是因为软土蠕变模型考虑了不排水加载过程中由于土体蠕变收缩引起的平均有效应力减小[4]。

比较发现,摩尔-库仑模型计算的C点超静孔压消散过程与本模型计算的B点固结沉降过程一致;软土蠕变模型计算的C点超静孔压绝大部分消散在摩尔-库仑模型计算的固结期内,但仍有约2%消散速率极其缓慢,这一特点与本模型计算的B点漫长的次固结压缩过程相应。

图7所示堤内坡脚软土层中部D点(图2)侧向位移发展过程与B点沉降过程类似,不同的是软土蠕变模型计算结果要远远大于摩尔-库仑模型的计算结果,前者最终侧向位移为0.60m,后者为0.19 m。D点蠕变引起的侧向位移量达0.41m,占总侧向位移量的68%。从摩尔-库仑模型计算曲线看,工后固结期间有恢复侧向变形的趋势,这是不符合实际情况的。

图7 堤内坡脚下软土层中部D点侧向位移变化曲线比较Fig.7 Comparison betw een lateral displacement curves for Point D in themidd le o f soft soil layer under the insidemargin of the breakw ater

4 结 论

1)本次研究结果表明：采用软土蠕变模型模拟地基软土层较摩尔-库仑模型,斜坡堤地基工后变形量大,不少于30%;软土层变形至稳定和超静孔压消散完全的历时漫长,需要近20 a。该结果基本与现有类似工程研究成果[1-7]一致,可以供该斜坡堤分级加载施工时参考。

2)由于软粘土有显著的蠕变特性,在利用数值方法研究抛石斜坡堤结构下的软土地基变形量时,需要采用能反映这一特性的本构模型以增强预测结果的可靠性。Plaxis程序提供的软土蠕变模型基于严密的数学模型预测和三轴试验数据,并经国内外一些工程实践的检验,可以近似描述软土的蠕变特性。

3)在未设置人工排水通道的深厚软土地基斜坡堤设计与施工过程中,需要充分考虑饱和软粘土的蠕变特性及其可能的影响,以保证堤体的安全稳定,确定合理的加载预留沉降量和堤顶高程。

[1] 朱强,张惠明.考虑蠕变特性的软土路堤沉降有限元分析[J].盐城工学院学报：自然科学版,2007,20(1)：64-67.

[2] 于秀梅,肖军华,范春青.路堤荷载下软土地基蠕变变形性状预测及分析[J].国防交通工程与技术,2007,5(4)：29-32.

[3] 吴凤亮,李伟.箱筒型基础防波堤结构的沉降量分析[J].国防交通工程与技术,2006,4(4)：39-42.

[4] BRINKGREVE R B J,VERM EER P A.PLAXIS version 8.2 Manual[M].Rotterdam：A A Ba lkema,2002.

[5] 陈文苏.软土蠕变沉降的数值模拟[D].天津：天津大学建筑工程学院,2004.

[6] VERMEER P A,NEHER H P.A soft soilmodel that accounts for creep[C]∥Beyond 2000 in Computational Geotechnics-10 Years of PLAXIS International.Balkema：Rotterdam,1999：1-13.

[7] 夏小兵,李光范,续建新.筑堤地基的粘弹塑性分析[J].山西建筑,2010,36(7)：363-365.