贝克利数对圆管流道交变流动传热的影响分析

汤 珂 唐文涛 张 玙 金 滔 林小钢 雷 田

(1浙江大学制冷与低温研究所 杭州 310027)

(2中国科学院理化技术研究所低温工程学重点实验室 北京 100190)

1 引言

回热式低温制冷机(例如:斯特林制冷机、GM制冷机、脉管制冷机等)以流体工质交变流动为基本特征。在交变流动中，流体工质反复流经传热表面与之换热，与通常单一方向流动的传热特性显著不同。交变流流动的传热特性是深入理解回热式低温制冷机工作原理，以及实现其精确设计的重要基础。而目前，对于管内交变流动传热的研究不足。

美国麻省理工学院Dean，Smith等人针对斯特林热机中出现的交变流动及传热现象，开展了管内交变流动传热的实验研究。考察了交变频率、测试管道两端所连接的压缩机活塞之间的相位角对于传热的影响，给出第一阶和第二阶努塞尔数与贝克利数的经验关联式［1－3］。克里夫兰州立大学 Kannapareddy 等针对斯特林热机中回热器、冷却器以及加热器内的交变流动传热现象进行了数值模拟研究［4］。研究结果中，以管壁温度和流体混合平均温度的差值作为温差来求得无量纲换热系数努塞尔数，在流体流动反向的时刻会出现努塞尔数趋于无穷大的情况。香港科技大学Zhao等研究圆管内不可压缩层流交变流动传热，采用时空平均努塞尔数来表征传热的结果，主要考察无量纲流体位移振幅以及动态雷诺数对于时空平均努塞尔数的影响，并给出了相应的经验关联式［5］。

目前，对于管内交变流动和传热特性的研究，主要是针对不可压缩流体［4－6］。而以色列理工学院Garaway等的研究指出气体工质的可压缩性将显著影响压力、速度间的相位角与交变频率间的相关性［7］。为此，本文通过数值模拟研究圆管内可压缩层流交变流动传热现象。采用离散傅立叶级数的表达形式表征管内交变流动传热特性。根据前人的研究工作［1－3］以及对管内可压缩交变流动传热相似准则体系的分析［8］可知，贝克利数其中:ω为角频率，Dh为管道水力直径，α为热扩散系数。)是描述交变流动传热的关键相似准则。因此本文重点考察贝克利数对于管内可压缩层流交变流动传热特性的影响，计算分析了0阶努塞尔数(即时均努塞尔数)随贝克利数的变化关系。

2 控制方程

可压缩黏性流体非定常流动(忽略体积力、无内热源)的一般控制方程［9］如下:

连续性方程:

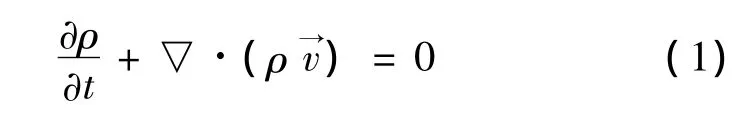
动量方程:

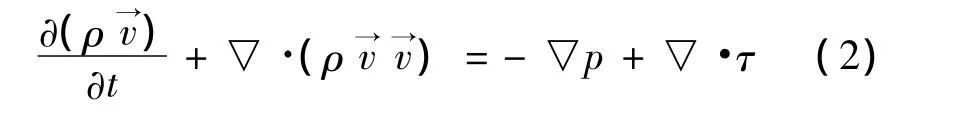
能量方程:

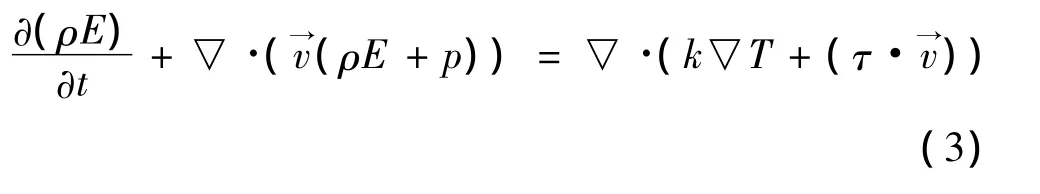
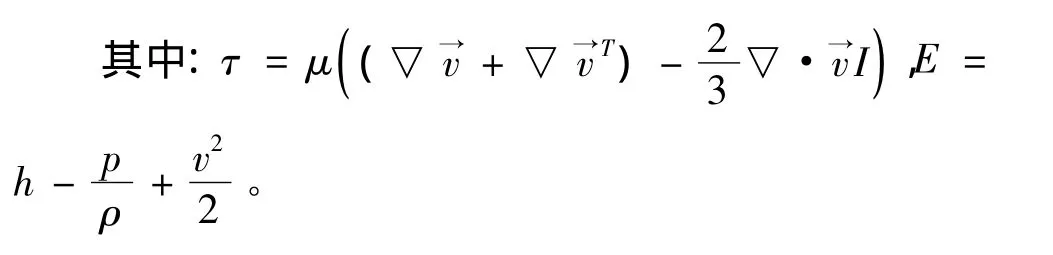
3 计算模型

计算模型为内径1 mm的圆管流道。文献［10］等针对管内不可压缩层流交变流，推导了热发展段的长度Ld的表达式。根据该研究结果，在计算模型中，将管长选定为3倍热发展段长度，以使得所关注的管道轴向中心位置处于充分发展区。

流道左端设为随时间做正弦变化的质量流入口，温度恒定为330 K。右端为随时间做正弦变化的压力出口，操作压力为2.0 MPa，流体工质为氦气，温度恒定为330 K。通过调节质量流入口和压力出口的相位和幅值使得观测点(流道轴向中心位置处)的速度和压力的相位差为0，最大雷诺数为650，压比为1.2。管壁温度保持300 K。采用二维轴对称计算模型，整个计算区域轴向网格情况为50/mm，径向网格数为50，壁面附近的流体网格加密。时间步长取为交变周期的1/180。利用FLUENT软件进行求解，压力/速度耦合采用SIMPLE算法，时间迭代采用一阶隐式算法。

根据脉管制冷机、热声热机等回热式热机换热器内的实际工况，确定贝克利数的研究范围为2到300。研究对象是管内层流交变流，依据Hino等对于管内交变流湍流转变的研究结果［11］，将最大雷诺数(Remax=umaxDh/ν，umax为最大速度，对于正弦规律变化情况即为速度振幅，ν为运动粘度)选定为650，以保证流动状态为层流。

对模拟计算进行了稳定性判定。当计算进行到第11个周期及以后，流道中心点速度振幅、温度振幅及压力振幅的相对变化率小于1%，认为数据已基本稳定，取第11个周期的数据。同样针对网格独立性也进行了相应的考察。对于计算中所采用的网格，分别将网格在径向和轴向加倍后，监测研究中所关心的物理量，如流道中心点速度振幅、压力振幅、温度振幅等参数，各物理量的相对变化率均小于3%。

4 计算结果与讨论

4.1 管内交变流动传热性能的表征

管内交变流动传热过程中，流道中心流体与管壁的温差以及壁面处的热流密度均为周期变化，如果简单地根据牛顿冷却定律将壁面处的热流密度除以中心流体与管壁的温差来获取瞬时的传热系数可能出现由于中心流体与管壁的温差趋近于零而导致换热系数无穷大的情况。关于管内交变流动传热性能的表征，香港科技大学Zhao等采用时空平均努塞尔数，其中流体的温度采用测试管段两端的混合室中气体的周期平均温度，而壁面温度取4个轴向位置测点温度时均值的平均值，无法反映周期内的变化情况［12］。法国南特大学Bouvier等通过各阶谐次累加的热流密度和壁面温度与截面平均温度的差值来计算的无量纲换热系数［13］，能够反映周期内的变化情况，但测量截面流体平均温度及基于反传热方法获得壁温等都非常困难，精度难以保证。

参考麻省理工学院Dean，Smith等的研究思路，采用多阶努塞尔数表征管内交变流动传热性能［1－3］。具体而言，将模拟计算获得的流道中心流体与管壁的温差和壁面处的热流密度的周期变化均表达为离散傅立叶级数形式，根据牛顿冷却定律得到各阶对流换热系数，然后将其表达为无量纲的各阶努塞尔数。其中第0阶表示时均传热情况，而从一阶开始的以后各阶共同反映周期内的波动情况。例如:首先将流道中心流体与管壁的温差和壁面处的热流密度的周期变化表达为离散傅立叶级数形式，如下所示:

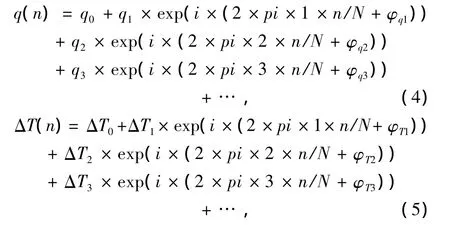
其中:N为一个流动周期内流道中心流体与管壁的温差和壁面处的热流密度的数据点数，然后求解各阶传热系数，即 hm=qm/ΔTm(m=0，1，…，N/2)，最后由 Num=hmDh/k(m=0，1，…，N/2)求得各阶努塞尔数。

图1和图2给出了流道中心流体与管壁的温差和壁面处的热流密度分别采用三阶、四阶以及五阶级数表达式拟合的数据。采用式(6)计算一个周期内拟合值与模拟计算的原始数据的相对误差:

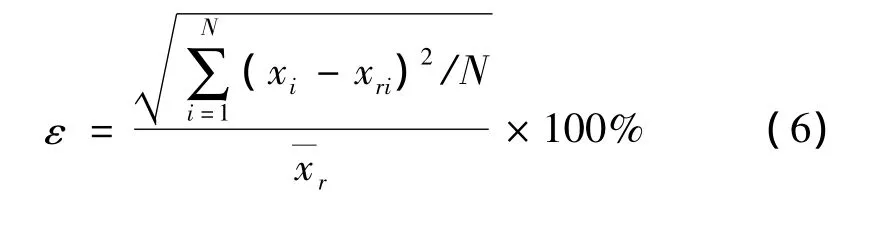
式中:xi为一个周期内第i个时刻的级数拟合值;xri表示由模拟计算得到的一个周期内第i个时刻的原始数据;x—r则表示原始数据的周期平均值。通过将各阶拟合值与模拟计算所得的原始数据对比发现，当采用五阶级数拟合时，温差和热流密度的拟合值与计算所得的原始数据的相对误差均可小于10%，能够较好地反映原始数据的变化情况。

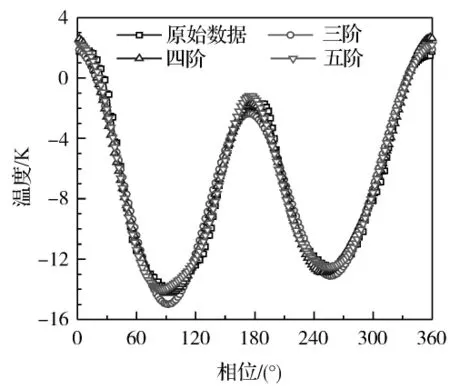
图1 傅立叶级数拟合值与温差原始计算数据的比较Fig.1 Comparison between the fitting values with discrete Fourier series and the computed temperature difference

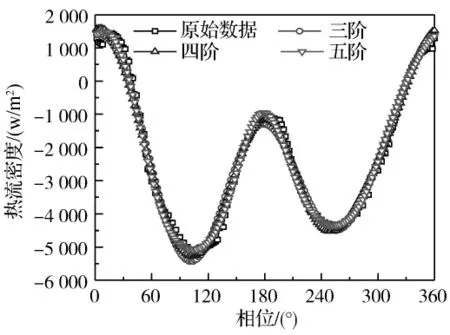
图2 傅立叶级数拟合值与热流密度原始计算数据的比较Fig.2 Comparison between the fitting values with discrete Fourier series and the computed heat flux

4.2 管内交变流动传热特性

首先，给出贝克利数对一个周期内交变流动传热过程影响的有代表性计算结果。图3和图4给出了贝克利数等于2时，计算管段轴向中心位置一个流动周期内流道截面中心点的静压和速度以及流道截面中心点的温度和壁面处热流密度的变化情况。图5和图6对应给出的是贝克利数为300时的情况。结果显示，在两种贝克利数下，流道中心点的温度和壁面处的热流密度随时间的变化呈现不同的变化规律。如图4所示，当贝克利数较小时，在一个流动周期内，流道中心点的温度和壁面处的热流密度会出现两个峰值，与2005年法国南特大学Bouvier等［13］报道的实验测量观察到流体温度信号2倍于流体运动频率的情况相符;而当贝克利数较大时，流道中心点的温度和壁面处的热流密度则与静压和速度是同频率变化的，如图6所示。可见，贝克利数对于管内交变流动传热会存在显著的影响。贝克利数的物理意义是:热扩散的时间尺度与交变周期之比。当贝克利数较小时，热扩散的时间相对于交变周期来说很短，壁面处的传热足以通过径向扩散影响到流道中心的温度，因此在一个流动周期中，流体往复两次反向的流动传热过程导致流道中心处温度信号出现2倍于交变流动频率的情况。而当贝克利数较大时，热扩散的时间相对于交变周期而言很长，也即热量还来不及扩散到管道中心处，流体已经流过该传热面，流体虽然也是两次流经传热面，但是流道中心温度受壁面传热的影响小，其变化主要源于压力的波动，因此保持与交变流动频率一致。

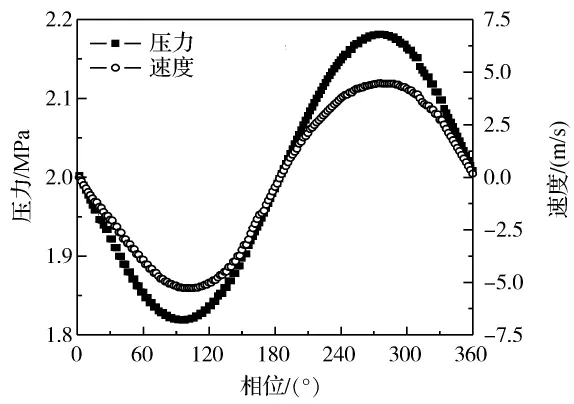
图3 流道中心点的静压和速度，Peω=2Fig.3 Pressure and velocity at the channel center，Peω =2

在实际换热器的设计中，主要关注的是周期平均换热效果，因此进一步考察时均努塞尔数(即第0阶努塞尔数)随着贝克利数的改变而呈现的变化规律。计算结果示于图7。从图中可以看出，在设定最大雷诺数为650的条件下，当贝克利数小于20时，时均努塞尔数基本不随贝克利数变化;而当贝克利数在20到300范围内时，时均努塞尔数则随贝克利数增大呈现增大的趋势。可见，当贝克利数较大时，其对交变流动传热的影响更为显著。

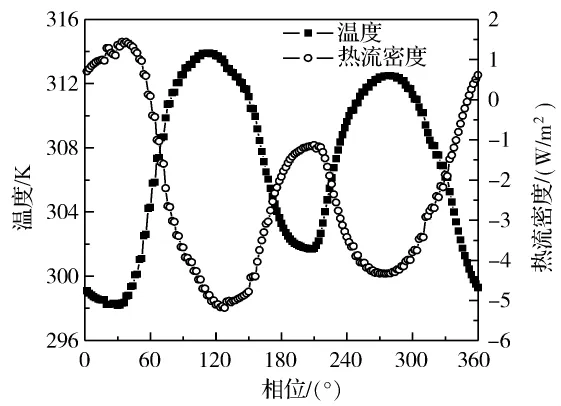
图4 流道中心点的温度和壁面处热流密度，Peω=2Fig.4 Temperature at the channel center and heat flux at wall，Peω =2

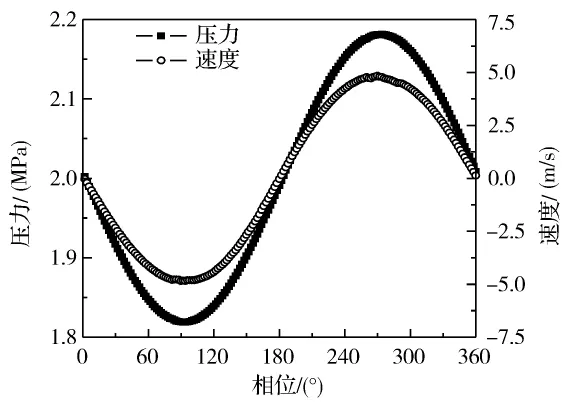
图5 流道中心点的静压和速度，Peω=300Fig.5 Pressure and velocity at the channel center，Peω =300

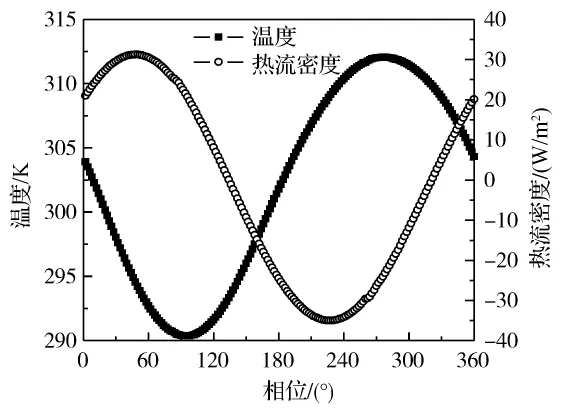
图6 流道中心点的温度和壁面处热流密度，Peω=300Fig.6 Temperature at the channel center and heat flux at wall，Peω =300

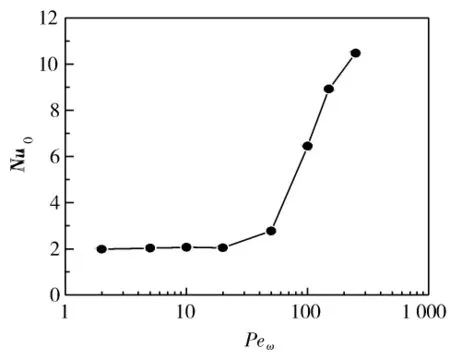
图7 时均努塞尔数随贝克利数的变化Fig.7 Time-averaged Nusselt number as a function of Peclet number

5 结论

根据可压缩黏性流体的一般控制方程，通过数值模拟研究了管内交变流动传热特性，重点考察贝克利数对于交变流动传热的影响，得出以下结论:

(1)采用离散傅立叶级数形式表达流道中心流体与管壁的温差以及壁面处热流密度时，取至五阶级数拟合可与原始数据的相对误差小于10%，能够较好地反映原始数据的变化情况。

(2)在本文分析条件下，当贝克利数较小时(如贝克利数等于2)，在一个流动周期内，流道中心点的温度和壁面处的热流密度均会出现2个峰值，即这2个参数的变化2倍于交变流动的频率;当贝克利数较大时(如贝克利数等于300)，在一个流动周期内，流道中心点的温度和壁面处的热流密度则与流体的静压和速度保持同频率变化。

(3)在本文分析条件下，当贝克利数小于20时，时均努塞尔数几乎不随贝克利数变化;而当贝克利数在20到300的范围内，时均努塞尔数则随着贝克利数的增长而增大，即在贝克利数较大时，其对交变流动传热的影响更为显著。

1 Dean C E.Establishing baseline data for an experimental apparatus that measures heat transfer under conditions of oscillating pressure and flow［D］.Cambridge:Massachusetts Institute of Technology，1993.

2 Grassmyer W A.Experiments in heat transfer under conditions of oscillating pressure and flow［D］.Cambridge:Massachusetts Institute of Technology，1994.

3 Cheng P D L.Experiments in heat transfer under conditions of oscillating pressure and flow［D］.Cambridge:Massachusetts Institute of Technology，1995.

4 Kannapareddy M R.Numerical thermal analysis of heat exchangers for the Stirling engine application［R］.NASA－CR－199120，1995.

5 Zhao T S，Cheng P.A numerical solution of laminar forced convection in a heated pipe subjected to a reciprocating flow ［ J］.International Journal of Heat and Mass Transfer，1995，38(16):3011－3022.

6 Jaworski A J，Mao X A，Mao X R，et al.Entrance effects in the channels of the parallel plate stack in oscillatory flow conditions［J］.Experimental Thermal and Fluid Science，2009，33(3):495－502.

7 Garaway I，Grossman G.Studies in high frequency oscillating compressible flow for application in a micro regenerative cryocooler［C］.Advances in Cryogenic Engineering:Transactions of the Cryogenic Engineering Conference，2006，823:1588－1595.

8 汤 珂，张 玙，林小钢，等，交变流动传热的相似准则［J］，低温工程，2010(2):4－7.

9 Anderson J D.Computational Fluid Dynamics［M］.New York:McGraw－Hill Inc，1995.

10 Lee D Y，Park S J，Ro S T.Heat transfer in the thermally developing region of a laminar oscillating pipe flow ［ J］.Cryogenics，1998，38(6):585－594.

11 Hino M，Sawamoto M，Takasu S J.Experiments on transition to turbulence in an oscillatory pipe flow ［ J］.Journal of Fluid Mechanics，1976，75(2):193－207.

12 Zhao T S，Cheng P.Oscillatory heat transfer in a pipe subjected to a laminar reciprocating flow ［ J］.Journal of Heat Transfer，1996，118(3):592－597.

13 Bouvier P，Stouffs P，Bardon J P.Experimental study of heat transfer in oscillating flow ［ J］.International Journal of Heat and Mass Transfer，2005，48(12):2473－2482.