基于dSPACE平台的稳瞄控制系统建模方法研究

胥青青，吴玉敬，张璟玥，姜世洲

(西安应用光学研究所，陕西 西安710065)

机载光电稳瞄系统常常要将光电传感器(电视、红外和激光测距机)的视轴精确指向目标，以完成对目标的捕获、跟踪及测量，配合武器系统，完成对目标的精确打击。机载光电稳瞄伺服控制系统是机载光电稳瞄系统的重要组成部分，用来隔离载体的扰动，保证光电传感器的视轴在惯性空间的稳定。伺服控制系统的性能决定了机载光电稳瞄系统的整体作战效能。

对象模型是进行控制系统设计的基础，模型建立的精确程度会直接影响控制系统设计效果。传统的建模方法是物理建模法，该方法首先建立理论模型，然后对其中的参数进行计算、测量和估算，最终得到控制对象的模型，但实际建模过程中往往存在控制对象某些参数难以实际测量，结构体谐振、轴系摩擦和线缆扰动等非线性因素难以准确估算等问题，最终导致建立的模型和实际系统差别很大。本文提出一种频域建模方法，该方法通过对控制系统进行扫频，然后采用最小二乘拟合方法对数据进行处理，获得对应于该系统的频率特性数据，通过MATLAB 中的Ident 工具箱辨识频率特性数据，获得与该频率特性数据拟合精度较好地一个传递函数，对该传递函数前向通道和反馈通道进行分离，前向通道的传递函数较好地反应了实际稳瞄系统的模型。在该模型基础上，本文还利用SISO 控制系统设计工具箱设计了速率稳定回路控制器，取得了较好的控制效果。

1 基于dSPACE 平台的建模方法

基于dSPACE 半实物仿真平台的建模主要用dSPACE 和MATLAB 实现，具体分为2 步:1)对控制对象扫频后采用最小二乘法拟合频率特性;2)利用MATLAB下的Ident 系统辨识工具箱辨识对象数学模型。

1.1 dSPACE 系统简介

dSPACE 半实物仿真平台是由德国dSPACE 公司开发的一套基于MATLAB/Simulink 的控制系统在实时环境下的开发及测试工作平台，实现了和MATLAB/Simulink 的无缝连接。dSPACE 由2 部分组成:1)硬件系统，2)软件环境。

dSPACE 硬件系统的主要特点是具有高速计算能力，包括处理器和I/O 接口等;本系统采用的硬件配置板卡包括处理器板DS1005、AD 转换板DS2002和DA 转换板DS2103.

dSPACE 软件环境具有强大的功能，可以很好地完成控制算法的设计、测试和实现，可以方便地实现代码生成/下载和试验调试等工作。dSPACE 软件环境主要由MATLAB/Simulink 和ControlDesk 组成。激励信号、数据处理和控制器设计由MATLAB/Simulink 完成，调试由ControlDesk 实现。

将dSPACE 半实物仿真平台和稳瞄伺服控制系统相结合，可以非常快速地实现系统建模和控制器设计［1］。

1.2 频率特性拟合方法

本文拟采用扫频法建立系统数学模型［2－5］。该方法首先给系统输入一个正弦扫频信号，并记录输出信号，得到系统各频率处的原始输入和输出，采用最小二乘法［1，7－8］，对输入的激励信号数据和记录的输出信号数据处理，消除噪声得到系统幅频和相频特性。

设系统输入、输出分别为

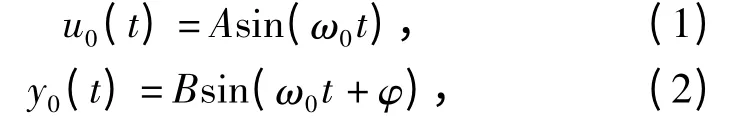
式中:A，B 分别为输入、输出信号的幅值;B/A 为系统传递函数的线性幅值;由于输入信号的相位为0，所以φ 既是输出信号的相位，也是系统传递函数的相位。

由dSPACE 获得某个频率下输出y0(t)的一组采样数据为y(kT)，根据三角公式可知

式中:Bs、Bc分别为正弦、余弦分量系数。当采样频率f0，测试频率点ω0，采样点数N 满足等式ω0=时，

因此系统输出y0(t)的线性幅值和相位差为

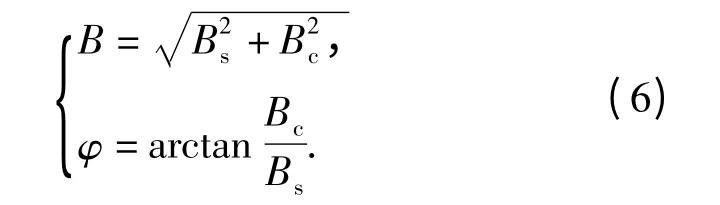
系统传递函数在测试频率点处的线性幅值B/A和相位φ 就可求得。

1.3 系统辨识的方法

图1为dSPACE 平台的系统辨识流程图。

首先对控制对象的模型阶次和转折频率进行估计，确定扫频范围，再利用dSPACE 平台给测试对象一个设定好的扫频信号源，并保存相关的扫频数据，根据最小二乘法处理保存的数据，得到系统的频率特性数据(线性幅值，相位和频率)，绘制出系统的线性幅频和相频曲线。

图1 系统辨识流程图Fig.1 Flowchart of system identification

将得到的系统频率特性数据导入MATLAB 中的Ident 系统辨识工具箱［6－7］，根据预估的系统阶次辨识出最优的数学模型，对该模型进行转化，最终导入Simulink，进行分析。需要说明的是Ident 的输入为所要辨识系统的线性幅值、相位和频率，而控制系统通常概念上Bode 图为对数幅频曲线，其之间差20 倍的LOG 关系，本文在辨识过程中的幅频曲线纵轴采用线性幅值，其单位为无量纲的增益，在控制器设计过程中的幅频曲线纵轴采用对数幅值，其单位为dB.

2 仿真实验

为了验证本方法的正确性，在MATLAB 中对一个已知的二阶系统进行仿真实验。给定扫频信号幅值为1，频率变化范围为1～100 Hz，采样频率为5 kHz.将仿真得到的大量数据导入最小二乘拟合算法，获得该对象的频率特性数据，绘制出的线性频率特性如图2所示。

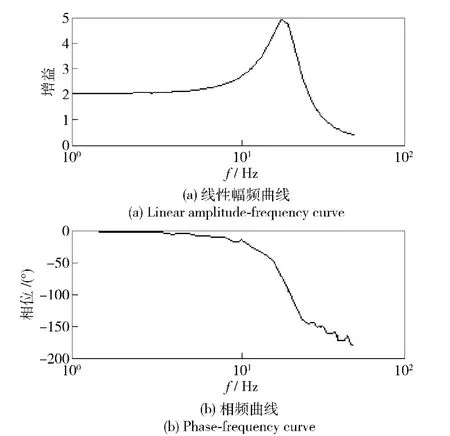
图2 二阶系统线性频率特性Fig.2 Linear frequency characteristic of object

将频率特性数据导入MATLAB 中的Ident 系统辨识工具箱，选择线性参数模型后，给定阶次为二阶，辨识出的模型和已知的二阶系统频率特性对比如图3所示。拟合度为95.2%，拟合精度较高，获得的模型传递函数为

对比可知，辨识结果较为精确，该辨识方法可行。

3 某稳瞄方位轴稳定回路实验

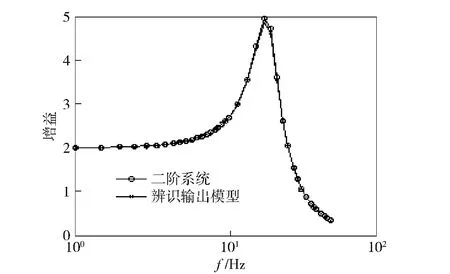
图3 二阶系统与辨识输出模型线性频率特性对比Fig.3 Comparison of linear frequency characteristics of object and model

选定的辨识对象为某型稳瞄系统速率稳定回路，如图4所示［8］。它由陀螺测量视轴相对惯性空间的速度，与速度命令形成误差信号，经过稳定回路控制器形成控制电压，通过伺服驱动器控制力矩电机，力矩电机产生驱动力矩，带动平台反向转动，消除误差。

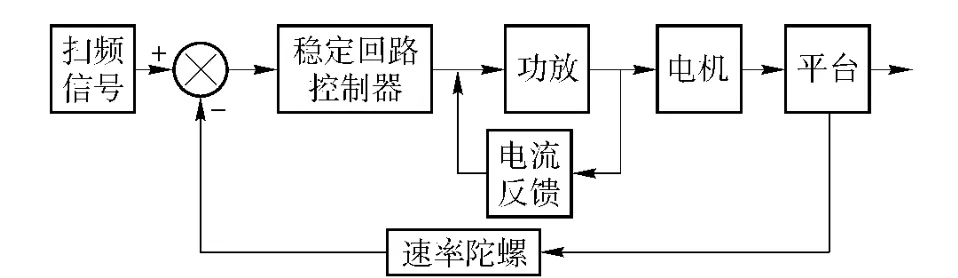
图4 稳瞄系统速率稳定回路Fig.4 Stabilizing loop of system

3.1 对象模型阶次和转折频率估计

对象模型阶次和转折频率是采用系统辨识方法对控制对象建模的一个重要参数。为了便于预估环路参数，辨识开始前，选择稳定回路控制器为比例控制，电流环带宽通常大于1 kHz，远远大于稳定回路转折频率，因而可以将其近似成一个比例环节［9］。从图4可知，辨识数据来源于控制系统的给定，因此可以将闭环系统看做反馈通道为单位负反馈，前向通道依次为控制器和功放、电机、平台以及陀螺的串联，因而从扫频给定到速率反馈整个前向通道阶次为一个四阶系统，综合考虑到谐振、摩擦和线扰等因素影响，实际系统应该是一个高阶系统，反馈通道为单位负反馈。

扫频频率区间应覆盖系统所有转折频率点，并向高频和低频有所延伸，速率稳定回路转折频率通常为30 Hz 左右，所以辨识扫频信号的合理区间为0.5～200 Hz.

已知稳瞄系统速率稳定回路控制器Gk(s)为比例控制;驱动器、电机、平台和陀螺的串联传递函数为Gp(s);整个速率稳定回路闭环传递函数为Gs(s).

因此

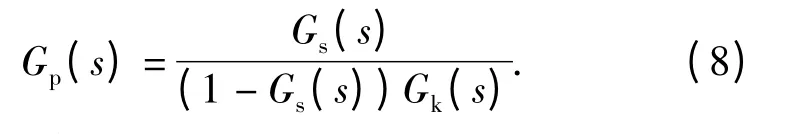
3.2 根据频率特性辨识系统模型

扫频信号作为速率稳定回路的给定，反馈信号为速率陀螺的信号。将给定信号、反馈信号和扫频信号的频率同时保存作为辨识的数据来源。频率区间选择0.5～200 Hz，采用与仿真实验同样的拟合算法，获得速率稳定回路频率特性如图5所示。

图5 稳定回路线性频率特性Fig.5 Linear frequency characteristic of stabilizing loop

输入系统频率特性数据，取模型为六阶系统，辨识输出模型频率特性和系统频率特性如图6所示，低频误差小于5%.

辨识获得速率稳定回路闭环传递函数为

图6 稳定回路与辨识输出模型线性频率特性对比图Fig.6 Comparison of linear frequency characteristics of stabilizing loop and model

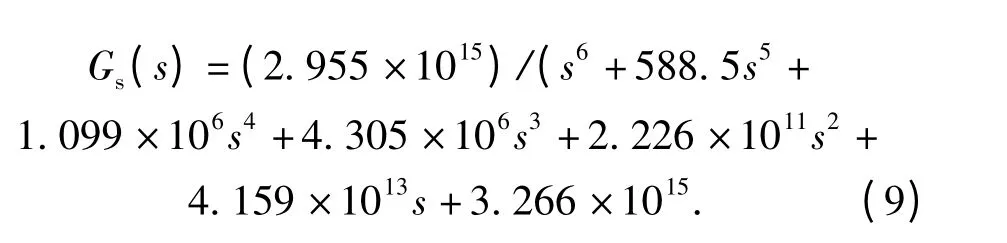
采用(8)式，得前向通道传递函数

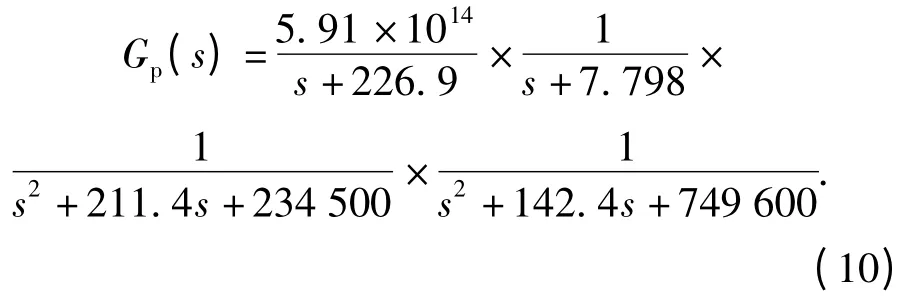
由以上分析可知，该传递函数是功放、电机、平台、陀螺和扰动等的串联组合，可以作为稳定回路的控制对象。

3.3 SISO 控制器设计

将(10)式导入SISO 控制系统设计工具箱，利用经典控制理论中典型的串联补偿方法设计获得的控制器为

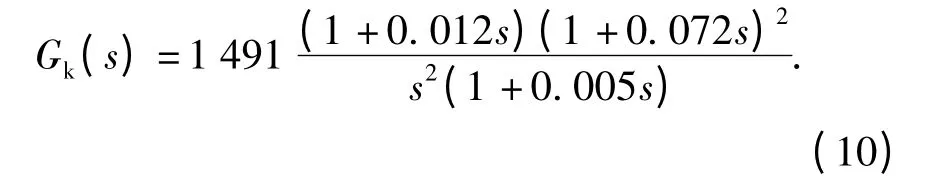
(10)式包含3 个0 点，其中2 个0 点重合，包含1 个极点和2 个积分环节。获得期望特性的频率曲线，如图7所示。

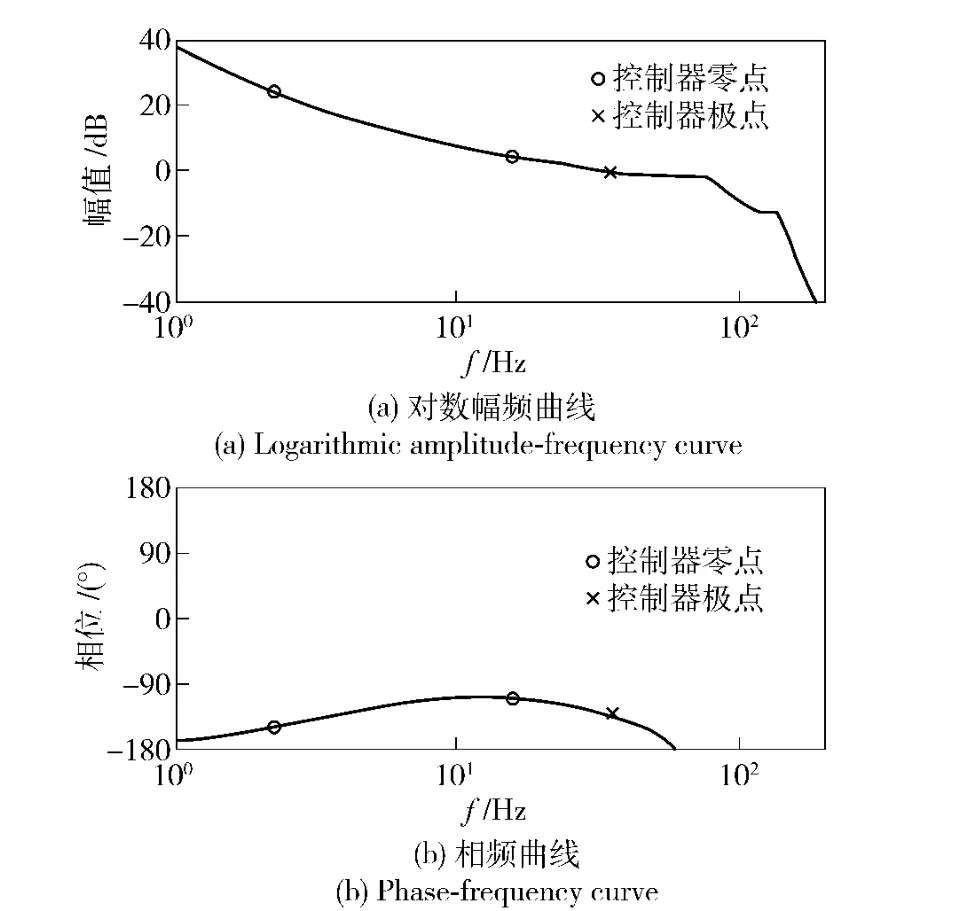
图7 SISO 工具箱开环Bode 图Fig.7 Open loop Bode diagram of SISO toolbox

将所设计控制器加入该半实物仿真实验平台运行，实测该控制器用于真实系统后的Bode 图如图8所示，由图7和图8可知，仿真开环剪切频率为31.5 Hz，实测为32 Hz，仿真相位裕度为50°，实测为53°，仿真结果和实测结果非常接近。

图8 实测开环Bode 图Fig.8 Bode diagram in actual test

4 结论

利用最小二乘法和系统辨识方法，在dSPACE半实物仿真平台上实现了陀螺稳定回路模型的建立，并基于该模型设计了控制器，仿真结果和半实物平台实验结果非常接近，证明了这种方法的有效性和实用性。由辨识过程可知，辨识数据是在稳瞄系统实际工况下扫频获得的，其中包含了摩擦和线扰等非线性因素，因而这种建模方法获得的模型更接近实际。最终获得的稳定回路模型可以直接作为位置回路的控制对象，为位置随动控制器和瞄准线跟踪控制器的设计提供了依据。本方法实现了速率稳定回路的数字控制，其控制器可以直接移植到嵌入式处理器进行实时控制而无需调试，极大地提高了效率。本方法为数字化机载光电稳瞄伺服控制系统分析和设计奠定了基础。

References)

［1］ 潘峰，薛定宇，徐心和.基于dSPACE 半实物仿真技术的伺服控制研究与应用［J］.系统仿真学报，2004，16(5):936－939.PAN Feng，XUE Ding－yu，XU Xing－he.The research and application of dSPACE based hardware－in－the－loop simulation technique in servo control［J］.Journal of System Simulation，2004，16(5):936－939.(in Chinese)

［2］ 李言俊.系统辨识理论及应用［M］.北京:国防工业出版社，2006.LI Yan－jun.Theory and application of system identification［M］.Beijing:National Defense Industrial Press，2006.(in Chinese)

［3］ 范世珣，范大鹏，张智永，等.机电装置频率特性的数字化测试方法研究［J］.动力学与控制学报，2007，5(1):92－96.FAN Shi－xun，FAN Da－peng，ZHANG Zhi－yong，et al.The research on the digital measurement of frequency response characteristics of machatronics equipment［J］.Journal of Dynamics and Control，2007，27(6):92－96.(in Chinese)

［4］ 刘德朋，赵叶华.关于频率特性的一种精确测量算法［J］.电子测量与仪器学报，2006，20(3):54－56.LIU De－peng，ZHAO Ye－hua.A novel precision measuring algorithms of frequency characteristic［J］.Journal of Electronic Measurement and Instrument，2006，20(3):54－56.(in Chinese)

［5］ 张绍宁，陈鹏.非标准设备频率特性的自动化测试［J］.战术导弹技术，2006，(6):76－79.ZHANG Shao－ning，CHENG Peng.Automation test for frequency characteristic of nonstandard facilities［J］.Tactical Missile Technology November，2006，(6):76－79.(in Chinese)

［6］ 薛定宇，陈阳泉.基于MATLAB/Simulink 的系统仿真技术与应用［M］.北京:清华大学出版社，2006.XUE Ding－yu，CHENG Yang－quan.system simulation technology and application based on MATLAB/Simulink［M］.Beijing:Tsinghua University Press，2006.(in Chinese)

［7］ Lennart Ljung.System Identification Toolbox 7 User’s Guide［EB/OL］.［2008－10］.http:∥www.mathworks.cn/help/ toolbox/ident/ug/ug_intropage.html.

［8］ 张璟玥，纪明，王惠林.机载稳瞄控制系统模型及仿真分析［J］.应用光学，2006，27(6):491－496.ZHANG Jing－yue，JI Ming，WANG Hui－lin.Modeling and simulation of airborne stabilized sighting system［J］.Journal of Applied Optics，2006，27(6):491－496.(in Chinese)

［9］ 秦继荣，沈安俊.现代直流伺服控制技术及其系统设计［M］.北京:机械工业出版社，1999.QING Ji－rong，SHENG An－jun.DC servo control of modern technology and system design［M］.Beijing:China Machinery Press，1999.(in Chinese)