K-行正交矩阵的几点性质
贾书伟
(西华大学数学与计算机学院,四川成都610039)
正交矩阵作为一种特殊的矩阵,在整个矩阵理论体系中具有十分重要的作用,它的广泛应用推动了特殊类矩阵理论的深入研究.文献[1]讨论了正交矩阵的性质,文献[2]给出了次正交矩阵的概念,并研究了次正交矩阵的性质,文献[3]将次正交矩阵的概念加以推广,给出了亚次正交矩阵的概念,文献[4]和[5]给出了广义次对称(反次对称)矩阵和广义次正交矩阵的概念,并讨论了它们的性质及它们之间的关系,文献[6]研究了K-拟次正交矩阵的性质,文献[7]给出了右转置矩阵、左转置矩阵和全转置矩阵与正交矩阵的充分必要条件及一些相关结果.近年来,一些矩阵论工作者对矩阵引入了行转置矩阵概念[8],并研究它的一些性质[9],进而又有矩阵论工作者讨论了矩阵的行正定性[10]问题,但还未发现有矩阵论工作者讨论行正交性问题.因此,在此基础上,本文引进行(列)对称矩阵、行正交矩阵以及行对合矩阵的概念,通过研究,得出了一些有用结果.
为方便讨论,规定A-1、A*、AT、|A|分别为矩阵A的逆矩阵、伴随矩阵、转置矩阵和行列式,R表示实数域集合,Rm×n表示m×n实矩阵,E表示n阶单位矩阵,Jn=J表示次对角线上元素全为1,其余元素全为0的n阶方阵,“A⇒B”表示由A可以推出B.
1 定义和引理
定义1[8]设A=(aij)∈Rm×n,则矩阵A的行转置矩阵与列转置矩阵,并记为AR与AC.
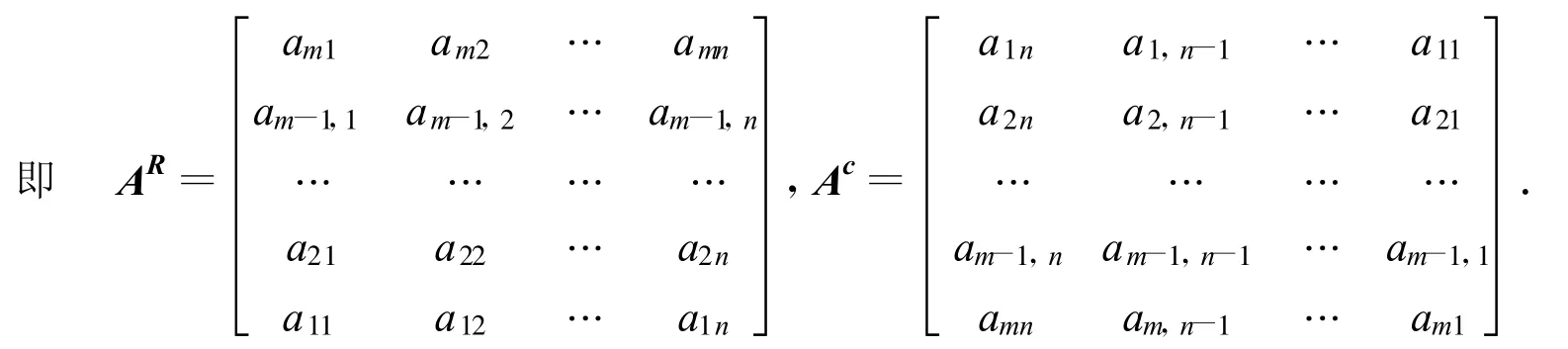
若AR=A(AC=A),则A称为行(列)对称矩阵;若AR=-A(AC=-A),则A称为行(列)反对称矩阵;若AR=AC,则A称为行列对称矩阵.
由定义不难得到:J-1=JT=J,JR=Jc=J2=E.
引理1[9]设A,B∈Rm×n,则有下列结论:
⑴AR=JmA,AC=AJn;
⑵(AR)R=A,(AC)C=A;
⑶(kA)R=kAR,(kA)C=kAC(k∈R);
⑷(AR)T=(AT)C,(AC)T=(AT)R
⑸(A±B)R=AR±BR,(A±B)C=Ac±Bc;
⑹设B∈Rn×k,则(AB)R=ARB,(AB)C=ABC.
引理2[11]A=(aij)∈Rn×n,且A为可逆矩阵,则A*=|A|A-1.
引理3 设A∈Rn×n,且A可逆,则(A-1)R=(AC)-1,(A-1)C=(AR)-1.
证明 因为A∈Rn×n且可逆,所以(A-1A)R=(A-1)RA=ER=J,于是A-1R=JA-1=(AJ)-1=(AC)-1.同理可证(A-1)C=(AR)-1.
定义2 设A∈Rn×n,若ARA=AAR=KJ(其中0≠K∈R),则A称为K-行正交矩阵.
特别地,若K=1,则A称为行正交矩阵;若K=-1,则A称为行反正交矩阵.
定义3 对于任意实矩阵A,若(AR)2=KJ,则称A为K-行对合矩阵.当K=1时,称A为行对合矩阵;当K=-1时,称A为行反对合矩阵.
2 主要结果
定理1 如果A∈Rn×n为K-行正交矩阵(0≠K∈R),那么A、AR、AC都是可逆矩阵.
证明 当A为K-行正交矩阵时,则有ARA=AAR=KJ,(0≠K∈R),等式两端同取行列式得:|JAA|=|AJA|=|KJ|⇒|J||A|2=Kn|J|,又因J为可逆矩阵,从而|A|2=Kn≠0,所以|A|≠0,故A为可逆矩阵;因J为可逆矩阵,故|J|≠0,所以|AR|=|JA|=|J||A|=|AJ|=|AC|,即|AR|=|AC|=|J||A|≠0,故AR,AC也是可逆矩阵.
定理2 如果A为K-行正交矩阵,那么J与A、AR、AC、A*、A-1、AT可交换.
证明 因A是行正交矩阵,从而ARA=AAR=KJ,结合引理1得JAA=AJA=KJ,又因为A可逆矩阵,等式两端右乘A-1得:JA=AJ,所以AR=AC;(即A是行列对称矩阵);JAR=JJA=A,ARJ=JAJ=AJJ=A,即JAR=ARJ;同理:J与AC可交换;JA*=J|A|A-1=|A|(AJ)-1=|A|(AC)-1,A*J=|A|A-1J=|A|(JA)-1=|A|(AR)-1=|A|(AC)-1,所以,(A*J=JA*;JA)-1=(AJ)-1=(AC)-1,A-1J=(JA)-1=(AR)-1,又因AR=AC,所以JA-1=A-1J;JAT=(AJ)T=(AC)T,ATJ=(JA)T=(AR)T,又因AR=AC,所以JAT=ATJ.
定理3 如果A∈Rn×n为K-行正交矩阵(0≠K∈R),那么
⑴(AR)T=(AT)R,(AC)T=(AT)C;
⑵(AR)-1=(A-1)R,(AC)-1=(A-1)C.
证明 由定理2知AR=AC,再由引理1得:(AT)R=(AC)T=(AR)T,所以(AR)T=(AT)R,类似的,可以证明(AC)T=(AT)C;
⑶由AR=AC和引理3可知:(A-1)R=(AC)-1=(AR)-1,即(AR)-1=(A-1)R类似的方法可以证明:(AC)-1=(A-1)C.
定理4 若A是行对称且K-行对合矩阵,则A是K-行正交矩阵.
证明 因为A是行对称且K-行对合矩阵,有AR=A,(AR)2=KJ,所以,AAR=ARA=(AR)2=KJ,则A是K-行正交矩阵.
推论1①若A是行对称且行对合矩阵,则A是行正交矩阵;
②若A是行对称且行反对合矩阵,则A是行反正交矩阵.
定理5 若A是行对称且K-行正交矩阵,则A是K-行对合矩阵.
证明 因为A是行对称且K-行正交矩阵,有AR=A,AAR=ARA=KJ,所以,(AR)2=ARA=KJ,则A是K-行对合矩阵.
推论2①若A是行对称且行正交矩阵,则A是行对合矩阵;
②若A是行对称且行反正交矩阵,则A是行反对合矩阵.
定理6 若A是K-行对合且K-行正交矩阵,则A是行对称矩阵.
证明 因为A是K-行对合且K-行正交矩阵,有(AR)2=KJ,AAR=ARA=KJ,所以,AAR=ARAR,从而AR=A,则A是行对称矩阵.
推论3①若A是行对合对称且行正交矩阵,则A是行对称矩阵;
②若A是行反对合且行反正交矩阵,则A是行对称矩阵.
[1] 刘志明.关于正交矩阵性质的讨论[J].重庆师范学院学报:自然科学版,2000,17(s):162-164.
[2] 刘丽萍.次正交矩阵及其性质[J].山西财经大学学报,2000,22(s):205-206.
[3] 陈琳.亚次正交矩阵及性质[J].周口师范学院学报,2004,21(5):28-30.
[4] 郭伟.广义次对称矩阵及广义次正交矩阵[J].西南师范大学学报:自然科学版,2000,25(1):18-22.
[5] 戴立辉,王泽文,刘龙章.正交矩阵的若干性质[J].华东地质学院学报,2002,25(13):267-267.
[6] 刘玉,蔡乌芳.K-次正交矩阵及其性质[J].南通大学学报:自然科学版,2009,8(1):72-75.
[7] 许永平,石小平.正交矩阵的充要条件与O正交矩阵的性质[J].南京林业大学学报:自然科学版,2005,29(2):54-56.
[8] 袁晖坪.行(列)对称矩阵的Schur分解和正规阵分解[J].山东大学学报:理科版,2007,42(10):123-126.
[9] 袁晖坪.行(列)对称矩阵的奇异值分解[J].中北大学学报:自然科学版,2009,30(2):100-104.
[10] 何承源,淑恒.实矩阵的行正定性[J].西华大学学报:自然科学版,2010,29(5):49-50.
[11] 黄正达,李方等.高等代数(上册)[M].杭州:浙江大学出版社,2008.

