基于零点采样的电力系统频率算法分析与仿真

徐伊岑

（无锡商业职业技术学院，江苏无锡 214153）

基于零点采样的电力系统频率算法分析与仿真

徐伊岑

（无锡商业职业技术学院，江苏无锡 214153）

针对基于特征点采样的频率算法的问题，采用线性插值的方法对已有的经典过零点测量法进行了改进，而实际情况中电压信号里掺杂着的些许高次谐波和噪声干扰在建模时也加以了考虑，最后利用MATLAB对上述算法在频率相对固定的条件下进行了仿真，证明了算法的有效性。

频率;测量算法;零点;MATLAB

频率是电力系统的一个重要参数，准确地获取电力系统运行中的频率以作为实施安全稳定控制的重要状态反馈量，对于监测负荷的用电安全性及其动态地调整电厂输出功率以及对电力系统以外的其他领域都具有极其重要的意义。

1 频率测量方法现状

目前国内外常用的频率测量方法有很多，［1－3］主要有三种类。①解析法。［4，5］该方法对信号观测模型进行数学变换，将待测量表示为样本值的显函数来估计，其特点是算法简明，计算量不大，但是在涉及复杂的数学推导时，为简化分析和计算，只能采用简单的信号模型。难以考虑谐波、非周期分量和噪声影响，而且还受到过零点的影响，虽然有学者提出了改进的方法，但都没有从源头上抑制它的误差，而只是相对减小它的误差。②DFT（FFT）类算法及其改进算法。［6，7］傅氏滤波的测频算法具有较强的滤波能力，它的基本思路是来自傅里叶级数，它不仅能完全滤掉各种整数次谐波和纯直流分量，对非整次高频分量和按指数衰减的非周期分量包含的低频分量也有一定的抑制能力。但是傅里叶算法数据窗长较长为一个周波，且对于衰减的非周期分量滤波效果有时达不到要求，在最严重的情况下，计算误差可能超过10%，而且必须是同步采样，否者也会有采样误差。③周期法及其改进算法。［8，9］该类方法具有计算简单、跟踪速度快、精度高等优点，虽然为了达到预期的测量精度的要求需要增加采样周期数，但如今DSP的速度已足够满足采样数据的处理，使得此类方法具备了光明的应用前景。

周期法频率测量有两种基本思路：峰值（谷值）法和零点法。峰值（谷值）法是利用数据相互比较来找出采集的数据相邻两个周期的两个最大（最小）值，并且记住这两个数据在数组中的位置，也就是它的时刻，进而计算出频率，而零点法则利用两个过零点数据来计算频率。这两种方法基本思路大同小异，只是处理的特征点不同。传统的零点法都是以标准正弦波作为测量模型的，但是实际情况中往往在电压信号中还掺杂着些许高次谐波、噪声干扰等，本文将针对该问题对零点法进行改进，并通过算例仿真验证改进算法的正确性。

2 过零点检测法分析

一般测量电力系统的频率都是利用单相电压的波形来分析，电力系统正常运行时，系统频率为工频（50Hz）。对于f的估计，可以直接通过对电压信号的采样值进行一些简单的处理来求得。电压为纯正弦量时，即：

图1 u（t）的波形图

u（t）的采样值为u（k），k=1、2、3、4、．．．，实际中是不可能出现采样点刚好就都是过零点的情况，因此只能通过处理采样的数据来间接获得过零点的时刻。通过比较前后两个采样点的电压值来判断是否有零点出现，即如果它们符号相反，就说明它们之间存在一个过零点，而如果它们的符号相同就说明它们之间不存在零点。

设u（m－1）、u（m）分别为一个周期中的两个采样点，则有：

先判断是否有采样点u（m）、u（m－1）刚好为零，若有则它就是零点时刻，若没有就是

则它们的符号相反，那么在这两点之间肯定有一个零点。

由于按照上面的方法这样比较后，虽然能够确定在这两点之间肯定有零点出现，但仍然得不到具体的过零点时刻，传统的算法一般采用线性插值法来估计出过零点的时刻。也就是假设采样率足够大，使得这两点之间的极小的范围内，电压波形是线性的。设采样间隔△t，采样点m－1处的电压值为u（m－1），m处的电压值为u（m），就可以求出m－1、m点之间的零点时刻的近似值t1＇。

由式（5）、（6）求出t1、t3后，代入式（2）后即可求得从t1到t3这一时段内的平均系统频率f1。同样，也可以由第二类过零点，根据式（2）来计算出频率，具体与第一类过零点的求法相同可求出f2。

LED灯具有快速切换、易调制、成本低和体积小的优点,本文在发射端处利用LED灯发出高频率、高强度的调制光载波信号,在水中信道传输,在接收端处利用光敏电阻等光电器件接收可见光的载波信号,解调后获得光传输的信息。

由t2、t4来计算这两个频率f1、f2都是近似值，与标准值都存在一定的误差，那么根据相关理论，如果求它们的平均值来代替它们中的任何一个，误差可能就会更小。

式中，f为这个周期内的平均频率。

3 对频率测量方法的改进

在前面所讲的基于特征点的频率测量算法是以标准正弦波作为测量模型的，但在实际情况中往往在电压信号中还掺杂着些许高次谐波、噪声干扰等，考虑到有谐波和噪声干扰的存在，前面的电气信号观测模型相应的也要改变，要加入一些谐波和噪声干扰。

式中，n为谐波次数，Un为n次谐波幅值，φn为n次谐波初相位，ω1为基波角频率，ε（t）为随机噪声干扰。

一般情况下，低通滤波器都会滤掉电压信号中的7次及其以上谐波，剩下了2、3、4、5、6次谐波。根据电力系统实际运行经验，电网中的4、6次谐波一般含量很低，可以不用考虑，故只考虑2、3、5次谐波的干扰，其中3次谐波所占比例较大，需重点考虑。同样，在一般情况下，信号的信噪比都很高，但是在要求高精度的场合，我们还是要考虑噪声的影响。而噪声的产生和特性都比较复杂，不利于我们计算，在这里就将噪声简化为比较特殊的高斯白噪声（功率谱不变、服从高斯分布的噪声）。

传统的滤波方法虽然很简单、方便，但是根据实际运行中的经验，还是存在有待改进的地方，不仅滤波器会设计得很复杂，而且效果也不好，很难兼顾到所有谐波，并且噪声是一种随机信号，噪声干扰的模型很难固定。为此本文将利用自适应滤波器来消除这些杂波，系统的流程图如图2所示。

图2 滤波系统流程图

经过采样得到的数据u（n）之中含有很多的谐波和噪声干扰。假设输入信号为：

式中，T为输入信号的周期，N为一个周期内的采样个数，ε＇（n）为噪声干扰。

在理想情况下，陷波器的输出量h（n）应该为：

这样便可得到需要的正弦波，也就是原信号的基波分量。

采用二阶直接形式的自适应IIR陷波滤波器，其传递函数H（z）具有镜像对称形式：

式中，z为复数变量，β是一个接近1但略小于1的常数。

引入β能够保证H（z）的每一个零点附近都有一个极点与之对应，而且零点与极点在相同的半径上，但是极点稍靠近原点。当z离开零点时，从它到零点的距离与从它到极点的距离几乎相同，即保证了（在陷波频率外的其它频率处）：

在零点时，传递函数的幅值肯定为零，而在其他的点，由于β无限接近1，使得零点与极点很接近，那么在其它的点幅值就近似为1，从而确保陷波器在陷波频率外的其它频率处不会衰减。β的大小也决定了陷波频率的宽度，β越大，陷波频率的宽度越窄;反之，β越小，陷波频率越宽。而在理论上，β越大，陷波器的精度就越高，但是当频率变化很快的时候，可能无法跟踪频率，从而造成大的误差，因此，β值应该根据具体的情况选用。

二阶直接形式的自适应IIR陷波滤波器一个明显的优点就在于，在3dB衰减的陷波带宽BW和陷波频率参数α可以单独调节，也就是说，不需将带宽BW或β固定，即可获得稳定的自适应IIR滤波器。通过调节陷波频率参数α，则可以跟踪信号频率的变化来自适应的改变陷波器性能。

由式（12）可知，数字陷波滤波器的零点为：

当z1=ejωT或者z2=ejωT时，H（ejωT）=0，此时的频率就是陷波频率。假设采样时间间隔为Ts，则对应的实部可以由余弦求出：

设Ts=10－3s，根据要求，陷波频率f应该就是电压信号基波频率50Hz，则有：

为了实现它的滤波器功能，得出它的算法，用偏移方差σ来检验它的滤波性能。可以由式（19）求出它的逆Z变换，得出输入与输出数列之间的关系。

先让H（z）除以z，然后展开得：

通过与几种常见的Z变换比较，最终可以求出：

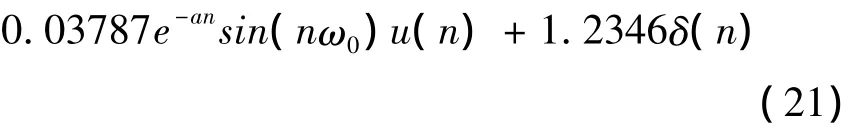
式中a=－0．2346，ω0=18，u（n）为单位阶跃响应。

4 算例仿真与分析

选用MATLAB作为频率算法的仿真软件，借助其强大的绘图功能，可以由MATLAB直观输出仿真波形，验证出算法的性能。

假设电压信号为：

式中f0为标准频率50Hz。

仿真时加入10%的2次谐波、20%的3次谐波、10%的5次谐波，采样频率取为5KHz，一个周期内采样100个点，共采样100个周期，则得到的采样电压为：

对应的波形如图3如示。

图4给出了滤波处理后得到的最终频率测量结果。可以看出，测量的频率基本上是正确的，只是在第一点不完全等于50Hz，因此该算法要在第二周期以后就可以准确测量任意初相角的正弦电压波形的频率。

图3 含有谐波的电压波形图

图4 含有谐波时零点法测量的频率

5 结论

本文在研究经典过零点检测法的基础上，把零点分为两类（波形上升时的过零点、波形下降时的过零点），计算出各自的频率，求出平均值，得到测量的频率，并采用线性插值法对零点法的进行了分析。在考虑谐波、噪声时分别对算法进行了仿真分析，验证了算法的可行性。仿真结果表明，在频率相对稳定时该算法基本可行，且测量原理简单、计算量小、测量精度较高。

［1］卞星明，文远方，雷琴．电力系统测频算法比较［J］．高电压技术，2006，32（5）：111－114．

［2］欧立权．电力系统频率测量方法及应用的研究［D］．长沙：湖南大学，2007．

［3］练锴，冯振明，陆明泉．过零点检测法改进［J］．电子测量技术，2006，29（1）：39－40．

［4］应展烽，吴军基，易文俊．基于小波变换和三点法的极薄频率测量［J］．电机与控制学报，2010，14（2）：65－70．

［5］AGHAZADEH R，LESANIH，SANAYE－PASAND Metal．New technique for frequency and amplitude estimation of power system signals［J］．IEE Proc．Gener．Transm．Distrib，2005，152（3）：435－440．

［6］李玲，金国彬，谢卫才．电力系统基波频率的高精度测量新方法［J］．湖南工程学院学报，2009，19（2）：5－7．

［7］J．Szafran，W．Rebizant．Power system frequency estimation［J］．IEE Proceedings，1998，145（5）：578－582．

［8］Nguyen C T，Srinivasan K．A New Technique for Rapid Tracking of Frequency Deviations Based on Level－Crossing［J］．IEEE Trans on PAS，1984，103（8）．

［9］Begovic MM，Djuric P M，Phadke A G．Frequency Tracking in Power Networks in the Presence of Harmonics［J］．IEEE Trans on PWRD，1993，8（2）．

［编校：邓桂萍］

The Analysis and Simulation of Power System Frequency Algorithm Based on Zero Point Samp ling

XU Yicen
（Wuxi Institute of Commerce，Wuxi Jiangsu 214153）

Aiming at the problem of frequency measurement algorithms based on feature points sampling，the classic zero－crossing point measurement was improved by using linear interpolation method．When the mathematicalmodel was built，the harmonic components and random noise mixed with the voltage signal in the actual situation were considered．Finally，simulations were given，which proves the effectiveness of the algorithm．

frequency;measurement algorithm;zero point;MATLAB

TM743

A

1671－9654（2011）04－051－04

2011－10－14

徐伊岑（1982－），女，湖南长沙人，讲师，工学硕士，研究方向为机电一体化与自动控制。