卷积型Calderón-Zygmund算子的数值算法

段 汕，牛小娇，杨占英

(中南民族大学数学与统计学学院，武汉430074)

1 研究背景

根据 Beylkin-Coifman-Rokhlin(B-C-R) 算法［1］，算子可以用合适的小波基进行刻画性分析，这样给算子的数值计算带来极大的方便，如计算奇异积分算子.

设T是D→D'的一个连续线性算子，存在一个联系于T的分布核K(x，y)∈D'(Rn×Rn)对所有支集不交的f，g∈D(Rn)，有:

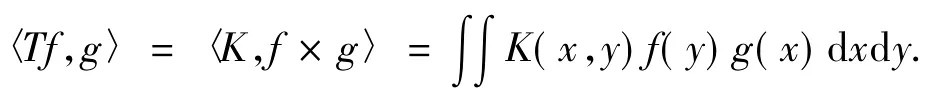
我们称K∈D'(Rn×Rn)为标准核［2］，若它在Ω=(Rn×Rn){x=y}上满足:

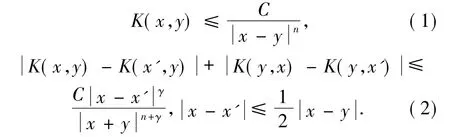
其中0＜γ≤1，C表示一个与所考虑的变量无关的常数，不同位置处的取值可以是不同的.此时记K∈SK(γ).如果T可延拓为L2(Rn)上的有界算子，则T被称为Calderón-Zygmund算子(C-Z算子)，记为T∈CZO(γ).

文［3］中的T1定理表明，在(1)和(2)式下，T可延拓为L2(Rn)上的有界算子当且仅当T满足T1条件:

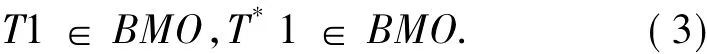
和弱有界条件:

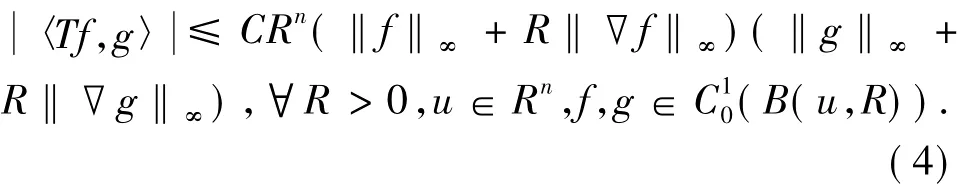
而在工程应用中，更多的会碰到卷积型算子，如Hilbert算子和Riesz算子.对于卷积型算子T，其分布核K(x，y) 可被写作K(x，y)=k(x－y)，即:

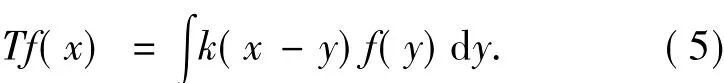
对任意的R＞0，记则T∈CZO(γ)意味着T满足以下条件:

(i)消去条件: 对任意的 ΨR(x)∈(B(0，1))，

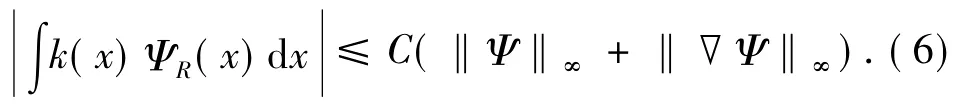
(ii)大小条件:

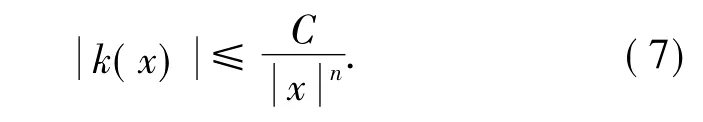
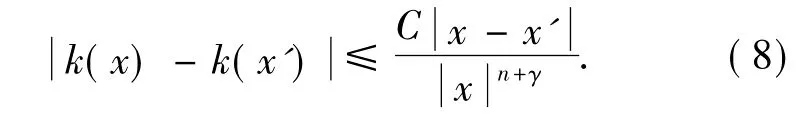
一个卷积型算子T∈CZO(γ)也被写作T∈CCZO(γ)或记作k(x)∈Kγ.

对卷积型算子的逼近问题，文［4］曾提出一种基于n维小波的分析方法.记B(x，R)是中心在x，半径为R的球，记En={0，1}n{0}，对任意的ε=(ε1，ε2，…，εn) ∈En，记 Φε(x) ∈C20(B(0，2M)) 为Daubechies小波(M为一确定的常数).记Λn={λ=(ε，j，k)，ε∈En，j∈Z，k∈Zn}，对任意的j，k，记，那么是的一组规范正交基.实际上，对于λ∈Λn，记，在分布的意义下有:

文［4］引入下面的环状算子，对任意的R≥0，ε∈En，定义(x) 如下:

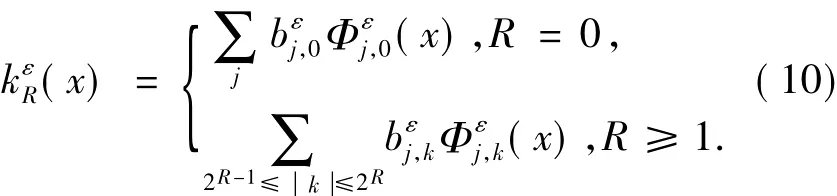
记表示对应于(x) 的环状算子，记TR=用带状算子TR逼近T，得到定理1.

定理1假设1≤p，q≤∞，0＜γ≤1和R≥1.对卷积型C-Z算子T，下式成立:

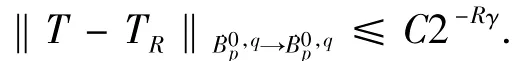
这里，采用算子的基于n维小波的数值算法，结合Besov空间的小波刻画得到算子在Besov空间上的逼近算法，从而

推广了定理1的结论，得到下述定理2.

定理2设，若则:

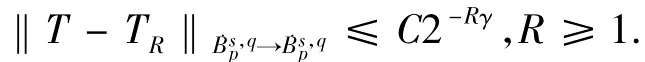
2 准备知识

首先描述一些函数空间的准备知识.

用S和S'分别表示由急减光滑函数组成的Schwarz空间和由缓增广义函数组成的空间.S'/P表示模去全体多项式，选取φ(x)∈S，使得supp⊆，并且当时，记.对，通常的Besov空间可定义如下:

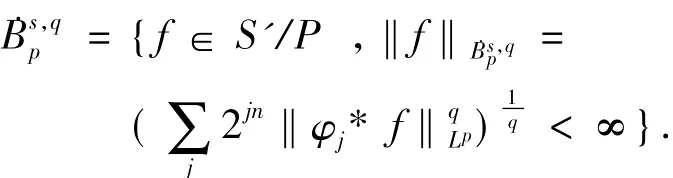
根据文献［5］中的结果，Besov空间中的函数也可采用相应的小波系数作刻画性描述.

引理1对任意的f∈S'/P，若我们能够定义则在分布的意义下有设我们有:

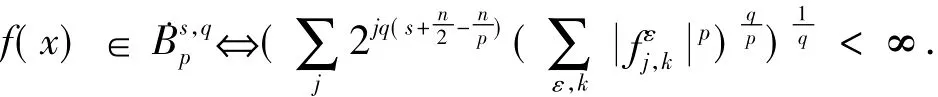
其次，描述在定理2的证明过程中需要的分布核的Daubechies小波系数估计.

对于分布核k(x)∈Kγ，在(9)式成立的前提下，有下述引理 2 成立［4］.

引理2给定0＜γ≤1，若k(x)∈Kγ，则有:

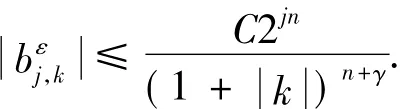
最后，介绍一类非卷积型算子，它的分布核为Daubechies小波和它的卷积的特定和.

假设Φε(x) 和 Φε'(x)是充分光滑的Daubechies小波，对于若m≥ 0，记若m＜0，则.由Φε(x) 的性质，很容易得到函数的性质［4］.

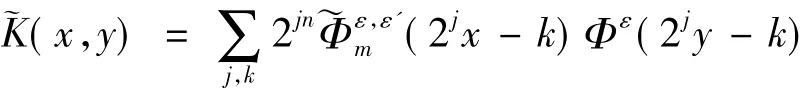
的一类非卷积型算子.

引理 3［4］对，算子满足(1)，(2)，(3) 式和如下条件:

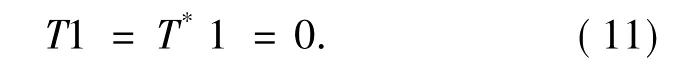
此外，在定理2的证明中，还需要用到下面的引理4，其证明可查阅文献［6］.

引理4设0＜γ≤1，0≤s＜γ，1≤p，q≤∞，若T满足(1)，(2)，(3)式和条件(11)，则T在˙Bs，qp上连续.

3 定理2的证明

为证明定理2，我们首先对(10)式定义的分布核所对应的环状算子TεR的范数进行估计，见定理3.

定理3设1和 ε ∈En.若T∈CCZO(γ)，则:

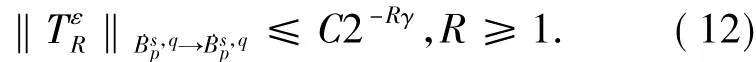
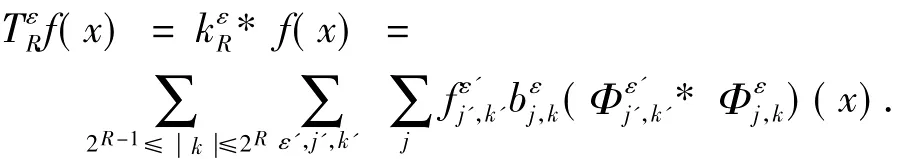
令j'=j+m，则有:

因此，

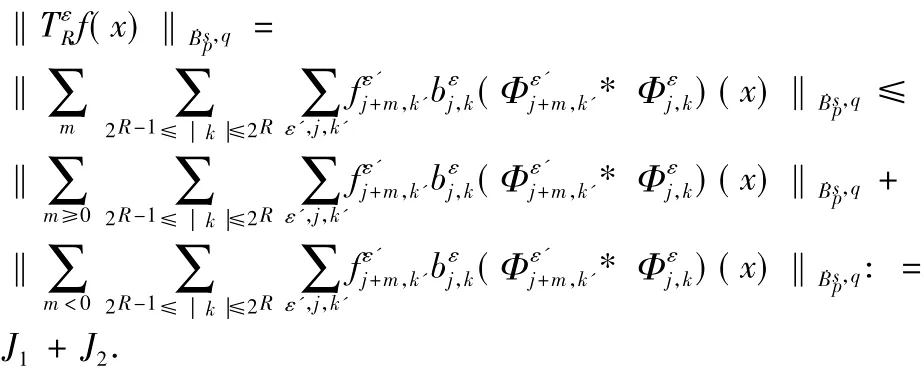
接下来，我们先对J1进行估计.

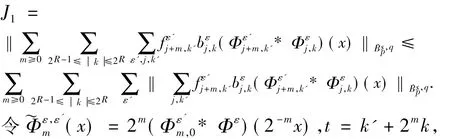
结合函数的卷积运算，可得:

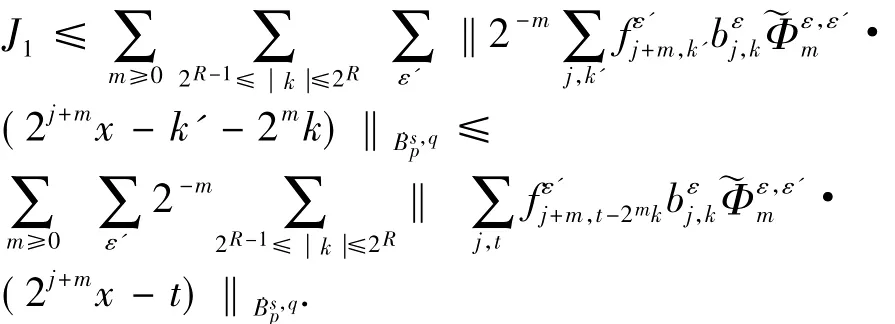
注意当 ε，ε'∈En，且若记则根据引理3和引理4，对应于分布核的算子在Besov空间上连续，因此:

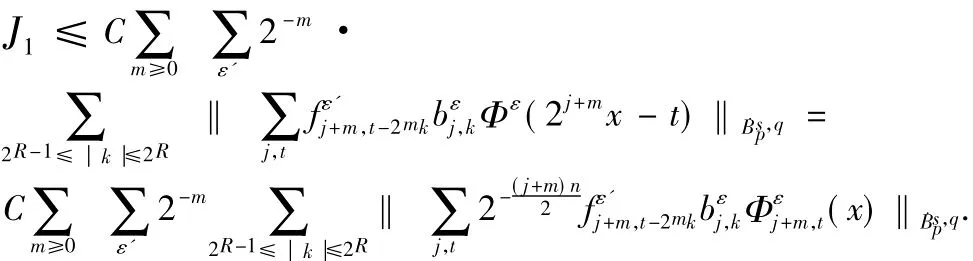
运用引理1，Besov空间上的函数可以用小波系数来刻画，所以有:

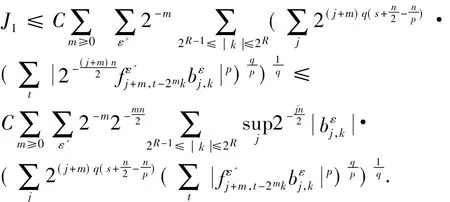
从而可得到:

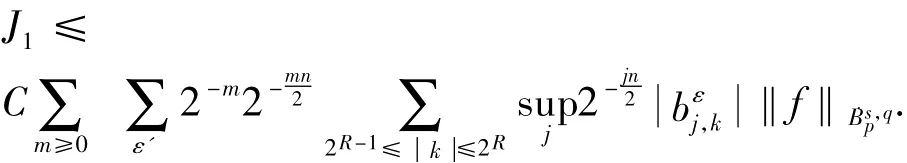
接下来，运用引理2中的估计，有:

综合J1和J2的估计结果，即可得到(12)式.

下面，我们来完成定理2的证明.运用定理3，我们有:

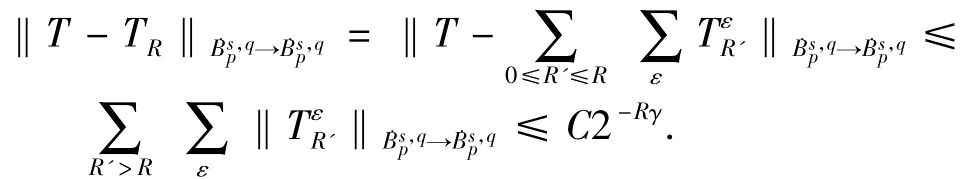
至此，定理2证毕.

［1］Beylkin G，Coifman R，Rokhlin V.Fast wavelet transforms and numerical algorithms I［J］.Comm Pure Appl Math，1991，46:141-183.

［2］程民德，邓东皋，龙瑞麟.实分析［M］.2版.北京:高等教育出版社，2008:309-315.

［3］David G，Journe JL.A boundedness criterion for generalized Calderón-Zygmund operators［J］.Ann of Math，1984，120(2):171-197.

［4］杨占英，杨奇祥.卷积型 Calderón-Zygmund算子的新算法［J］.数学学报，2008，51(6):1061-1072.

［5］杨奇祥.小波与分布:小波应用的部分机理［M］.北京:科学技术出版社，2002:67-82.

［6］LemariéP G.Continuitésur les espaces de Besov des opérateurs détinis par des integrals singulières［J］.Ann Inst Fpuier(Grenoble)，1985，35(4):175-187.