接触界面压力对高次谐波和键合强度的影响

李战慧，吴运新，隆志力

(1. 中南大学 机电工程学院，湖南 长沙，410083；2. 长沙理工大学 汽车与机械工程学院，湖南 长沙，410076)

接触界面压力对高次谐波和键合强度的影响

李战慧1,2，吴运新1，隆志力1

(1. 中南大学 机电工程学院，湖南 长沙，410083；2. 长沙理工大学 汽车与机械工程学院，湖南 长沙，410076)

为减少超声键合换能器劈刀在振动过程中的非线性振动，改善劈刀振动的稳定性，提高芯片键合的强度，建立超声波在接触界面传播的模型。在超声引线键合机上，通过改变劈刀和变幅杆接触界面的接触压力，分别测量变幅杆和劈刀的振动和芯片键合强度，并对劈刀振动位移进行频谱分析。研究结果表明：超声波通过接触界面时，由于接触界面层的非线性特性会产生高次谐波和波形畸变；劈刀振动中的高次谐波成分对芯片键合强度造成负面影响。只有当接触界面压力适中时，劈刀振动的波形畸变最小，高次谐波成分最少，超声波的非线性系数最小，芯片键合强度最大。测量劈刀振动的高次谐波可以作为预测芯片键合程度的一种方法。

接触界面；谐波；换能系统；非线性

如果超声波的幅度足够小，并且在同一均质材料中传播，超声波的非线性成分较小可以忽略，超声波的幅度将保持不变。如果超声波在非线性材料中传播，那么超声波的非线性成分不能忽略，非线性成分会导致超声波幅度和频率发生变化。国内外研究者对超声波在固体接触界面的非线性效应研究主要集中在：超声波通过接触界面后对物体的影响[1−2]，通过测量超声波透过接触界面后透射波的强度和产生的高次谐波来预测接触界面的黏接强度[3−7]，接触界面粗糙度与超声波透射波关系[8]等方面。在超声换能器的研究中，人们研究了劈刀和变幅杆拧紧螺钉拧紧力矩变化对换能器的谐振频率和阻抗[9]的影响以及对劈刀振动模态、振动节点位置变化[10−13]和键合强度[14]的影响。以上研究均是从实验角度出发得出的结论，没有从理论上解释拧紧力矩变化对键合强度产生影响的原因。为此，本文作者建立超声波在接触界面传播的模型，运用数学方法进行求解，计算结果在超声引线键合换能器实验台上得到验证。

1 理论基础

2个物体通过压力p0接触到一起。由于材料表面都有一定的粗糙度，所以，物体表面接触只是通过几个粗糙峰连接。设有一列超声纵波在物体1中沿X轴传播，垂直射到2个物体的接触表面。由于超声波和接触表面之间相互作用，所以，在物体1中产生反射波，在物体2中产生透射波。在粗糙峰接触处，超声波发生反射和透射，而在空隙处由于空气和材料之间声阻抗的差异较大，只发生反射(图1(a))。

随着外界压力p0的变化，物体之间粗糙峰发生变形，接触面积会发生变化，超声波在接触界面的反射和透射系数也会发生变化。由于材料表面粗糙峰分布的随机性，物体之间的准确接触面积很难计算。

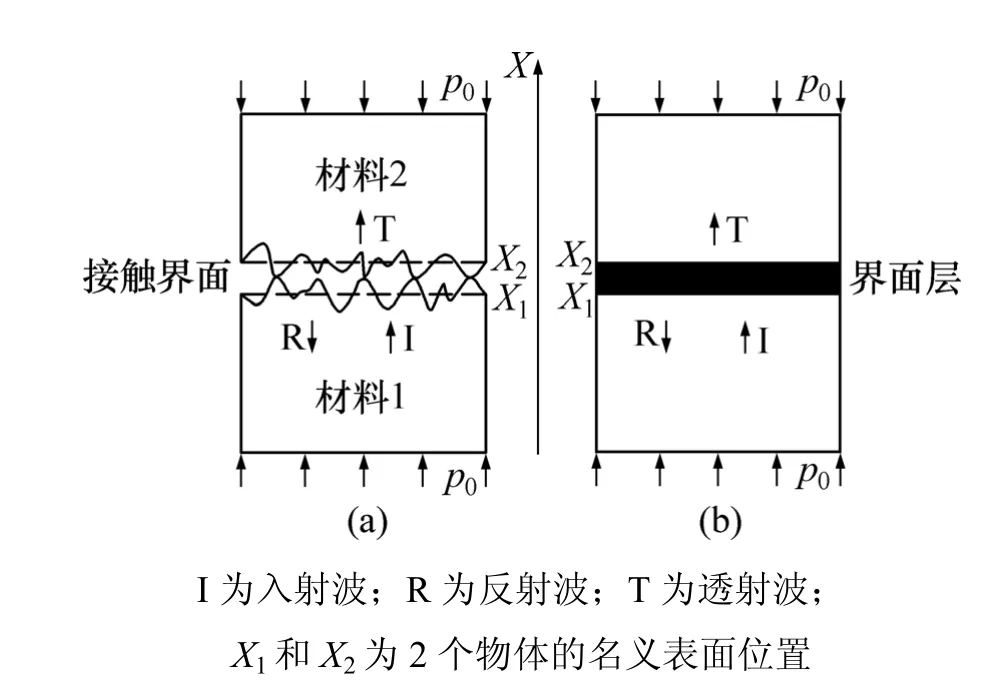
图1 超声波在接触界面传播Fig.1 Ultrasonic propagation at contact interface

为了简化超声波通过接触界面的描述，将物体的接触界面(X1和X2之间部分)看成一个界面层(图1(b))。界面层是一个非线性层，其力学特性随着接触压力的变化而发生变化，在外力作用下界面层的应力和应变表示为二阶分量的形式：

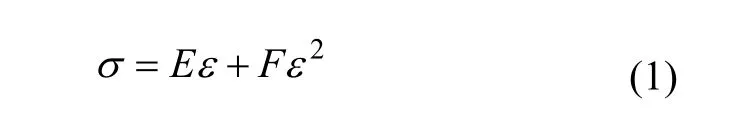
式中：σ为应力；ε为应变；E和F分别为界面层一阶和二阶弹性模量。定义非线性系数为：

当接触界面压力较小时，由于2个物体之间只通过几个粗糙峰接触在一起，增加很小的压力会造成接触界面应力增加，所以，这时接触界面层的非线性系数很大；随着接触压力的增大，接触面积逐渐增大，非线性系数逐渐减小；当压力增大到一定程度后，由于材料发生塑性变形，非线性系数增大。

当超声波通过接触界面层时，超声波的运动方程为：

ρ为接触界面层材料的平均密度。

方程(3)的准确解析解不容易得到，在局部范围内运用文献[15]中的近似解析方法求解。

设方程(3)的初始条件为：

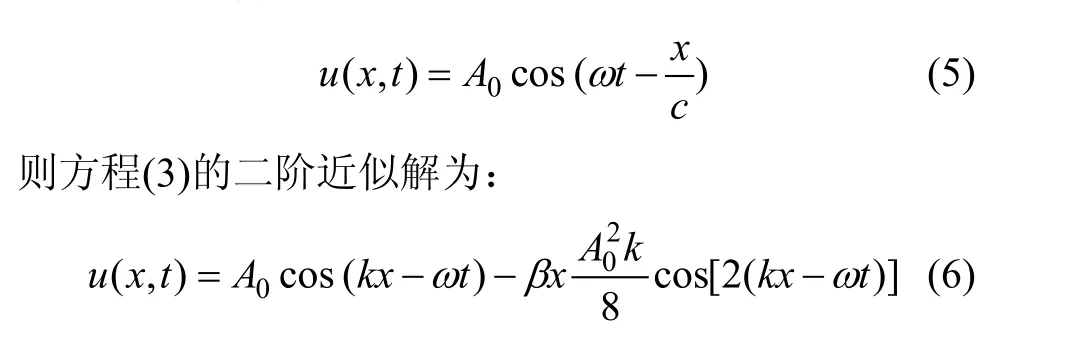
其中：k为超声波的波数。

在方程(6)的右边，第1部分为基波，第2部分为二次谐波。二次谐波的幅度与接触界面层的非线性系数、传播距离和波数成正比。

设A1和A2分别为基波和二次谐波的幅度，则

通过分别测量基波的振动幅度和二次谐波的振动幅度A2可以计算得到非线性系数。

2 试验与结果

2.1 试验

试验在60 kHz热超声引线键合机上进行。热超声引线键合换能器系统主要由超声发生器、PZT(压电陶瓷)、变幅杆、劈刀和安装环等组成(如图2所示)。由超声波发生器产生频率的高频(约为60 kHz)交流电压信号施加到PZT压电陶瓷片上，利用逆压电效应，转换为振幅为几十nm的沿轴向超声压缩纵波，超声波经过变幅杆的聚焦和放大作用后，在变幅杆的末端，振动幅度达到几 μm，经过变幅杆和劈刀之间的接触界面后，在劈刀中转换为横波。金球在劈刀的带动下相对于芯片做平行于芯片的振动，破除芯片表面的氧化层实现金属原子之间的接触，在压力和温度作用下，实现键合。

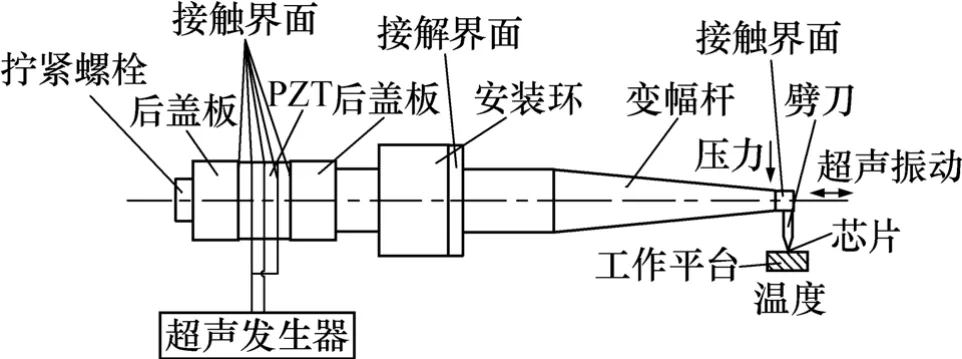
图2 超声换能系统结构Fig.2 Structure of ultrasonic transducer system

超声波在超声键合换能系统中的作用是破除芯片表面的氧化层以及激活金属的位错能。超声波在换能系统中传播要经过多个接触界面(如图 2所示)。由于接触界面是在螺栓预紧力的作用下接触到一起的，预紧力变化导致接触界面层的特性参数发生变化，透射超声波发生变化，从而影响芯片键合强度。

通过改变劈刀和变幅杆接触界面的接触压力，测量劈刀和变幅杆振动及其芯片键合强度变化的规律。试验中采用的参数如表1所示。

表1 试验键合参数Table 1 Bonding parameters of experiment

2.2 结果与讨论

用多普勒激光测振仪测量得到劈刀的振动波形，如图3所示。劈刀的振动波形不再是正弦曲线，在位移的峰值处出现了畸变。波形畸变主要是由于接触界面层的非线性特性产生的二次谐波。对试验采样的劈刀振动位移进行频谱分析，分析范围为0～200 kHz，结果如图4所示。

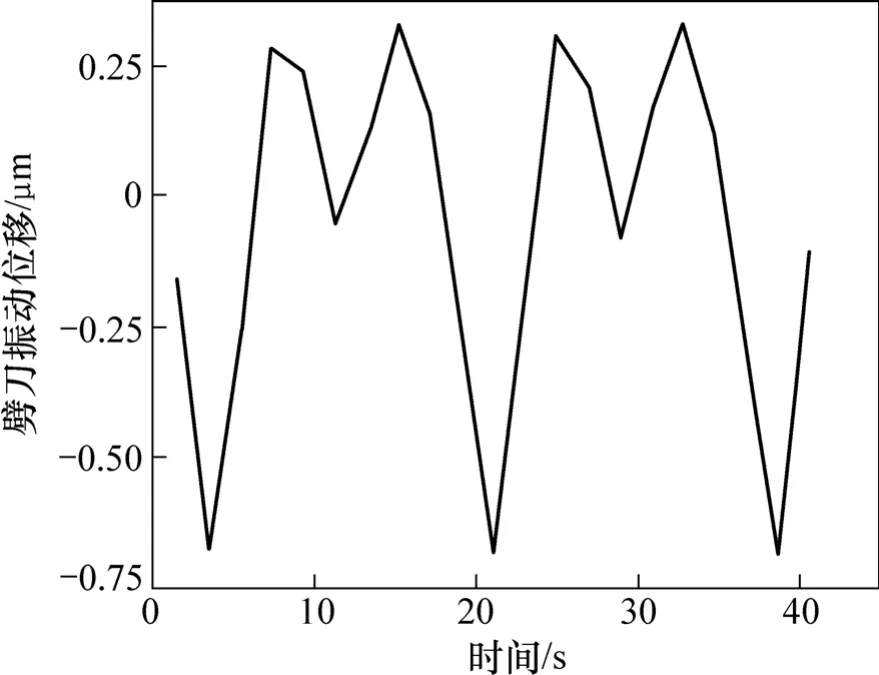
图3 振动位移波形畸变Fig.3 Vibration displacement wave form distortion

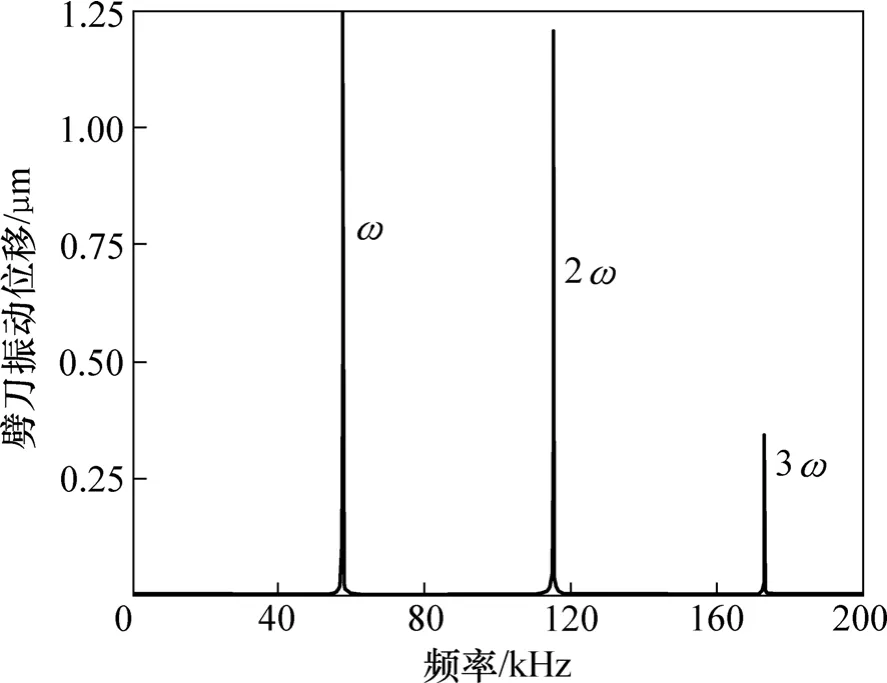
图4 劈刀振动的频谱Fig.4 Spectrum of capillary vibration displaument

由图4可以看出：在0～200 kHz内劈刀的振动中存在3种频率成分：ω，2ω和3ω，分别定义为基波、二次谐波和三次谐波。三次谐波幅度与二次谐波幅度相比，可以忽略。

分别测量在劈刀和变幅杆接触界面在不同接触压力下劈刀的振动位移，采用频谱分析得到基波和二次谐波的幅度，采用式(8)可计算出劈刀和变幅杆接触界面不同接触压力下的非线性系数，如图5所示。

由图5可见：当劈刀和变幅杆接触界面的压力较小时，超声波的非线性系数大于 1，这时由于接触界面之间的压力小，只有几个粗糙峰接触在一起，接触面积较小，非线性系数较大；随着界面之间接触压力的增大，接触面积增大，界面的变形减小，接触界面层的非线性系数减小；当接触界面的压力在6～10 kPa之间时，接触界面之间的接触面积不大，界面层的变形与压力成正比，二次弹性模量减小，所以，非线性系数最小；当接触压力大于10 kPa后，随着压力的增大，接触界面之间的材料进入塑性变形阶段，界面层的非线性系数又增大。

当非线性系数较小时，劈刀的振动中二阶以上谐波成分较少，劈刀的振动主要是工作频率的振动，有利于芯片氧化层的去除和金属位错能的激发和芯片的键合。

由图6可以看出：当劈刀和变幅杆接触界面接触压力较小时，芯片的键合强度较低，随着接触界面接触压力的升高，芯片键合强度升高；当接触界面接触压力 6～10 kPa之间时，芯片的键合强度没有明显变化；当接触界面之间的接触压力大于10 kPa后，芯片的键合强度随着接触界面压力的增大而减小。

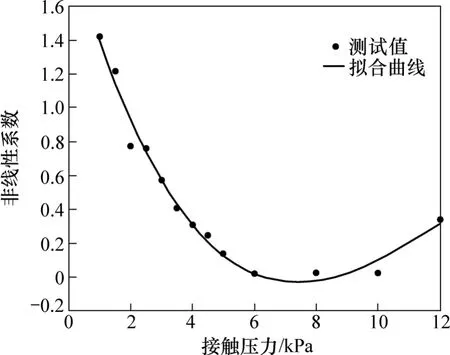
图5 非线性系数随着接触压力的变化Fig.5 Variation of nonlinear coefficient with pressure

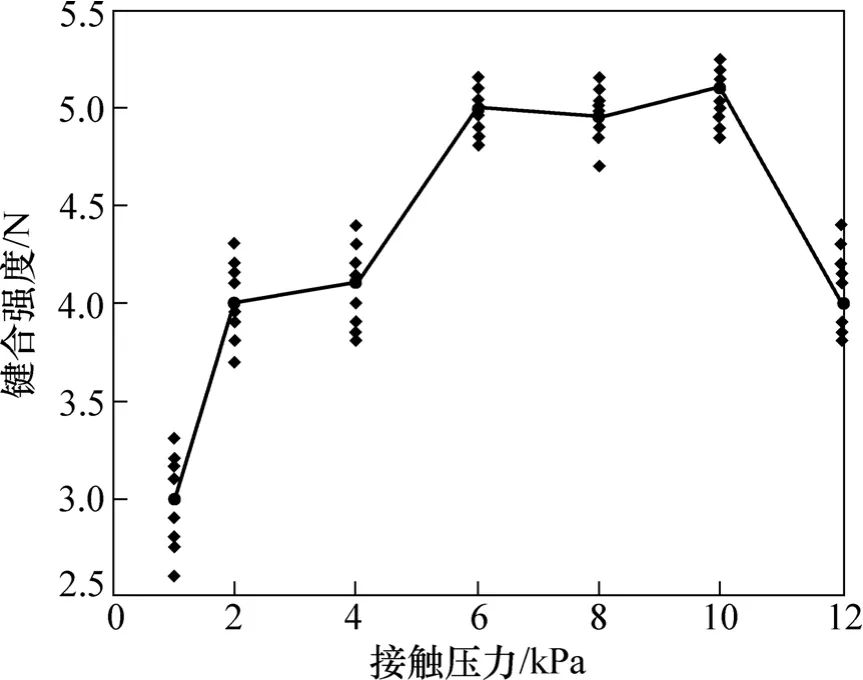
图6 键合强度与接触压力的关系Fig.6 Relationship between bond strength and pressure

3 结论

(1) 换能器接触界面的特性直接决定着超声波的传播效率、超声波波形畸变以及芯片键合的质量。

(2) 接触界面层的非线性系数随着接触压力的增大发生变化，粗糙峰发生变化，导致接触面积变化使其反射和透射波变化，从而影响劈刀的振动，影响芯片的键合强度。

(3) 当劈刀和变幅杆之间接触界面的接触压力较小时，随接触压力的增大，非线性系数减小，芯片键合强度增加；当劈刀和变幅杆之间接触界面之间的接触压力太大时，随接触压力的增大，非线性系数增大，芯片键合强度降低。

(4) 劈刀振动中多谐波成分对芯片键合强度有负面影响。高阶谐波成分的存在引起劈刀振动发生紊乱，直接影响芯片键合强度。为了提高芯片键合强度，应减小劈刀振动中的高次谐波成分。在生产过程中可以通过测量劈刀振动中的高次谐波成分来预测芯片键合强度。

[1]Qian J, Beskos D E. Harmonic wave response of two 3-D rigid surface foundations[J]. Soil Dynamics and Earthquake Engineering, 1996, 15: 95−110.

[2]Rogerson G A, Sandiford K J. Harmonic wave propagation along a non-principal direction in a pre-stressed elastic plate[J].International Journal of Engineering Science, 1999, 37:1663−1691.

[3]Barnard D J, Dace G E, Rehbein D K, et al. Acoustic harmonic generation at diffusion bonds[J]. Journal of Nondestructive Evaluation, 1997, 16(2): 77−89.

[4]Rothenfusser M, Mayr M, Baumann J. Acoustic nonlinearities in adhesive joints[J]. Ultrasonics, 2000, 38: 322−326.

[5]CHEN Jian-jun, ZHANG De, MAO Yi-wei, et al. Contact acoustic nonlinearity in a bonded solid-solid interface[J].Ultrasonics, 2006, 44: 1355−1358.

[6]Sweilam N H. Harmonic wave generation in nonlinear thermoelasticity by variational iteration method and Adomian’s method[J]. Journal of Computational and Applied Mathematics 2007, 207: 64−72.

[7]邓明晰. 复合结构界面粘接强度的声-超声评价研究[J]. 应用声学, 2005, 24 (9):292−299.

DENG Ming-xi. Nondestructive evaluation of adhesive strength of composite structures using an acoustic-ultrasonic approach[J].Applied Acoustics, 2005, 24(9):292−299.

[8]Pecorari C. Adhesion and nonlinear scattering by rough surfaces in contact: Beyond the phenomenology of the Preisach-Mayergoyz framework[J]. J Acoust Soc Am, 2004, 116(4):1938−1947.

[9]广明安, 韩磊, 李涵雄. 劈刀和肋环夹持工况对超声键合换能系统电学特性的影响[J]. 微细加工技术, 2006(10): 59−64.

GUANG Ming-an, HAN Lei, LI Han-xiong. Study of electrical characteristic of wire bonder transducer by clamp condition and on/off of bonding tool[J]. Microfabrication Technology,2006(10): 59−64.

[10]程宝, 韩雷. 超声键合装置中劈刀的稳态振型研究[J]. 振动与冲击, 2008, 27(2): 150−153.

CHENG Bao, HAN Lei. Model study on steady state vibration of bonding tool in ultrasonic bonding[J]. Journal of Vibration and Shock, 2008, 27(2): 150−153.

[11]程宝, 韩雷. 超声键合装置中劈刀稳态振动的试验建模[J].焊接学报, 2008, 29(2) :40−45.

CHENG Bao, HAN Lei. Experimental modeling on steady state vibration of bonding tool in ultrasonic bonding[J]. Transactions of the China Welding Institution, 2008, 29(2): 40−45.

[12]韩雷, 钟掘. 热超声倒装键合过程中的非线性动力学行为[J].半导体学报, 2006, 27(11): 2056−2063.

HAN Lei, ZHONG Jue. Nonlinear dynamical behaviors in flip-chip thermosonic bonding[J]. Chinese Journal of Semiconductors, 2006, 27(11): 2056−2063.

[13]HAN Lei, ZHONG Jue, GAO Gong-zhi. Effect of tightening torque on transducer dynamics and bond strength in wire bonding[J]. Sensors and Actuators A, 2008, 141: 695−702.

[14]隆志力, 韩雷, 吴运新, 等. 芯片键合换能系统中接触界面的影响分析[J]. 压电与声光, 2009, 30(8): 511−513.

LONG Zhi-li, HAN Lei, WU Yun-xin, et al. Effect of contact interface on transducer system on thermosonic bonding[J].Piezoelectrics & Acoustooptics, 2008, 30(8): 511−513.

[15]钱祖文. 非线性声学[M]. 北京: 科学出版社, 1992: 334−337.

QIAN Zu-wen. Nonlinear acoustic[J]. Beijing: Science Press,1992: 334−337.

(编辑 陈爱华)

Effect of contact interface pressure on higher order harmonic wave and bond strength

LI Zhan-hui1,2, WU Yun-xin1, LONG Zhi-li1

(1. School of Mechanical and Electronical Engineering, Central South University, Changsha 410083, China;2. Institute of Automobile and Mechanical Engineering,Changsha University of Science and Technology, Changsha 410076, China)

To reduce nonlinear vibration of capillary in ultrasonic transducer, improve vibration stability of capillary and increase bond strength, the model of ultrasonic propagation through contact interface was established. In ultrasonic wire bonder, the bond strength and velocity of horn and capillary was measured at different contact interface pressures between capillary and horn. The experiment results show that higher order harmonic wave and waveform distortion occur during the ultrasonic wave through a contact interface between two isotropic solids, which are pressed together higher harmonic wave components in capillary vibration have bad influence on bond strength, and only when contact interface pressure varies in a moderate range the largest bond strength can be reached. The measurement of higher order harmonic wave of capillary vibration is a effective method to forecast bond strength.

contact interface; harmonic wave; transducer system; nonlinearity

TN405.96

A

1672−7207(2011)02−0368−05

2009−11−07；

2010−03−20

高等学校博士学科点专项科研基金资助项目(20060533068)；国家自然科学基金资助项目(50605064)；湖南省科技计划项目(2007FJ3098)

吴运新(1963−)，男，广东兴宁人，教授，博士生导师，从事微电子封装和机械振动研究；电话：0731-88830813；E-mail：lzh-jdx@hotmail.com