Rank Distribution of A Class of Quadratic Form s

，

(1 School of Mathematics and Statistics，South-Central University for Nationalities，Wuhan 430074，China;2 Basic Course Department，Wuhan City Vocational College，Wuhan 430071，China)

1 Introduction

Throughout this paper，letq=pnfor an odd primepand a positive integern.F qdenotes the finite field withqelements.For an oddnandp=3，we study a class of highly nonlinear functionsQ(x)fromF3ntoF3

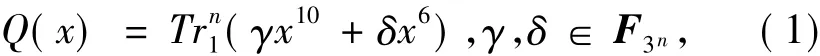
where(·)is the trace function fromF3ntoF3.These functions are quadratic ifγ≠ 0 orδ≠ 0.

The paper focuses on the rank distribution of the quadratic formsQ(x)，i.e.，the rank ofQ(x)and the times itoccurswhen(γ，δ)runs throughF3n×F3n{(0，0)}.The distribution is determined through finding the distribution of exponential sums whereTo achieve this goal，a linear code is introduced.The weight distribution of this code is completely determined，and the code is proved to be suitable to construct secret sharing schemes.

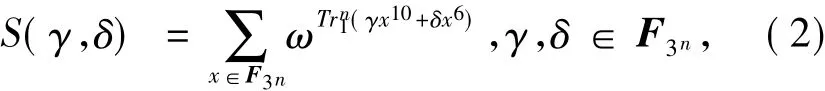
The remainder of this paper is organized as follows.Section 2 gives some definitions and preliminaries.Section 3 studies the rank distribution ofQ(x).Section 4 shows that the linear code obtained in thispaper is suitable for constructing secret sharing schemeswith interesting access structure.

2 Prelim inaries

The trace functionTrn1(·)fromF qtoF pis defined by Ref［1］

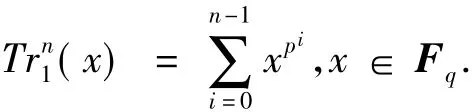
An［n，k;p］codeCis a linear subspace ofwith dimensionk.LetAidenote the number of codewords ofweightiin the codeC.The polynomialdenoted byWC(z)，is called the weight enumerator ofC.It is known in the theory of coding in Ref［2］that the dual codeC┴ofChas the weight enumerator as

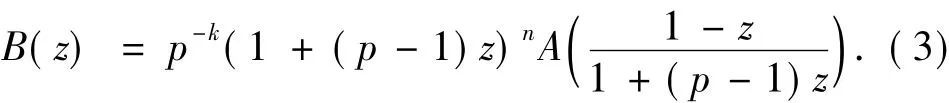
A functionf(x)onF qis a quadratic form if it can be written as a homogeneous polynomial of degree 2 onnamely of the formf(x1，…，xm)whereaij∈F p.The rankrof the quadratic formf(x)is defined as the codimension of theF p-vector space

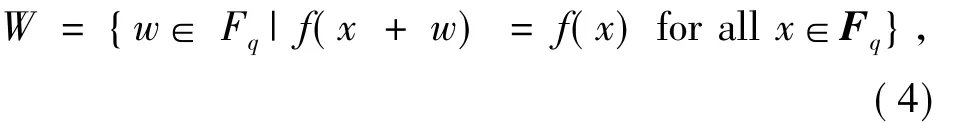
namely，|W|=pm－r.

The quadratic character ofF qis defined by

The quadratic form in odd characteristic has been well analyzed and the following lemma can be found in Ref［1］.

Lemma 1［1］Letfbe a nondegenerate quadratic form overF q，qodd，innindeterminates.Then for ρ∈F qthe number of solutions of the equationf(x1，…，xn) =ρis

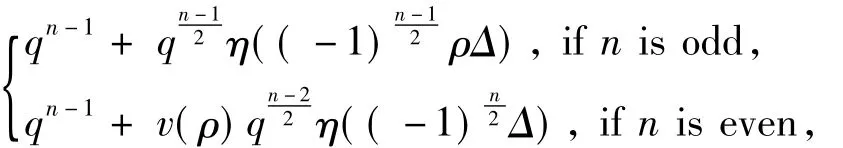
whereΔ= det(f)andv(x)is a functions inF qgiven by

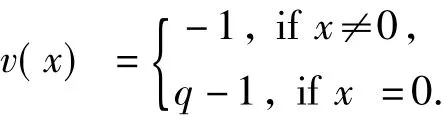
3 Rank distribution of Q(x)

In the sequel，the parameternis always assumed to be odd.The functionQ(x)defined by Eq.(1)is quadratic ifγ≠ 0 orδ≠ 0.In this case，its rank can be determined by as follows.

Proposition 1Forγ≠ 0 orδ≠ 0，the rank ofQ(x)is eithern，n－1，orn－2.

ProofLetρbe the rank ofQ(x).Then，3n－ρis the number of the variablez∈F3nsuch that

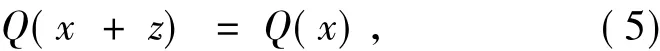
for allx∈F3n.Eq.(5)holds if and only if

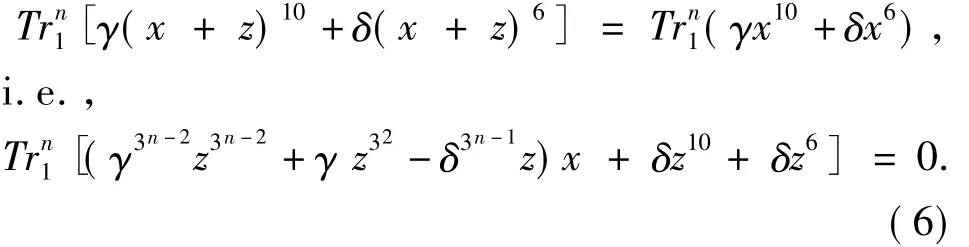
If Eq.(6)holds for allx∈F3n，then

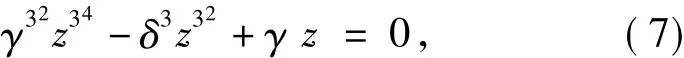
and

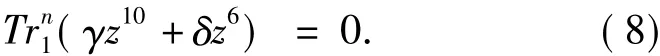
By Eq.(7)，we have

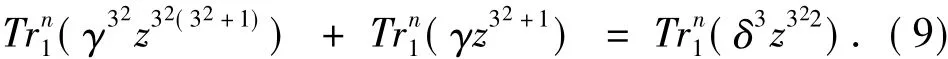
SinceTrn1(x3) =Trn1(x)，Eq.(9) can be simplified as

Thus，Eq.(7)implies Eq.(8)，and the number of solutionszto Eq.(5)is the same as that to Eq.(7).From the proof Lemma 2 in Ref［3］，Eq.(7)has one，three，or nine solutions inF3n.This implies the rank ofQ(x)is eithern，n－1，orn－2.

By Proposition 1，when(γ，δ)runs throughF3n×F3n{(0，0)}，Q(x)has rankn－i，i=0，1，2.Fori=0，1，2，letNidenote the number of(γ，δ) ∈F3n×F3n{(0，0)}such thatQ(x)has rankn－i.To determine the rank distribution ofQ(x)，i.e.，the values ofN0，N1，andN2，a linear code is introduced.

Definition 1For γ，δ∈F3n，letcγ，δbe the(3n－1)-dimensional vector indexed by the elements inas

Define a［3n－1，3n］linear code by

LetAjanddenote the number of vectors with weightjinCand its dual code，respectively．

Forj=1，3，the values ofcan be calculated as the following lemma．

Lemma 2

ProofThe case=0 can be easily proved，and we only give the proof for the case=0．If＞0，then there exist integers 0 ≤i1＜i2＜i3≤ 3n－2 and three elementsc1，c2，c3∈F3*such that

holds for all(γ，δ)∈F3n×F3n，where α is a primitive element ofF3n．This implies

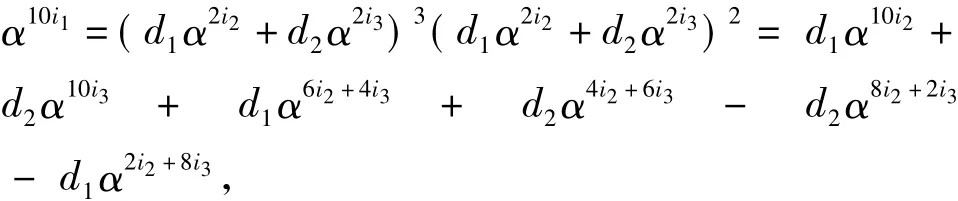
which implies

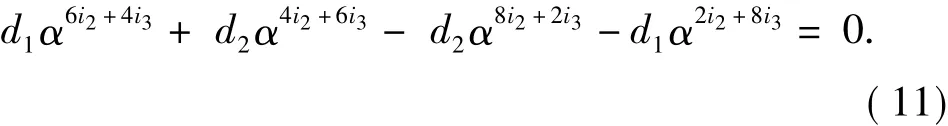
By dividingα2i2+2i3on both sides of Eq．(11)，we have

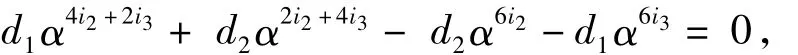
i．e．，

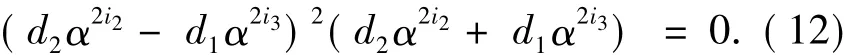
For an oddn，α2i2+ α2i3≠ 0 since －1 is not a square element inF3n．Thus，by Eq．(12)，we have

Plugging Eq．(13)into Eq．(10)，we have

Since 0≤i1＜i2＜i3≤ 3n－ 2，by Eq．(13)and(14)，we have

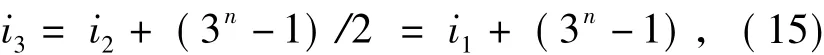
which is impossible．This proves

Applying Lemma 2，the weight distribution of the codeCcan be determined．

Theorem 1Theweight distribution ofCis given by

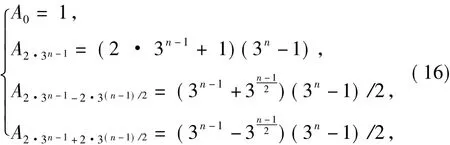
ProofLet HW(cγ，δ)denote theweightof codewordcγ，δ．Then，HW(c0，0)=0．

For fixedγ≠ 0，orδ≠ 0，Q(x)is a quadratic function overF3n．Let

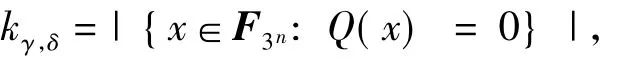
then HW(c) =3n－k．By Lemma 1，we have

γ，δγ，δHW(cγ，δ)take values in the set

For convenience，we setw0=0，w1=2 · 3n－1，w2=2 · 3n－1－2·，w3=2 · 3n－1+2 ·．The weight enumerator ofCis given by

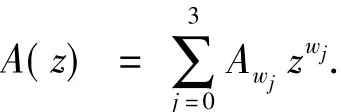
By Eq．(3)，the weight enumerator ofC⊥is given by

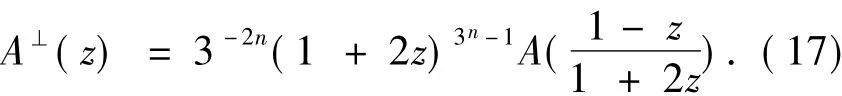
Note thatandare coefficients ofzandz3in Eq．(17)，respectively．

By expanding Eq．(17)and applying Lemma 2，we have

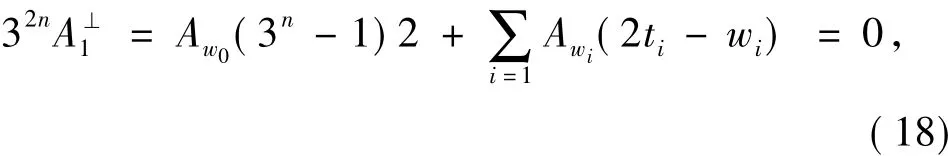
and

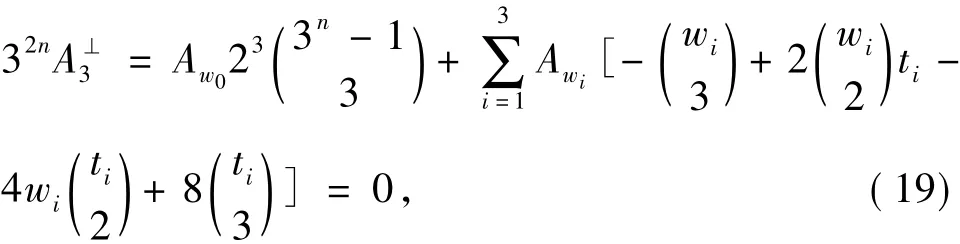
whereti=3n－1 －wi．

SinceAw0=1 andAw1+Aw2+Aw3=32n－1，by Eq．(18)and(19)，we have

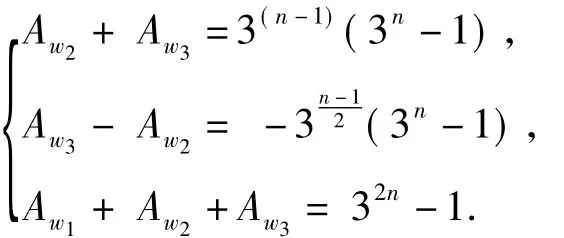
Eq．(16)follows system of equations above．

The exponential sumS(γ，δ)has the following properties．

Lemma 3For an oddn，we have

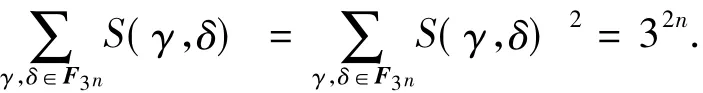
ProofIt is true that

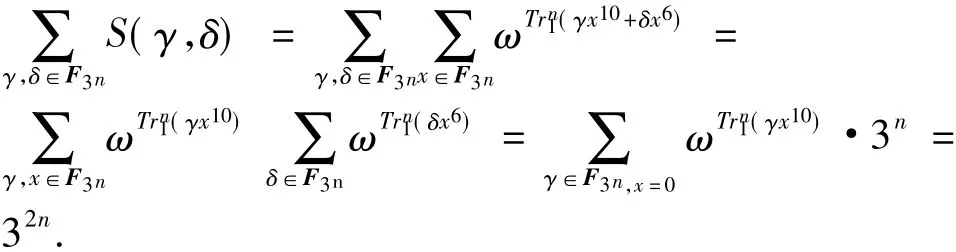
On the other hand，we have

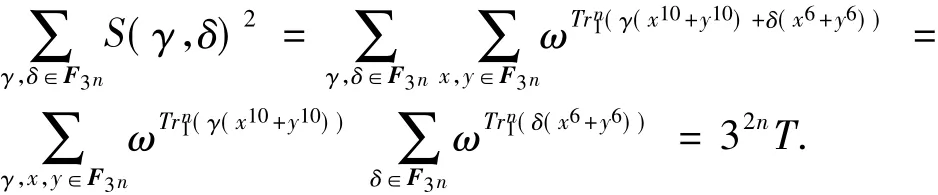
whereTis the number of solutions to

wherex，y∈F3n.The first equation in Eq.(20)is equivalent to

Ifxy≠ 0，then Eq.(21)is equivalent to

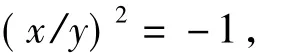
which contradicts to that－1 is not a square element ofF3nwherenis odd.Thus，Eq.(20)has the only solution(0，0)andT=1.

Theorem 2The values ofNifori=0，1，2 are given by

ProofBy Lemma 1，we have

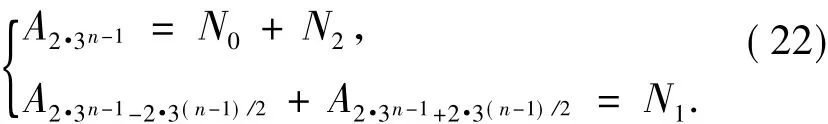
By Lemma 1 again，we have

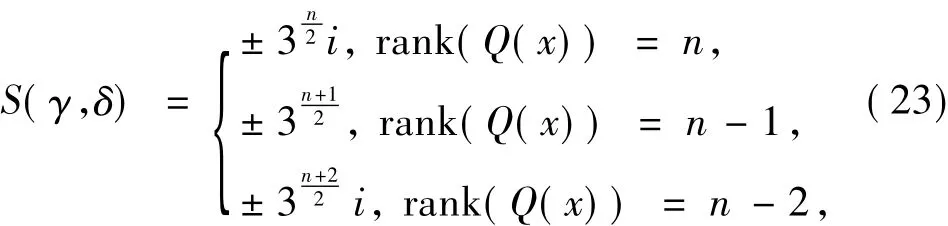
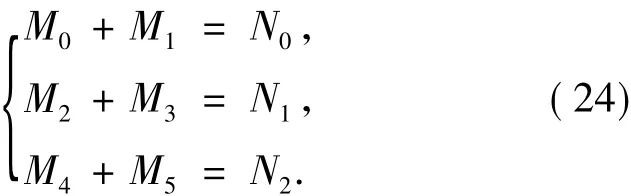
SinceS( －γ，－δ)is the complex conjugate ofS(γ，δ)，we have:

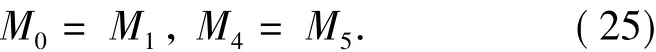
By Lemma 3，we have

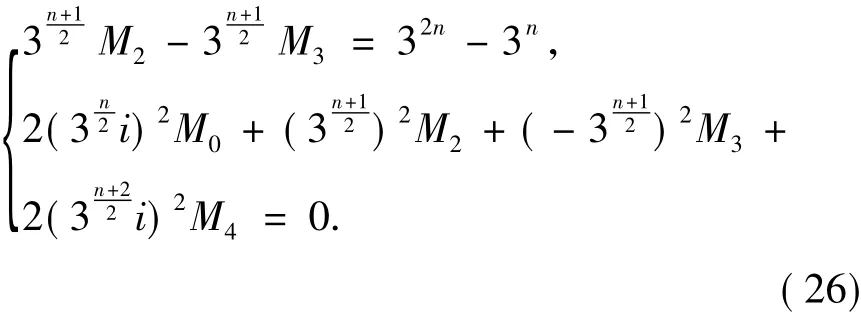
By Theorem 1 and Eq.(22) ～(26)，we have

The proof is finished.

From the proof of Theorem 2，the distribution of exponential sumS(γ，δ)can be obtained.

Corollary 1For an oddn，when(γ，δ)runs throughF3n×F3n {(0，0)}，the distribution ofS(γ，δ)is given by

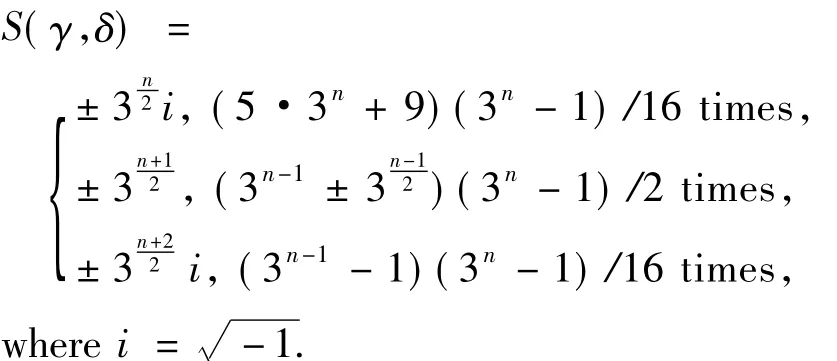
4 An application of the linear code C

Along the research line presented in Ref［4］，［5］，the linear codeCin definition 1 obtained in this paper is very suitable for constructing secret sharing schemeswith interesting access structure.

Definition 2The support of a vectoris defined to be

A codewordc2covers a codewordc1if the support ofc2contains that ofc1.

If a nonzero codewordccovers only itsmultiples，but no other nonzero codeword，then it is called amin-imal codeword.

LetCbe an ［n，k;p］code.If each nonzero codeword ofCisminimal，then such a linear codewill give a secret sharing scheme with interesting access structure described as in Theorem 17 of Ref［4］and Proposition 2 of Ref［5］.

The following Ashikhmin-Barg lemma is useful in determining the minimal codewords for special linear codes.

Lemma 4［4-6］In an［n，k;p］codeC，letwminandwmaxbe the minimum and maximum nonzero weights，respectively.If

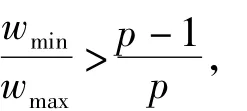
then each nonzero codeword ofCisminimal.

Applying Lemma 4 and Theorem 1，by a direct verification，we have the following proposition.

Proposition 2Ifn≥5，then every nonzero codeword ofCisminimal.

By Lemma 2 and Proposition 2，according to the Theorem 17 in Ref［4］，the secret sharing scheme based onC┴has interesting access structure.

［1］Lidl R，Niederreiter H.Finite fields［M］.MA:Addison-Wesley，1983.

［2］MacWilliams F J，Sloane N J.The theory of error-correcting codes［M］.Amsterdam:North-Holland，1977.

［3］Ness G J，Helleseth T，Kholosha A.On the correlation distribution of the Coulter-Matthews decimation［J］.IEEE Trans Inform Theory，2006，52(5):2241-2247.

［4］Carlet C，Ding C，Yuan J.Linear codes from perfect nonlinearmappings and their secretsharing schemes［J］.IEEE Trans Inform Theory，2005，51(6):2089-2102.

［5］Yuan J，Ding C.Secret sharing schemes from three classes of linear codes［J］.IEEE Trans Inform Theory，2006，52(1):206-212.

［6］Ashikhmin A，Barg A.Minimal vectors in linear codes［J］.IEEE Trans Inform Theory，1998，44(5):2010-2017.