高层建筑考虑脉动风荷载作用下的有限元分析

武黎明

(重庆工商职业学院，重庆400007)

风荷载是高层建筑中水平作用的主要效应之一。在实际工程的正常设计计算时，作用在建筑物上的风荷载沿高度按静力荷载梯形分布或通常按基底弯矩相等的原则［1］，把阶梯形分布荷载转换成等效均布荷载、三角形分布(图1)。根据风荷载的特点，实际工程中的正常设计计算必然与实际存在着差异。基于此，笔者采用有限元软件ANSYS建立10层框架剪力墙简化模型，将其在“考虑脉动风荷载作用”与“正常设计条件”两种情况下的计算结果进行比较分析。

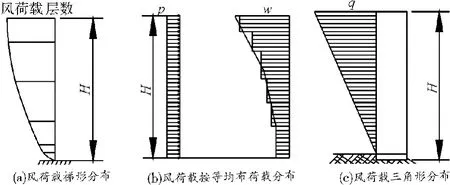
图1 实际工程设计计算的风荷载模型

1 结构概况［1］

某10层钢筋混凝土框架—剪力墙结构办公楼，建筑高度为39.3 m，平面及剖面如图2所示。当地基本风压为0.7 kN/m2，地面粗糙度为A类。结构主要承重构件的截面尺寸及混凝土强度等级如表1。

2 高层建筑有限元模型建立

2.1 材料性质

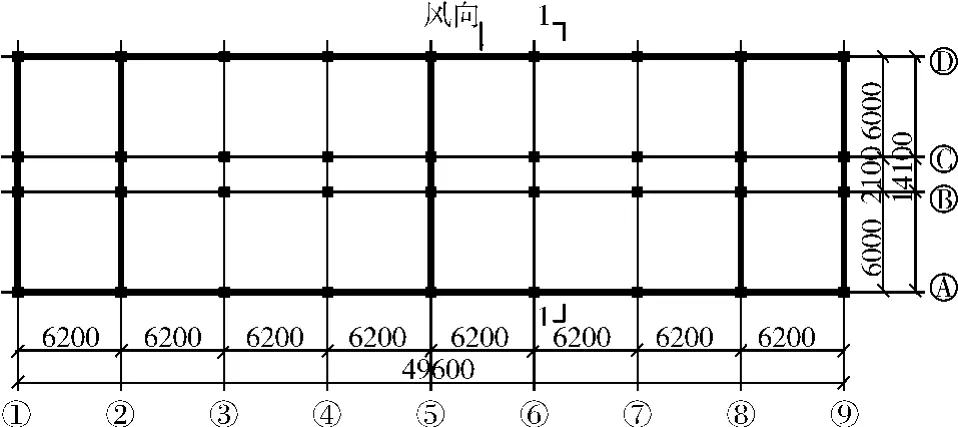
图2 结构平面(mm)

图3 结构立面(m)

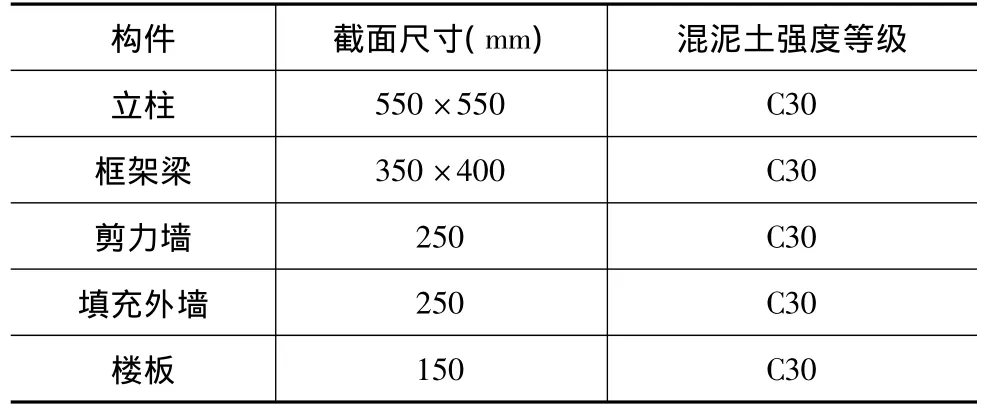
表1 结构参数

在本模型中，为了便于计算，上部结构钢筋混凝土的容重统一采用25 kN/m3，弹性模量为 3.0×1010Pa，泊松比为0.25。填充墙为普通烧结砖，其容重为19 kN/m3，弹性模量根据《砌体结构设计规范》取2.4×109Pa，泊松比为0.2。

2.2 单元类型

在模型中，框架中的梁和立柱均采用BEAM4单元模拟，剪力墙、楼板及外填充墙采用SHELL63模拟。结构有限元模型如图4、图5所示。

图4 框架剪力墙整体模型

图5 框架部分模型

3 风荷载模型的建立

3.1 静风荷载模型

本文的静荷载模型按《建筑结构荷载规范》［4］中常用的阶梯形分布的风荷载换算成等效均布荷载的方法进行计算。得到如图3所示的各层风荷载大小为表2。

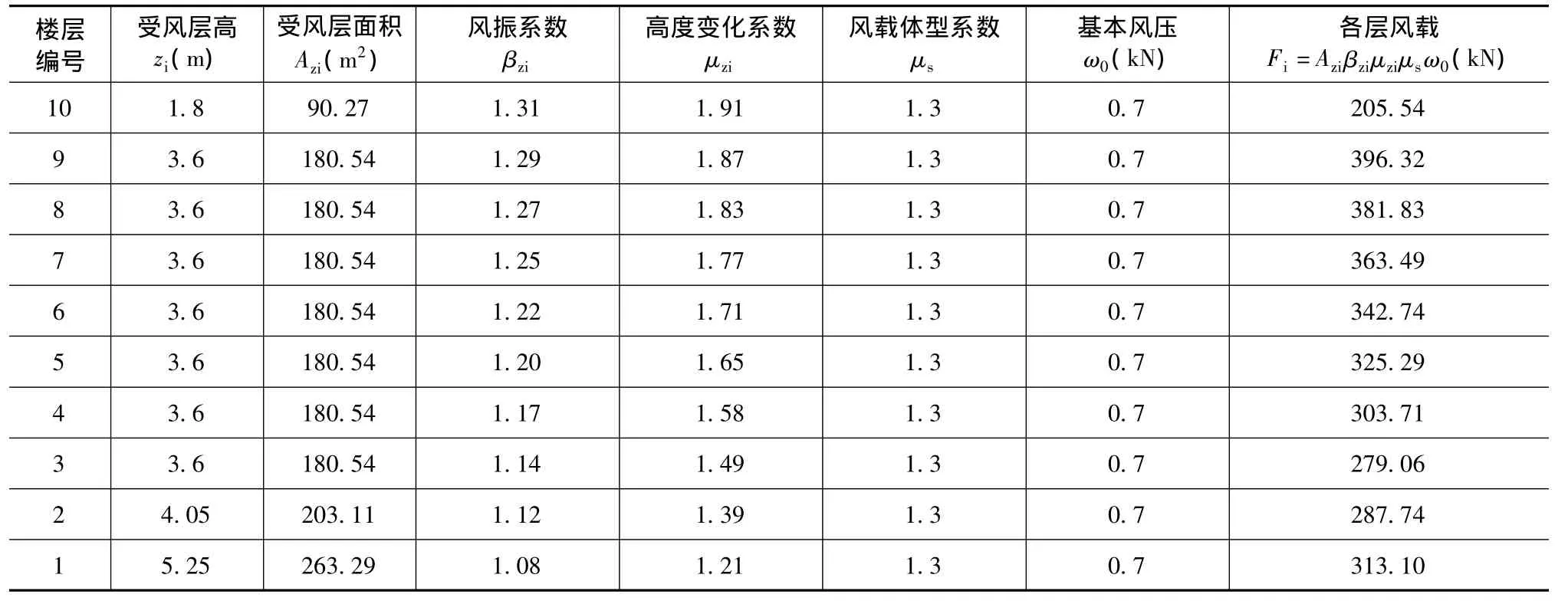
表2 各层风载标准值计算表

根据表3中的Fi/Azi转化面荷载，并加到模型对应高度位置处的迎风面(图8)。

3.2 脉动风荷载模型【5】

为了便于结构设计计算，常常将风速转换为风压来表明风力的大小。低速运动的空气可作为不可压缩的流体看待。对于不可压缩理想流体质点作稳定运动的伯努利方程，当它在同一水平线上运动时的能量表达式为:

式中:WaV为静压能;为动能;C为常数;其中Wa为单位面积上的静压力(kN/m2);V为空气质点的体积(m3);V为风速(m/s);m为运动流体质点的质量(t)。

式(1)两边除以 V，因为 m=ρv，在气压为101.325 kPa、常温15℃和绝对干燥的情形下，γ=0.012018 kN/m3，在纬度450处，海平面上的重力加速度为g=9.8 m/s2，则由自由气流的风速提供的单位面积上的风压为:

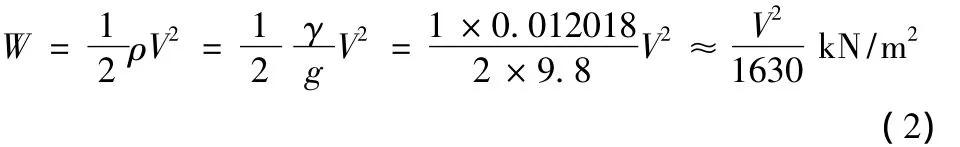
式(2)是在标准大气情况下，满足上述条件后求得的。但由于各地地理位置不同，因而γ和g值也就不同。在自转的地球上，重力加速度g不仅随高度变化，且随纬度的变化而变化。而空气容重γ又是气压、气温和湿度的函数。因此各地的γ/(2g)值均有所不同。上式一般适于内陆海拔高度500 m以下地区，对于内陆高原和高山地区，则随着海拔高度增大而减小。海拔高度到达3 500 m以上地区，γ/(2g)可减至1/2 600;对于东南沿海地区，系数为1/1 750。

根据风速，可以求出风压。但是风速随高度不同而不同，位置愈高，风速愈大，而且周围环境不同，风速亦有不同，因而风速随建筑物所在地区的地质地貌而变化。为了比较不同地区所确定的风速或风压，称为基本风速或基本风压。因为风压对结构受力分析较为直接，所以基本风压在规范中用得比较普遍。

根据上述风载荷模型的假设与简化，本文的风载荷结合当地的水文气象条件采用如下的模型:

该式中k为风荷载模型的修正系数(k的取值根据规范算得的各层风荷载水平力与(3)式括号内所算得的数值，并将此商进行加权平均所得);Y为高度，单位为m;w为激励角速度;q为风压大小，单位为Pa。将所得脉动风荷载函数式(3)通过ANSYS的函数编辑器与函数加载器(图6、图7)把风荷载加到模型的迎风面上。

4 有限元求解结果及分析

图6 函数编辑器

图7 函数加载器

图8 风荷载施加后的模型

?

通过ANSYS软件分析计算得出模型在两种风荷载(模型1为脉动风荷载，模型2为阶梯型风荷载)作用下相同荷载步的整体、楼板、外墙、框架和剪力墙的位移比较，数值比较结果表3所示。由于篇幅，对应的云图不一一列出(图9、图10)。

从上面的比较结果可以看出，在相同的材料、尺寸，不同的风荷载模型作用下，风荷载模型1中的整体、框架、楼板、剪力墙节点的最大位移及结构所受的内力(剪力、轴力、弯矩)总体上均大于模型2。因为脉动风荷载是周期性的动荷载，在水平方向除了按静力荷载作用于结构外还要附加惯性【7】力，所以对结构内力和位移产生影响。

5 结论及建议

通过对高层建筑在“考虑脉动风荷载作用”与“正常设计条件”两种情况下的ANSYS三维仿真分析结果的比较，得出如下结论及建议:

(1)脉动风荷载对高层建筑结构的内力与变形都有不同程度的影响，其对结构的剪力墙部分影响较大。

(2)实例的脉动风荷载与正常设计下的阶梯型静风荷载计算的内力和变形相差不大，在特定的风荷载与建筑高度下设计的结构还是比较符合实际的。但这一现象是否能在多数高层框架剪力墙结构中普遍存在，还有待在更广泛的范围内对更多具体结构进行进一步的分析研究。

(3)建议在结构抗风设计中，尤其是需要考虑脉动风效应时，不能完全把风荷载等效成静风荷载来考虑，要结合当地的水文气象及建筑物的高度等综合考虑，以使设计更加合理。

图9 两种模型延风向的位移对照云图

图10 两种模型外墙位移对照云图

(4)本文仅从周期性的脉动风荷载与静风荷载比较来说明“正常设计条件”时与实际存在的差异，并没有考虑到建筑物的高度、结构自身的频率及“桩－土－上部结构”共同作用等因素的影响。所以想要更加清楚的认识实际风荷载对高层建筑结构的影响，还需进一步改进模型，提高其真实性。

［1］施岚青.一、二级注册结构工程师专业考试应试指南［M］.北京:中国建筑工业出版社，2009

［2］李围.ANSYS土木工程应用实例［M］.北京:中国水利水电出版社，2007

［3］JGJ 3－2002.J 186－2002高层建筑混凝土结构技术规程［S］

［4］程文滚.混凝土结构［M］.北京:中国建筑工业出版社，2002

［5］龙驭球，包世华.结构力学教程［M］.北京教育出版社，2006

［6］刘晶波，杜修力.结构动力学［M］.机械工业出版社，2005

［7］郝文化.ANSYS土木工程应用实例［M］.北京:中国水利水电出版社，2005

［8］JGJ 3－2002高层建筑混凝土结构技术规范［S］

［9］GB 50009－2002建筑结构荷载规范［S］