考虑道路景观效应的改进广义用户平衡和广义系统最优配流模型

金龙祥，左仁广

(1.云南省泸西县交通局，云南泸西652400;2.中铁二院工程集团有限责任公司，四川成都610031)

随着现代化社会的发展，城市中的交通问题不容忽视，各大城市的交通拥堵问题的解决刻不容缓。持续性的交通拥堵及其带来环境污染等一系列社会问题，严重阻碍了城市经济的持续健康发展。通过扩建路网，加宽道路，限制出行等方式并不能从根本上有效解决交通拥堵问题。为了增加现有道路的使用效率，合理分配交通流，笔者对交通网络进行分析。从考虑环境因素的广义用户平衡和广义系统最优配流模型方面来进行交通网络分析具有很大的理论意义和现实意义。其模型的建立反映了随着交通事业发展，环境污染严重的现实问题。

针对城市道路所附带产生的严重的环境污染问题，景观道路被相应地提出。景观道路在注重绿化环境的同时，还提高了城市的文化层次，使得人们的出行不仅成为生存需要而且能够有美的享受。客观地量化评价景观道路给人带来的舒适感、美感，以及其对人们出行方式的影响和对路网交通流分配的影响，对整个城市绿化和文化环境的提升以及路网的规划建设，都有重要的意义。本文通过将景观道路的景观效应用广义交通网络分析来阐述其对路网配流的影响。

1 改进模型建立［2］

网络包含两个基元，即节点集合和连接节点的弧的集合。在交通网络中，交叉口或行驶终端即为节点，连接节点的路段即为弧。弧上的阻抗或者服务质量包含多项内容:行驶时间、安全、成本和舒适度等。在以往的交通网络分析中，一般将时间作为唯一的计量标准。因为在过去出行通常作为生存需要的时候，时间是影响人们出行选择的最主要因素。人们的出行时间影响生存需要(如上班)。但是现在人们的出行目的有所不同，尤其是目前私家车日益普遍的情况下，有相当部分的车辆出行不是出于生存需要，而是出于生活需要(如旅游)。此时影响其出行路线选择的将不再是单纯的时间长短。污染严重与否，沿线风光如何，行驶的舒适性、安全性，线型是否流畅，信号控制的多少等等都成为影响车辆出行选择的重要因素。

考虑到上述内容，笔者以出行费用作为目标函数。假定传统的配流技术能适用于考虑和公平目标的路径选择分析，实现上述配流问题所需的唯一变化就是要寻找合适的广义费用函数。在广义费用函数中，不仅包括出行时间、安全性、舒适性等因素，还应考虑环境因素和文化景观效应的影响。

一般广义费用方程为:

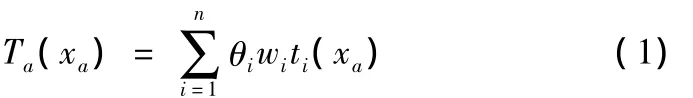
式中:n为广义费用函数中所考虑影响因素的个数;ti(xa)为路段a上一辆车产生的第i种费用的量，其值可以根据不同地区的实际情况用统计的方法得到;θi为权重系数，且为模型参数，起转化量纲的作用。

这里对一般广义费用方程进行改动。

方程原型仍为

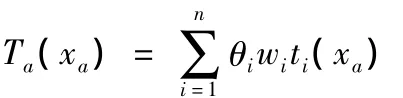
式中:θi为权重系数，且，其中θi不需要大于等于0。其他各项如上。

在实际分析中，具体用t1(xa)表示一辆车在路段a上的行驶时间，它是传统配流方法的主要依据，实际中最简单也最常用的计算公式是由美国公路局(U.S.BureauofPublicRoads)提供的，即

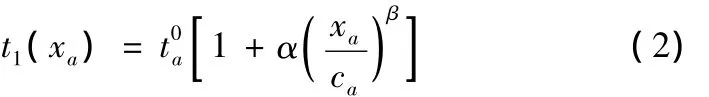
式中:xa为路段a上的交通流量;t0为零流阻抗，亦即路段上流量为零时一辆车自由行驶所需的时间;ca为路段a上的实际容限，即实际通过能力，通常称xa/ca为拥挤系数。α、β为模型参数，一般取α=0.15，β=0.14，α、β值根据实际情况(如路段的长度、宽度)可以作相应调整。

t2(xa)表示路段上汽车产生的尾气以及噪音等污染。汽车尾气的有害成分较多经常采用TRANSYT72F模型给出的关系进行分析，该模型的一般函数关系是

式中:Ra为路段a上交通污染物排出率［g/(veh·m)］;va为路段a上的平均速度(m/s);B、C、D为常数。

假设每条路段上车辆的速度是不变的，并且所有路段的坡度为零，车辆在每条路段上的行驶速度va是由路段长度la除以车辆行驶时间t1(xa)得到的。在给定路段a上一辆车产生的污染物的总量t2(xa)可由污染物排放率乘以路段Ra距离la得到;进一步可得到路段a上车辆尾气的总量xat2(xa)，即

式(4)适用于计算燃料消耗，CO、NO、烃类物质及硫的化合物等的排放量。交通配流中通常根据CO的排放率进行，这是因为:①污染物的排放率在形式上是类似的，从而基于不同污染物排放率得到的配流结果应该相同;②通常认为CO是一种危害性最强的污染物，其排放水平需要降低。下式给出了在分析中用到的CO排放率的函数形式

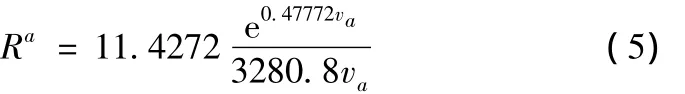
式中:Ra为路段a上的CO排出率［g/(veh·m)］;va为路段a上的平均速度(m/s)。

可类似地考虑噪声影响因素的大小。

这里引进文化、景观效应的量化指标t3(xa)，其意义为在一定等级的景观效果道路上行驶给人带来的舒适感量化指标。即使需要花更长的时间到达目的地，但是因为相应的景观效应使得驾驶人的心情愉悦，而使得心理驾驶时间缩短。变相的使得此路段的最小行驶阻抗降低。在费用模型中，θ3≤0，意为景观效应给驾驶人带来的舒适感和美感，以货币形式量化，作为道路返还给使用者的货币，相当于商场里给顾客的购物优惠券。这样就变相减少用户总体费用。

因目前景观道路的等级划分及其具体的景观效应量化水平的确立尚无成熟理论，此处则尝试对其等景观水平划分和景观效应量化进行数学规划。此数学规划要基于现场的测试数据。

式中:K由现场实测污染状况和道路景观等级l(l按道路绿化面积与道路占地面积比例以及文化景观水平按比例权重)确定;c为道路上的交通流量，0≤c≤c0:(从社会总体收益最大化来看，路网容量存在一个最优使用量c0，当c＜c0时，e(c)＞0;每辆车使用单位路网容量所获得的收益为e(C)，当 c＞c0时 e(c)＜0)。［3］u'rs为该道路的最小行驶阻抗，即交通量为0时，行驶该道路所使用的时间。urs为传统的网络平衡分析中的最小的行驶阻抗。

将现场测得数据与相关理论数据结合推导出K的值。这样就建立了景观道路景观效应量化水平数学规划。当然此方程的具体可使用性要在相关数据获得的情况下再进行深入的研究讨论。

2 GUE配流模型和GSO配流模型

有了广义费用模型的改进则相应给出改进GUE配流模型和改进GSO配流模型。

2.1 采用符号

N为网络节点的集合;A为网络路段的集合;R为产生运量的起始节点的集合，R＜N;F为吸收运量的终讫节点的集合，F＜N;r为一个起始节点，r∈R;s为一个终讫节点，s∈F;Krs为连接O－D对r－s的所有路径的集合;qrs为所研究时段内从r到s的交通需求量;xa为路段a上的交通需求量，a∈A;t2(xa)为路段 a上的广义总费用为连接O－D对子r－s之间路径k上的流量为连接O－D对子r－s之间路径k上的广义费用为若路段a在连接O－D对子r－s的路径k上，其值为1。否则为0。

关于路段与路径之间的流量和广义费用，有如下关系(图1)。

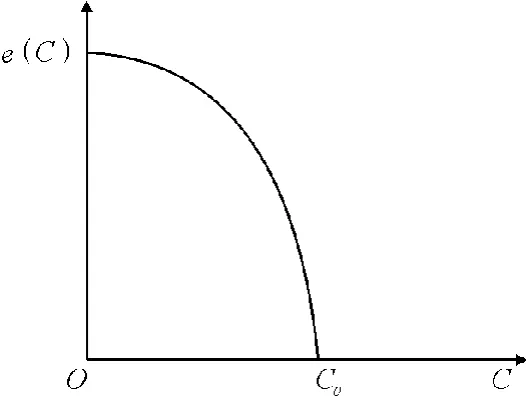
图1 汽车使用者边际收益示意［3］

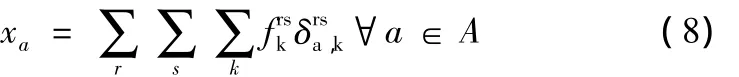
式(7)、式(8)为路段与路径的关联关系。

2.2 GUE配流模型

据以上符号，及以上对于广义费用模型的改进，能够得到:改进GUE配流问题等价于如下的数学规划问题

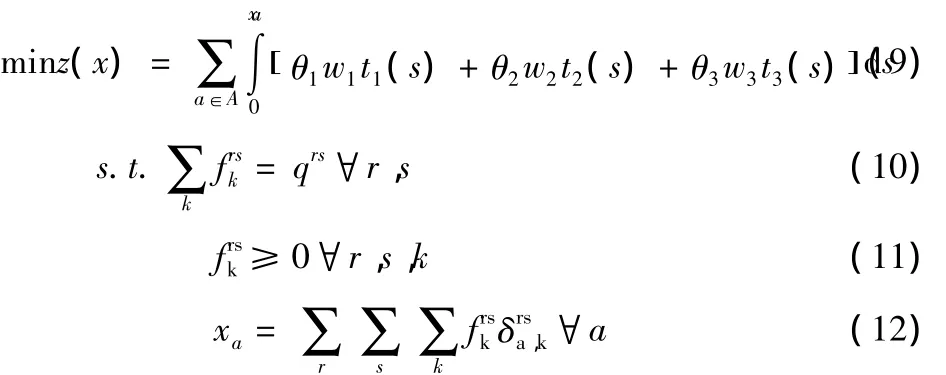
令

则目标函数变为

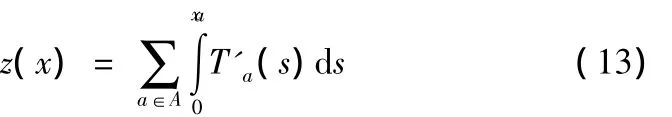
式(10)表示路经流量与O－D需求量之间的守衡关系，式(11)是路径流量的非负约束，而式(12)是路段流量与路径流量的关联关系，有:

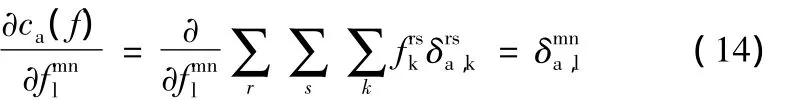
M1是一个带线性等式和非负约束的极小值问题，其LAGRANGE函数为

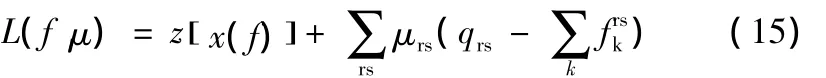
M1的一阶条件等价于 L(f，μ)极小一阶条件，同时式(11)成立。与传统配流模型的等价性证明类似，容易证明M1的解是等价于GUE条件的解。下面讨论唯一性条件，M1的约束集是凸的，若目标函数也是凸的，则M1是一个凸规划问题，从而最优解唯一。但是由于考虑了车辆尾气的影响和噪声水平等其它因素，广义费用函数一般不再是路段流量的增函数，从而z(x)的HESSIAN矩阵▽2z(x)不一定是正定的，路段流量和最优解也不一定唯一。由于实际问题要解决的是考虑环境因素和公平目标配流问题解的存在性和可行性问题，故暂可认为这并不影响本文的讨论。

2.3 GSO配流模型

为了便于比较，下面给出考虑环境因素的GSO配流模型，其等价的数学规划问题是

M2被称为广义系统最优规划公式，系统最优原则假设驾驶员接受统一调度，大家的共同目标是使系统总的广义费用最小，而在GUE规划中，每位驾驶员只从自身利益出发去寻找广义费用最小的路径，因此，通常情况下，GSO的解不是一个GUE的解。

3 算法

从形式上看，M1是一个标准的UE模型，故可以用传统的求解算法求解。下面给出在实际中常用的求解固定需求平衡配流模型的F－W算法:

第4步:寻找迭代步长。求解一维极小值问题

st0≤α≤1假设求得步长为αn

第5步:更新流量。置

第6步:收敛性检查。如果满足收敛性准则，若

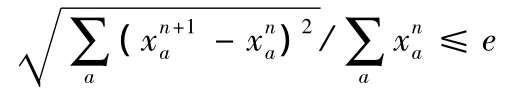
则算法终止，否则令n=n+1，转第2步，其中e是与现给定的迭代精度。

4 结束语

当代交通需求不断增长，道路通行能力不得不进行相应的提高。对现有的路网进行优化改造。建立合理的广义费用函数，可以用传统的配流方法求解考虑环境因素和景观效应以及公平目标的GUE模型和GSO模型，规划人员或者可以根据实际情况调节权重值，在广义费用函数中的不同影响因素之间取得均衡。道路使用者对行驶路径的选择做出更加有利于整个路网有效使用。从研究中可以看出，景观道路对于路网规划，以及网络平衡配流的实际意义。因此对于道路景观建设可以从网络平衡分析层面上进行更深入的讨论研究，进一步扩展景观道路的经济意义和社会价值。本文主要得到的成果有:

(1)介绍改进广义用户平衡和广义系统最优配流模型的理论背景及其理论框架。

(2)引进文化、景观效应的量化指标t3(xa)，其意义为在一定等级的景观效果道路上行驶给人带来的舒适感量化指标。

(4)目前景观道路的等级划分和其具体的景观效应量化水平的确立尚无成熟理论。需要进一步进行研究，来完善考虑道路景观效应的改进广义用户平衡和广义系统最优配流模型。

［1］黄海军.城市交通网络平衡与分析［M］.人民交通出版社，1993

［2］杨文国，高自友.考虑环境因素的广义用户平衡和广义系统最优配流模型［J］.中国公路学报，2003，16(4)

［3］许薇，贾元华.城市道路交通拥堵问题的博弈分析［J］.交通科技，2006(2)