激励参数对2K－H行星轮系动态响应的影响

孙首群 赵玉香 徐 伟 杨 凡 杨 炎

上海理工大学，上海，200093

激励参数对2K－H行星轮系动态响应的影响

孙首群 赵玉香 徐 伟 杨 凡 杨 炎

上海理工大学，上海，200093

采用集中质量法构建了混合动力汽车行星齿轮减速机构多自由度弹性动力学模型。在综合考虑时变啮合刚度、综合齿频误差以及齿侧间隙激励条件下，借助自适应变步长五阶Runge－Kutta法求解该多自由度振动系统的非线性动力学方程。通过位移和动载荷的时间历程、相图、FFT、Poincaré映射等途径，获得了系统的动态响应和齿间动载特性，并分析了系统各激励参数对动态响应的影响。结果表明，激励频率、齿侧间隙、外载荷等激励参数对系统动态响应影响巨大。

2K－H行星齿轮；参数激励；非线性动力学；动态响应

0 引言

近20年来，国内外研究者在齿轮上尤其是在行星轮系非线性动力学的研究上已经取得了很多成果［1－7］。由于行星齿轮机构同时有多对齿轮副外啮合和（或）内啮合，因而这实际是一个串并联多自由度动力系统，其非线性响应非常复杂。Parker等［8］用有限元法研究了行星齿轮系统非线性动态响应，Sun等［9］用谐波平衡法研究了行星轮系的幅频特性，孙智民等［10－11］用数值方法研究了星型轮系纯扭转模型的非线性动力学特性。但是，上述研究成果中有的建模过程简化较多，有的对多种外载因素变化的综合影响考虑不够全面，有的对系统的非线性响应特性的分析不够深入、细致。鉴于以上情况，本文同时考虑齿侧间隙、综合误差、时变刚度等因素的综合影响，对2K－H行星轮系多自由度复杂动力学系统强非线性动力学行为进行深入细致地分析和研究。

2K－H行星轮系作为一个参数激励系统，各激励参数怎样影响动态响应，不同激励参数下系统啮合状态会发生怎样变化，都有待深入研究。了解参数在系统的整个动力学行为中所起的作用，有助于更加深入地了解系统的振动机理，掌握系统的动力学特性，寻求降低齿轮振动的措施，从而提高齿轮传动的动态性能。

本文以混合动力汽车双电机驱动系统的主减速器为研究对象，运用集中质量法构建了混合动力汽车行星齿轮减速机构多自由度弹性动力学模型，借助变步长自适应Runge－Kutta法进行求解。在不同参数激励变化下对系统动态响应进行详细而深入的分析和研究，并进一步研究其动态特性及啮合振动产生的动载荷，对减小振动与冲击、降低噪声、延长工作寿命、保证工作可靠性等方面有重要意义。

1 行星齿轮减速器物理模型

图1是混合动力汽车双电机驱动系统示意图。其工作原理是：汽车正常行驶时，主电机5高速运转，单向离合器4分离，系统动力全部由主电机5通过主减速器6提供，辅助电机7的一端带动辅助减速器3空转，另一端通过皮带轮1带动空调2运转；当汽车爬坡等动力不足时，主电机5转速降低，单向离合器4在主电机5转速降低到预设值时接合，辅助电机7与主电机5共同向汽车提供动力，从而有效改善了汽车爬坡时的动力性能。

图1 双电机驱动系统示意图

本文研究对象为主减速器6，其机构简图见图2。该机构中，太阳轮s与行星轮p为外啮合，行星轮p与内齿圈r为内啮合，内齿圈r固定在机架上。动力从输入轴h输入，通过行星架c传递到输出轴l。图3为该机构的弹性力学模型图。

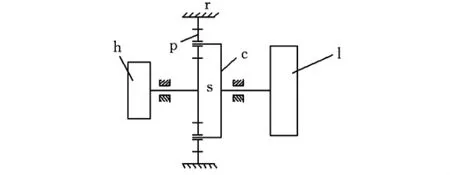
图2 2K－H行星轮系传动机构简图

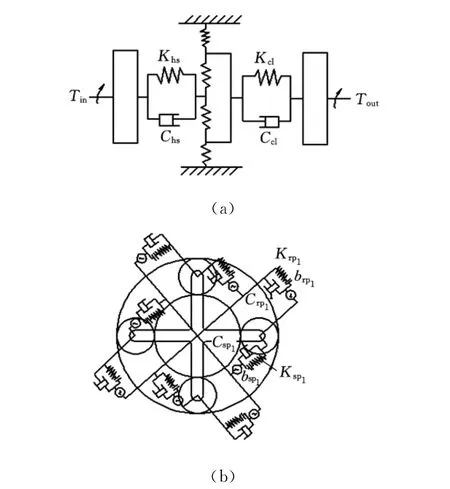
图3 行星轮系力学模型图

2 行星轮系非线性动力学模型

2.1 动力学方程

以输入转矩作用下各个构件产生的运动方向为各自角位移相应的正方向，定义啮合线上的等价线位移时也以输入转矩作用下的运动方向为正方向，而对于各个啮合作用线上的相对位移x，则规定齿面受压时其为正方向。

下面针对图2和图3所示的行星齿轮减速器进行受力分析，建立弹性动力学方程。

设φn为回转角，Rbn为基圆半径，Jn为转动惯量，其中下标n表示各元件的代号。

根据啮合关系知，太阳轮s与行星轮p的相对位移ΔSsp和行星轮p与内齿圈r的相对位移ΔSrp分别为

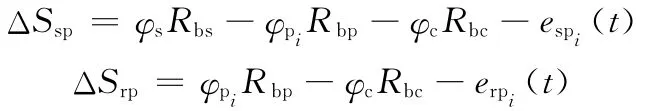
式中，下标pi表示第i个行星轮。

设P、D分别为齿轮副的弹性啮合力和黏性啮合阻尼力，则有

应用拉格朗日方程，建立八自由度的扭转振动模型，其中扭转自由度分别为φh、φs、φpi、φc、φl。图3所示系统的动力学微分方程如下：

式中，Jceq为行星架等效转动惯量；mp为行星轮的等效质量；α为压力角；mh、ms、mpi及ml分别为主轴（齿轮轴）、太阳轮、第i个行星轮及行星架的当量质量；Rbc为行星架当量半径。

角位移与啮合线上的线位移转换式如下：

则可将上述方程组转换为关于以上10个坐标的方程，写成状态方程为

式中，X（t）为系统位移列矩阵（10×1）；M 为系统的质量矩阵（10×10）；C为系统的阻尼矩阵（10×10）；K为系统的刚度矩阵（10×10）；f为系统间隙非线性函数列矩阵（10×1）；F（t）为系统载荷列矩阵（10×1）。

2.2 系统量纲一处理

定义量纲一时间自变量τ＝ωnt，同时引进位移标称尺度bc＝1μm，通过量纲计算可得出其他量纲一表达式：

为叙述方便，以下各量纲一符号不再加上划线，未特别说明的各物理量，均为量纲一量。

3 求解与分析

3.1 方程求解

对间隙型非线性微分方程（式（9）），采用变步长五阶Runge－Kutta法求其数值解，并针对混合动力汽车双电机驱动系统的主行星减速器（内含4个行星轮）进行计算。该2K－H行星齿轮传动系统的部分原始参数见表1。

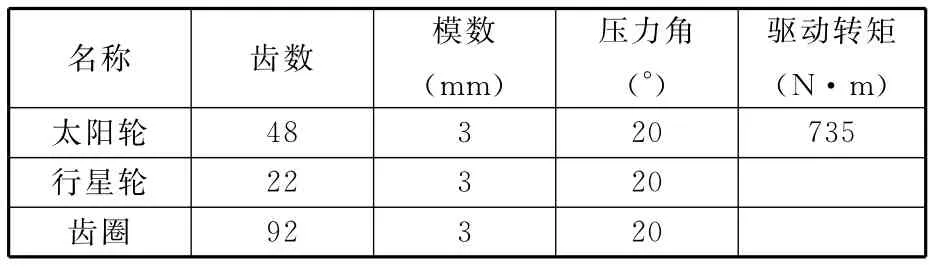
表1 2K－H行星齿轮减速器原始参数

考虑初始值的影响，为消除系统的瞬态响应，需要将开始的数百个周期略去，这样才能得到效果理想的相图、Poincaré映射图等。求解时，每个啮合周期划分为200个等分，相对误差控制为10－6，绝对误差控制为10－8。以稳态响应的时间序列为基础，获得了该动力系统的位移时间里程图、相图、Poincaré映射图、FFT谱图等。以下结果均为太阳轮与行星轮的啮合时的结果，行星轮与内齿圈的啮合类似，限于篇幅本文不再赘述。

3.2 激励频率对动态响应的影响分析

取啮合阻尼比ζ＝0.02，改变激振频率Ω，分别得到系统的稳态响应如图4～图8所示，其中，f为行星轮系统的横向振动频率。

由图4可知，在Ω＝0.3时，系统为简谐响应，位移时间历程为标准正弦波，相图为标准椭圆，Poincaré映射为单个离散点，FFT频谱只出现在激励频率Ω上，这和线性系统得到的结果相同，即单频激励单频响应。

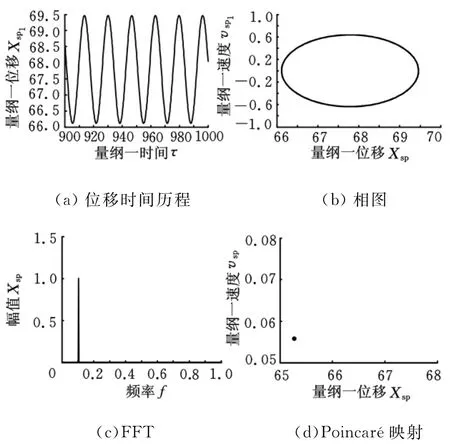
图4 简谐响应（Ω＝0.3）

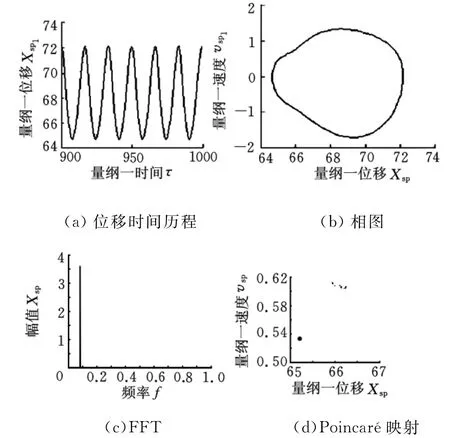
图5 单周期非简谐响应（Ω＝0.38）

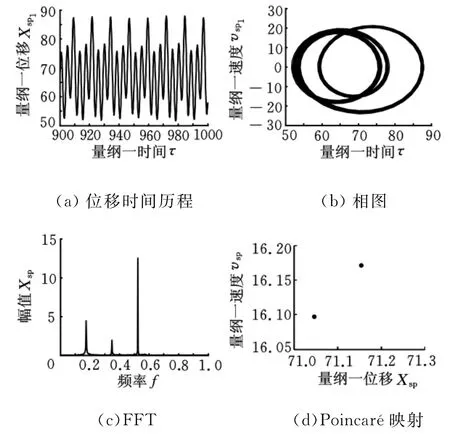
图6 周期二次谐波响应（Ω＝0.5）

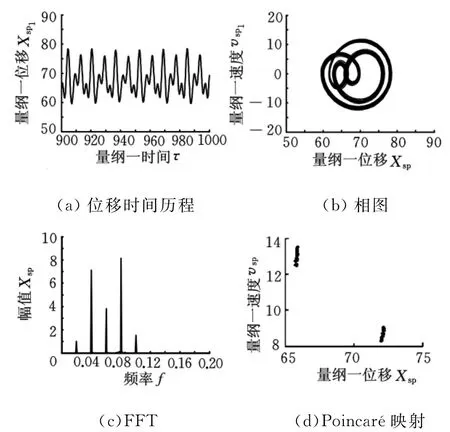
图7 拟周期响应（Ω＝0.78）

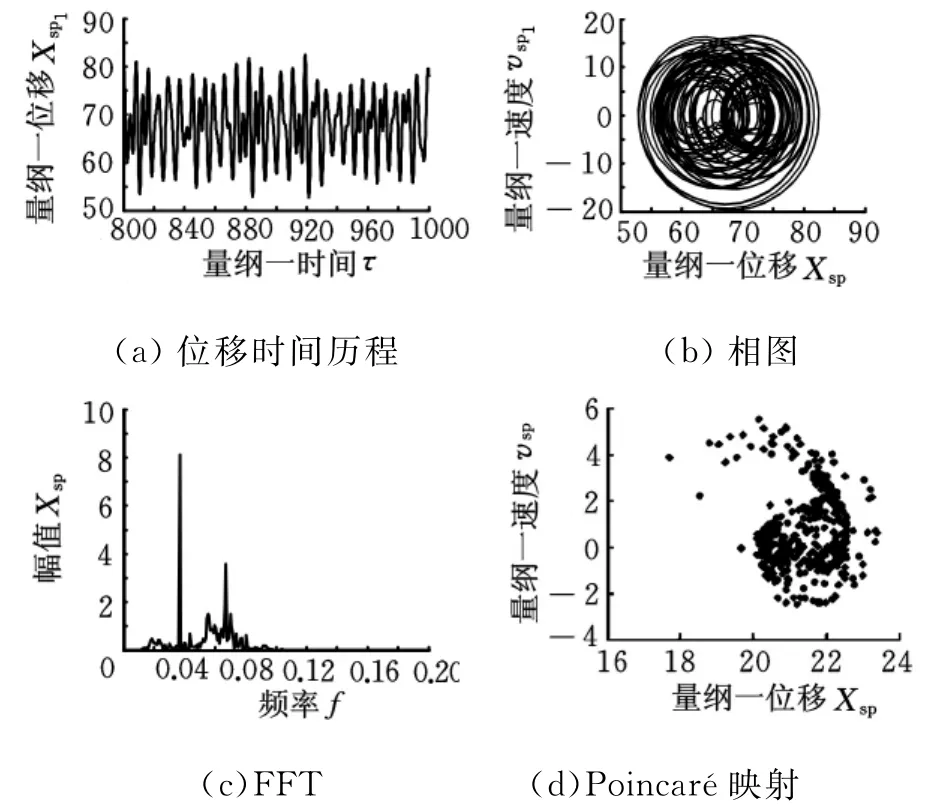
图8 混沌响应（Ω＝0.85）

如图5所示，系统响应为非简谐单周期响应，此时的位移时间历程仍为单周期运动，但相图为非椭圆单环闭合曲线，Poincaré映射依然为单个离散点。在Ω＝0.5时，系统为周期二次谐波响应（图6），此时响应的时间历程为频率为Ω／2的周期运动，Poincaré映射包含2个离散点，而FFT频谱分布在多个离散点上。在Ω＝0.85时，系统出现了混沌响应（图8），此时的位移时间历程为非周期的，Poincaré映射为无穷多个片状的密集点，而其FFT频谱是具有一定宽度的连续谱。

以上在不同激励频率条件下得到了系统5类稳态响应，即简谐响应、单周期非简谐响应、周期二次响应、拟周期响应以及混沌响应，各种稳态响应分别具有不同的特征。具有超谐或次谐成分的周期响应、拟周期响应和混沌响应是无法用线性系统理论得到的。由此可见，将非线性振动理论用于行星传动系统的动态特性分析与研究中，可得到更为细致和深入的结果。

3.3 齿侧间隙对动态响应的影响

参数取Ω＝0.8，量纲一内啮合力矩Tin＝1130，啮合阻尼比ζ＝0.02，改变齿侧间隙b，分别得到系统的动载荷和相轨迹如图9～图14所示。

图9 b＝0的动态响应

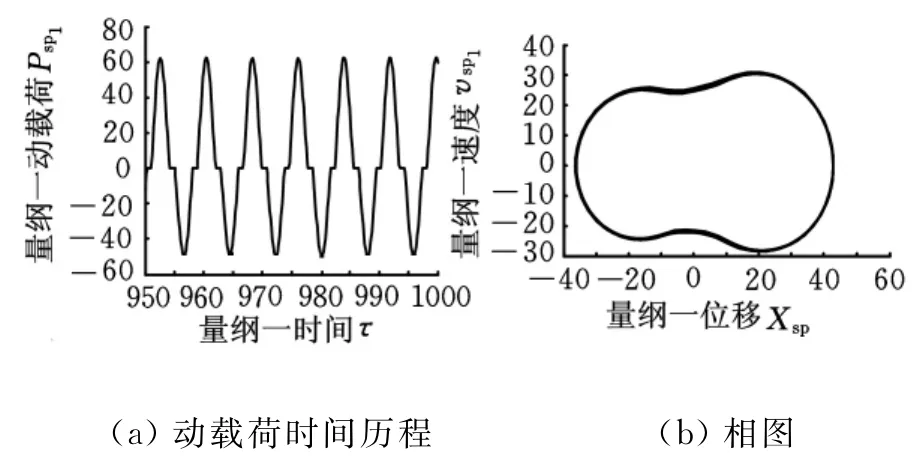
图10 b＝10的动态响应

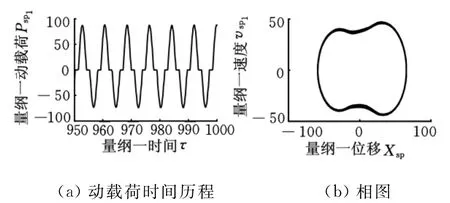
图11 b＝20的动态响应

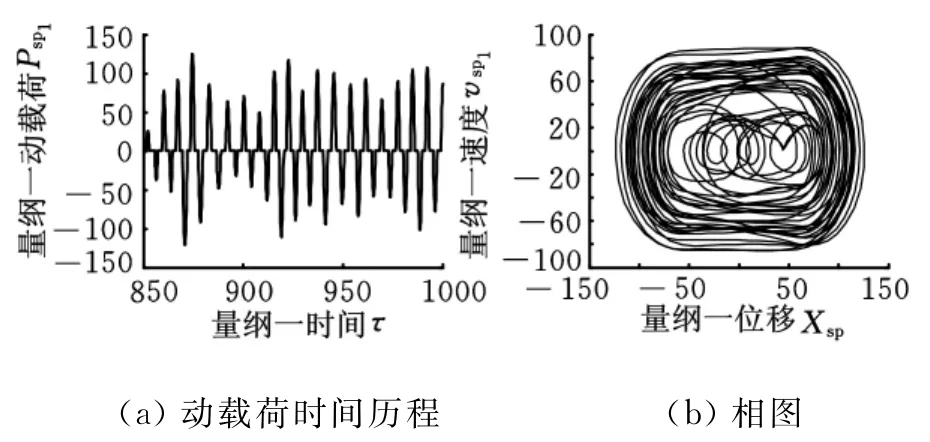
图12 b＝60的动态响应

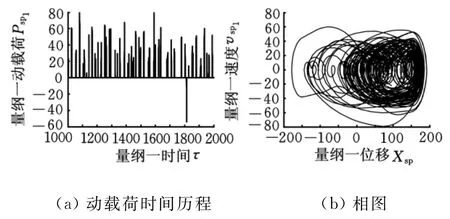
图13 b＝150的动态响应

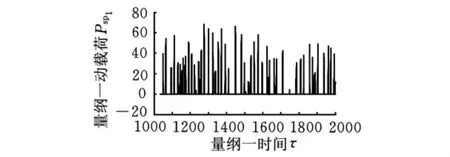
图14 b＝200的动态响应

分析图9可知，无间隙时系统为线性系统，其稳态响应为简谐响应，动载荷为正弦波，相图为标准椭圆，说明系统处于无冲击状态。分析图9～图11可知，量纲一齿侧间隙小于40.5时相图均为非椭圆封闭单环曲线，说明系统的稳态响应为单周期非简谐响应，太阳轮与行星轮的啮合处于双边冲击状态，且随着齿侧间隙的增大，动载荷的最大值也随之增加，振动加剧。当齿侧间隙为60时系统响应变为拟周期响应，啮合处于双边冲击状态（图12）。齿侧间隙大于150时系统响应为混沌响应，系统仍处于双边冲击状态但有向单边冲击过渡趋势，齿背冲击出现的频率和延续的时间越来越少，各齿轮副之间的啮合状态分别由双边冲击状态逐渐向单边冲击状态转化（图13）。系统在量纲一齿侧间隙为200时各齿轮副处于单边冲击状态，此后再增大齿侧间隙，各齿轮副啮合状态不再变化，而且其动载荷系数仅有微小变化。

由以上分析可见，当齿侧间隙变化引起行星齿轮传动的齿轮副啮合状态在无冲击、单边冲击、双边冲击之间转化时，系统响应就会发生突变或分岔甚至混沌。在一定的齿侧间隙范围内，间隙的改变对系统的动态特性只有一些量上的改变，没有质的影响，齿轮副之间的啮合将保持在特定的啮合状态。但在一些临界点处，响应是非常敏感的。总体上讲，假如在齿侧间隙较小时齿轮副的啮合状态出现齿背冲击，那么随着间隙的不断增大，会趋向仅发生脱齿的单边冲击状态。当间隙达到某一上限值时，齿轮副的啮合状态将保持单边冲击状态，并且系统的响应也不再发生大的变化。

3.4 外啮合扭矩对动态响应的影响分析

参数取Ω＝0.8，啮合阻尼比ζ＝0.02，齿侧间隙b＝100，改变量纲一外啮合扭矩Tout，分别得到系统的动载荷和相轨迹如图15～图16所示。

由图15和图16可知，在扭矩较小时，系统响应为混沌响应。当弹性啮合力保持大于0时，齿轮副的啮合为正常啮合，无冲击发生；当弹性啮合力出现0值而无负值时，说明轮齿之间无弹性啮合力，齿轮副接触处于脱齿状态；而弹性啮合力出现负值时，表明齿轮副以齿背进行接触，相应的齿轮副有齿背冲击现象发生。在图15中齿轮副的最大动载荷很大，各齿轮副均处于双边冲击状态。当扭矩为950时系统仍为混沌响应，但齿轮副之间的啮合状态有所变化，太阳轮与行星轮变为正常齿面啮合，不存在齿背啮合，处于无冲击状态。

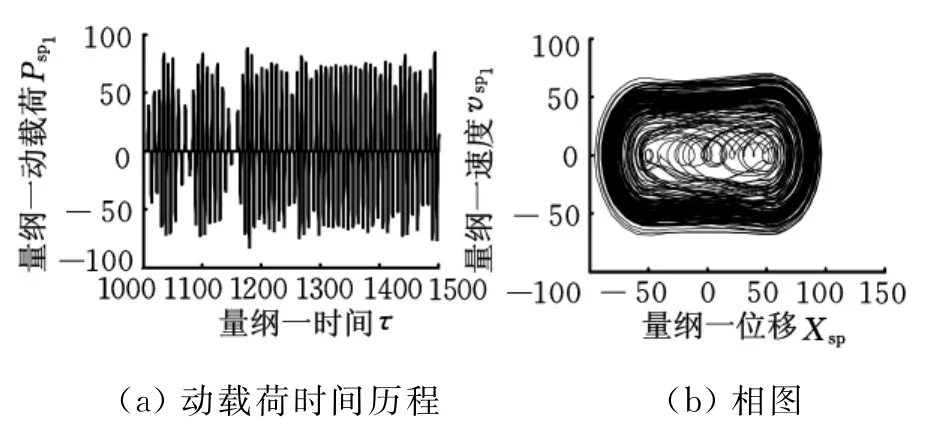
图15 Tout＝50的动态响应

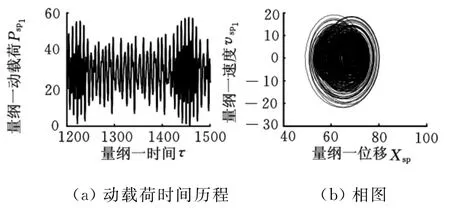
图16 Tout＝950的动态响应

进一步计算分析表明，继续增大负载，齿轮副的啮合状态不变，动载荷略有增加，系统响应出现跳跃，逐渐由混沌响应转化为非简谐两周期运动。进一步增大负载，系统响应有转变为标准简谐响应的趋势。

此结果与文献［10－11］等在相近条件下的实验与理论分析的结果基本一致［12］，从而说明本文研究方法是有效和可靠的。

4 结论

（1）不同激励频率使得系统经历了5类稳态响应，即简谐响应、非简谐单周期响应、周期二次响应、拟周期响应以及混沌响应，各种稳态响应分别具有不同的特征。

（2）增大齿侧间隙行星轮系的齿轮副啮合状态逐渐由无冲击经历单边冲击向双边冲击转化，在此过程中系统响应会产生突变或分岔以至混沌。在一定的齿侧间隙范围内，间隙的改变对系统动力学行为只有一些量上的改变，没有质的影响，齿轮副之间的啮合状态保持不变。

（3）增加负载使系统中各齿轮副的啮合状态逐渐经历双边冲击、单边冲击到无冲击状态的过渡。每发生一次啮合状态的变化，系统响应必然出现质的飞跃。

［1］ 李润方，王建军.齿轮系统动力学－振动、冲击、噪声［M］.北京：科学出版社，1997.

［2］ 刘梦军，沈允文，董海军.单级齿轮非线性系统吸引子的数值特性研究［J］.机械工程学报，2003，42（4）：402－407.

［3］ 卢剑伟，刘梦军，陈磊，等.随即参数下齿轮非线性动力学行为［J］.中国机械工程，2009，20（3）：330－333.

［4］ 王晓笋，巫世晶，周旭辉，等.含侧隙非线性齿轮传动系统的分岔与混沌分析［J］.振动与冲击，2008，27（1）：53－56.

［5］ 庞茂，周晓军，杨辰龙.汽车主减速器非线性振动特性仿真［J］.浙江大学学报（工学版），2009，43（3）：559－564.

［6］ Al－shyyab A，Kahraman A.Non－linear Dynamic Analysis of a Multi－mesh Gear Train Using Multi－term Harmonic Balance Method：Period－one Motions［J］.Journal of Sound and Vibration，2005，284：151－172.

［7］ 唐进元，陈思雨.阻尼和刚度项含时变参数的强非线性振动系统周期解研究［J］.振动与冲击，2007，26（10）：96－100.

［8］ Parker R G，Agashe V，Vijayakar S M.Dynamic Response of a Planetary Gear System Using a Finite Element／Contact Mechanics Model［J］.Transactions of the ASME，Journal of Mechanical Design，2000，122（3）：305－311.

［9］ Sun Tao，Hu Haiyan.Nonlinear Dynamics of a Planetary Gear System with Multiple Clearances［J］.Journal of Mechanism and Machine Theory，2003，38：1371－1390.

［10］ 孙智民，沈允文，王三民，等.星型齿轮传动系统的非线性动力学分析［J］.西北工业大学学报，2002，20（2）：222－226.

［11］ 孙智民，季林红，沈允文.2K－H行星齿轮传动非线性动力学［J］.清华大学学报（自然科学版），2003，43（5）：636－639.

［12］ 赵玉香.行星齿轮减速器非线性动力学研究［D］.上海：上海理工大学，2009.

Impacts of Exciting Parameters on 2K－H Planetary System Dynamic Response

Sun Shouqun Zhao Yuxiang Xu Wei Yang Fan Yang Yan
University of Shanghai for Science ＆ Technology，Shanghai，200093

Elastodynamics model of multi－DOF system for planetary mechanism in the hybrid electric vehicle was founded by the method of lumped mass.The nonlinear dynamics equations of vibration system with the excitation of time－varying mesh stiffness，gear composite errors and clearances were solved by the method of the 5－steps self－adaptive Runge－Kutta.As a result，the dynamic response and behaviors of dynamic load between teeth of the system were acquired by combining with displacement or dynamic load，phase plane，FFT，Poincarémapping.Then，impacts of exciting parameters on system dynamic responses were analyzed.The numerical results indicate that frequency，backlash or external load has huge influence on system dynamic response.

2K－H planetary；parameter excitation；nonlinear dynamics；dynamic response

TH132.4

1004—132X（2011）01—0074—06

2009—12—31

国家高技术研究发展计划（863计划）资助项目（2009AA11Z211）；国家自然科学基金资助项目（50875174）；上海市教育委员会重点学科建设项目（J50503）

（编辑 郭 伟）

孙首群，男，1964年生。上海理工大学机械工程学院副教授、博士。研究方向为机电系统的电热耦合效应及轴承转子系统动力学。赵玉香，女，1980年生。上海理工大学机械工程学院硕士。徐 伟，男，1985年生。上海理工大学机械工程学院硕士研究生。杨 凡，男，1984年生。上海理工大学机械工程学院硕士。杨 炎，男，1986年生。上海理工大学机械工程学院硕士研究生。