德布罗意物质波和玻恩对波函数的统计解释

薛立范

包头轻工职业技术学院，内蒙古包头 014035

德布罗意在爱因斯坦的光子学说的启示下，通过对几何光学和经典力学的对比，大胆的提出了物质波的假设，促进了物理学的发展。

1 德布罗意物质波假设

20世纪20年代前后，有关原子结构和量子理论的研究引起了当时很多物理学家的关注。爱因斯坦的光量子理论通过密立根、康普顿等人的研究得到了证实，德布罗意对此发生了很大的兴趣，他认为在对光的研究过程中，同时引进了粒子概念和周期性概念，光本身必须同时考虑粒子性和波动性。他进一步研究了几何光学和经典力学的对应性，几何光学中的费马原理和经典力学中的莫培丢变分原似，他大胆设想，不仅光具有粒子性和波动性两种性质，而且一般的物质也具有这两种性质。德布罗意认为：既然粒子概念在波的领域里成功的解释了令人困惑的光电效应，那么，波动概念也应该能解释在粒子领域中令人困惑的定态问题。

1923年～1924年期间，德布罗意陆续发表了《波和粒子》、《光量子，衍射和干涉》等论文，提出了物质波的概念，他认为一个能量为E ，动量为P 的粒子与频率为γ，波长为λ的波相对应。仿照爱因斯坦关系，粒子的能量、动量与相应的频率、波长之间的关系为：

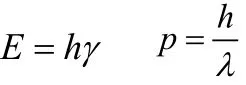
这个关系我们称之为德布罗意关系。

在此基础上，他用物质波概念分析了玻尔量子化条件的物理基础。氢原子中电子波绕原子核的圆周轨道传播一周后应光滑的连接在一起，否则将会由于干涉相互抵消，不能形成稳定轨道。这就要求轨道的周长应是波长的整数倍，即满足：

式中r是电子绕核的轨道半径，λ是电子波的波长。利用德布罗意关系，可以得出玻尔量子化条件：

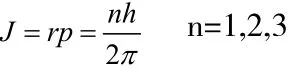
德布罗意的物质波假设在当时并没有引起很大的注意，原因为：

首先，这个假设只是对玻尔的量子化条件提供了一个解释方案，并没有得出新的结论。其次，这种物质波究竟是什么东西，并不明确，在试验上也没有证实。最后，由于经典物理学的传统概念，对粒子看作既是粒子又是波的观念太超乎一般人的认识。

后来，德布罗意的导师朗之万将他的论文推荐给爱因斯坦并得到了爱因斯坦的高度赞扬，这才引起人们的重视。薛定谔正是在爱因斯坦的建议下，对德布罗意的假说进行了仔细的研究，导致了波动力学的诞生。

1927年美国物理学家戴维逊和革莫用电子的衍射实验证实了电子波的存在，而且也证实了德布罗意关系，德布罗意物质波的假设得到了实验的证实。

2 玻恩对波函数的统计解释

按照德布罗意物质波假设，一个能量为E ，动量为P 的粒子与频率为，波长为λ的波相对应，在三维空间中，可以用样一个平面波来代表它。C是常数，ψ(r, t)称为波函数，那波函数又有什么物理意义呢。

起初，一些物理学家仍按照经典物理中的粒子和波相对立的观点，总想将一个寓于另一个之中，或认为粒子性比波动性更基本，或认为波动性比粒子性更重要，但这些解释都不能符合众多的实验事实。1927年，德国理论物理学家玻恩给出了波函数的统计解释：波函数在空间某一点的强度即振幅绝对值的平方和在该点发现粒子的几率成正比。

在证明电子具有波动性的衍射实验中，当电子通过晶体衍射打到屏上时，出现明暗相间的衍射圆环，衍射环的明暗程度代表了到达那里的德布罗意波ψ的强度的大小。最亮的地方表示最大，最黑的地方表示=0。

当减小电子流的强度，以致电子可以一个一个的到达屏上时，在屏上出现的图样则变成完全是毫无规则的，只有当时间足够长以后，有众多的电子到达屏上之后，屏上才出现明暗相间的衍射条纹。这说明所描述的粒子遵循着满足统计规律的运动。玻恩正是利用电子衍射实验中出现的这样特殊的规律，提出了他对波函数的统计解释：波函数在空间某一点的强度（振幅绝对值的平方）和在该点发现粒子的几率成正比。按照这个解释，物质波又可以叫做几率波。

按照波函数的统计解释，波函数告诉了我们粒子在某处出现的几率是多少，在另一处出现的几率又是多少等等。当然这也是对粒子运动状态的一种描述，因此量子力学中，对一个系统状态的描述与经典力学中完全不同。在经典力学中，一个质点的运动状态可以用它的位置和动量来确定，运动状态随时间的变化规律可以由牛顿定律来决定，即经典力学对质点的运动状态给出了决定性的预言。但是在量子力学中，由波函数的统计解释可知，对粒子运动状态的描述是几率性的，它不能告诉我们粒子到底在什么位置，只能告诉我们粒子处于某处的几率大小。当系统由一种状态变化为另一种状态时，我们得到的仍然是系统状态的几率性描述。因此，量子力学中对粒子运动的描述没有确定的轨道概念，我们对粒子运动状态的演化只能给出几率性预言，而不是决定性预言。造成这种现象的根本原因就是波粒二象性。

但是，量子力学中的几率波和经典波是完全不同的。首先，经典波，例如声波、水波等代表了某种介质中振动的传播过程，而几率波不代表任何介质振动，其次，经典波的振幅本身大小有绝对意义，它的平方和振动能量成正比，而几率波振幅绝对值的平方表示该点发现粒子的几率，同时由于波函数可以归一化，所以几率波的振幅却可以任意乘以一个常数，但它们代表得却是相同的物理状态。

[1]屠庆铭.大学物理[M].北京：高等教育出版社，2009.

[2]陈信义.大学物理[M].北京：清华大学出版社，2008.

[3]宋峰.大学物理学基础教程(下)[M].北京：高等教育出版社，2008.