GOCE卫星径向重力梯度一阶、二阶径向偏导数标准差的近似解析公式
徐天河,贺凯飞
1.武汉大学测绘学院,湖北武汉430079;2.西安测绘研究所,陕西西安710054;3.长安大学地测学院,陕西西安710054
1 引 言
欧洲地球重力场和海洋环流探测卫星(GOCE)重力场恢复涉及诸多研究内容,如数据预处理、数字滤波、大型方程组快速解算、正则化算法等[1-3],而重力梯度数据预处理是其中的关键问题,主要包括数据的粗差探测、系统误差标定、数据归算等[1-2]。系统误差标定经常涉及重力梯度数据的延拓处理,如卫星轨迹交叉点不符值计算中的延拓。此外,空域法恢复GOCE重力场中,需要将卫星重力梯度观测值延拓到平均轨道面,同样涉及梯度数据的延拓处理[4-8]。许多学者对卫星重力梯度的延拓进行深入研究,并使其在GOCE数据质量评定、系统误差标定、GOCE重力场恢复中得到广泛应用[9-15]。也有部分学者对GOCE卫星重力梯度(satellite gravity gradient,SGG)延拓误差的量级进行估计,但大都集中在数值分析上,且主要考虑重力场模型、坐标转换等带来的误差影响,而利用解析方法研究GOCE卫星SGG数据的延拓误差及可忽略的延拓误差最大高度方面研究较少[6,9]。实际上,在一定的延拓高度范围内,延拓误差可以忽略,即可用观测点梯度值代替延拓点梯度值[1,13]。若能从解析角度分析延拓的误差影响,并较准确估计可忽略的延拓误差最大高度,不仅能大大简化计算,也可为GOCE数据处理提供有益参考。要对此进行解析估算,涉及的关键问题是重力梯度一阶、二阶径向偏导数的方差或标准差解析公式的推导。考虑到径向重力梯度Tzz是GOCE卫星重力梯度最主要的观测分量以及论文篇幅的限制,以Tzz为例,立足于推导GOCE卫星Tzz的一阶、二阶径向偏导数˙Tzz、¨Tzz标准差的近似解析公式,试图给出简便、快捷的计算公式及量级估计,由此给出实际延拓计算中可忽略的延拓误差最大高度。因此,本文推导出的近似解析公式具有理论和实践意义。
2 径向重力梯度Tzz的延拓公式及误差分析
卫星的扰动位公式可表示如下[16-17]

式中,φ和λ为空间单位质点在地固系中的纬度和经度;r为卫星的地心距;Re为地球平均半径;GM为地球引力系数为正常化的缔合勒让德尔多项式;Cnm和Snm为正常化的地球引力位系数;l和m为多项式的阶和次。
由式(1)对r求二阶导数便可得出径向重力梯度Tzz的计算公式[16-17]

在GOCE数据预处理如利用卫星交叉点不符值,以及利用空域法进行GOCE重力场恢复的计算中,通常要进行卫星重力梯度的延拓处理。GOCE卫星径向重力梯度的延拓公式可近似采用如下泰勒级数展开的形式(忽略二阶以上展开项)[6]

考虑到延拓高度是小量(相对于卫星高度),实际中可以忽略二阶以上的误差影响[6]。不考虑一阶项和二阶项的相关性,由误差传播定律,有如下公式
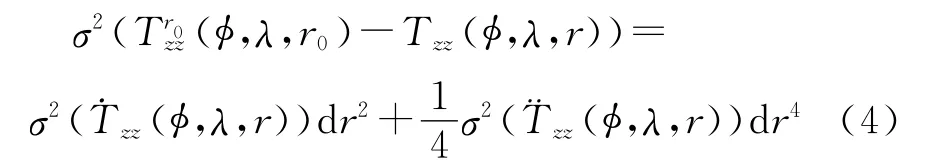
可忽略的延拓误差最大高度应满足如下条件

式中,σobs为观测值的标准差,利用式(4)、(5)进行可忽略延拓误差的最大高度的判别时,需要计算卫星径向重力梯度的一阶、二阶径向偏导数的标准差,因此主要目标便是推导其解析表达式。
3 Tzz一阶、二阶径向偏导数标准差的近似解析表达式及数值分析


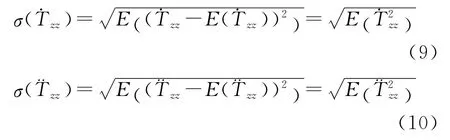
依据球谐分析公式[18]

根据Kaula准则[18]

由此可得

同样可推出

考虑到

式中,ki、kj的值见表1、表2。
令e-α=ρ2,即α=-2lnρ,由此可将公式(13)、(14)改写为
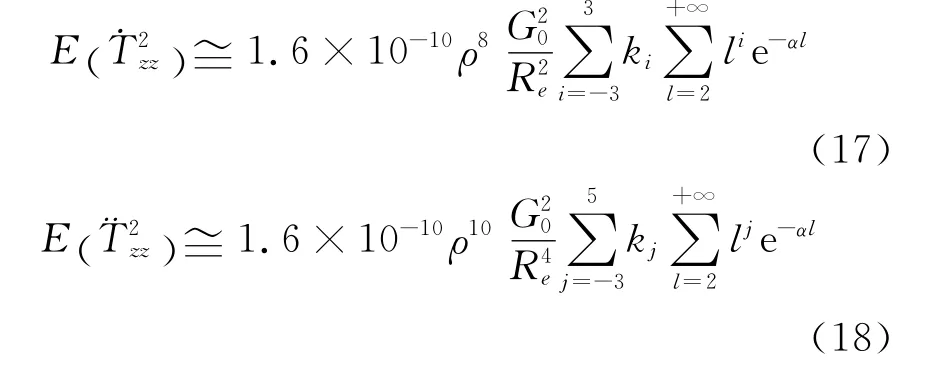
考虑到

并顾及[19]

式中,Γ为伽玛函数,则有


取GM=398 600.441 5×109,Re=6 378km,GOCE卫星轨道高度取为h=250km,即r≅Re+h=6 628km,由此计算得到ρ≅0.962 281,α=0.076 895,G0=1.536 2×10-6s-2,Γ(i+1,2α)、Γ(j+1,2α)可依据数学库函数计算得到,具体见表1、表2。由此得到GOCE卫星σ()和σ()的近似估值为
表1 计算公式中的系数ki及对应Γ函数值Tab.1 The values of kiandΓfunction ofσ
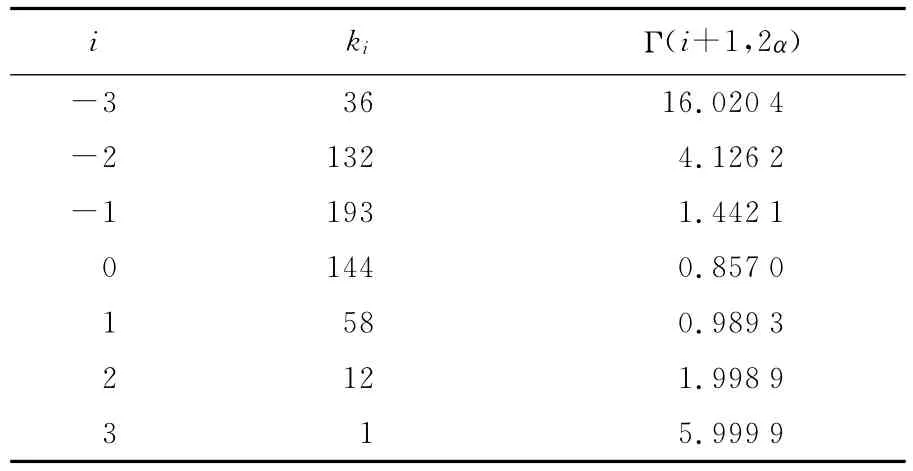
表1 计算公式中的系数ki及对应Γ函数值Tab.1 The values of kiandΓfunction ofσ
i ki Γ(i+1,2α)-3 36 16.020 4-2 132 4.126 2-1 193 1.442 1
表2 计算公式中的系数kj及对应Γ函数值Tab.2 The values of kjandΓfunction ofσ
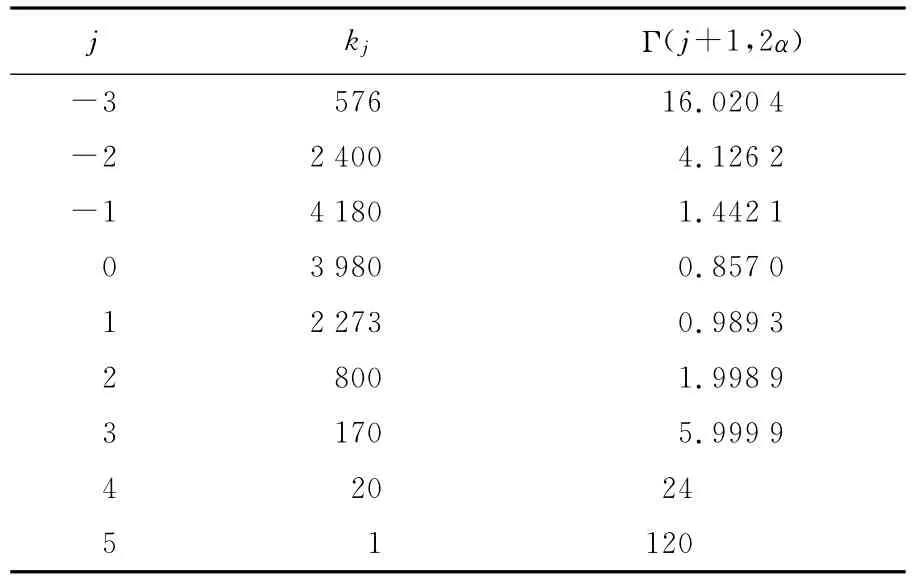
表2 计算公式中的系数kj及对应Γ函数值Tab.2 The values of kjandΓfunction ofσ
j kj Γ(j+1,2α)-3 576 16.020 4-2 2 400 4.126 2-
实际的重力场模型阶数只能截断到一定阶次如360,假定重力场模型最大阶数为Nmax,则式(22)、(23)可改写为
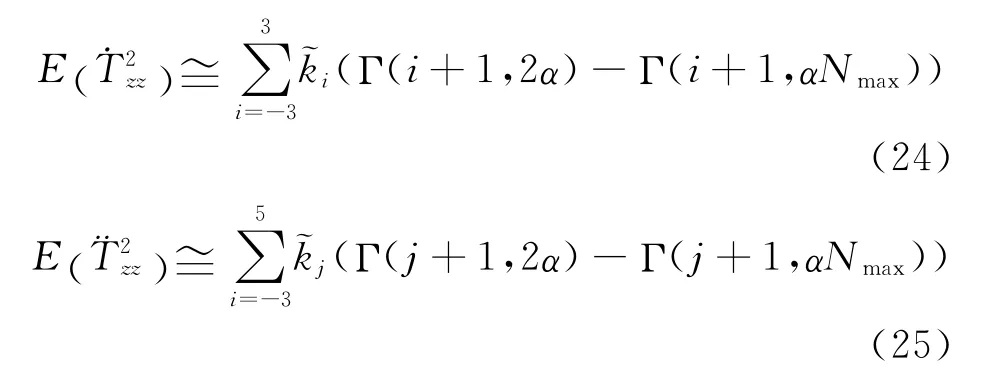
显然当阶数超过一定范围时(如图1中180阶以上、图2中200阶以上)几乎不发生变化,这从另一方面说明,在利用现有重力场模型对梯度数据进行延拓时,重力场的阶数取200阶以上即可。

图1 随Nmax变化的计算结果Fig.1 The values ofwith different Nmax
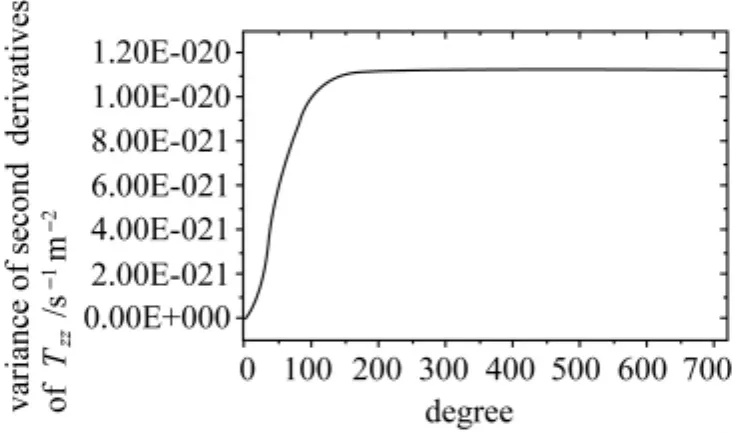
图2 随Nmax变化的计算结果Fig.2 The values ofwith different Nmax
4 Tzz平均轨道面延拓计算中可忽略的延拓误差最大高度
轨道高度差异最大值可表示为Δhmax=2rsine,由于GOCE卫星偏心率e<0.001,由此Δhmax≈2re=13.3km,而空域法重力场恢复延拓中通常是取平均轨道作为参考面,因此平均延拓的最大高度
依据上一节解析公式的计算结果,若要满足1mE(1mE=10-12s-2)的延拓精度要求,对于而言可忽略的延拓误差最大高度约0.8km,而对而言约为13.4km。
显然,如果以GOCE卫星平均轨道面为基准面,实际延拓处理中可忽略二阶以上的高阶项影响,即用泰勒展开一阶即可满足精度要求,即

而对小于0.8km的延拓高度可忽略不计,可不作延拓处理。
5 计算验证
为了验证本文解析公式的正确性,模拟10d的GOCE卫星Tzz数据,采样间隔为5s,卫星高度约为250km,重力场采用EGM96模型截至200阶。采用严格公式(7)、(8)计算结果见图3、4,然后统计其标准差的计算公式见式的计算公式与之类似。将上述计算结果作为“真值”,将解析公式计算出的标准差与“真值”进行比较,结果见表3。


表3 解析结果与严格公式计算结果比较Tab.3 The comparison between analytical formula and strict formula

图3 公式(7)计算出的˙Tzz结果Fig.3 The results of˙Tzzfrom formula(7)

图4 公式(8)计算出的¨Tzz结果Fig.4 The results of¨Tzzfrom formula(8)
6 结束语
GOCE数据预处理及重力场恢复中经常涉及重力梯度数据的延拓,利用卫星重力梯度一阶、二阶径向偏导数的标准差信息能对可忽略的延拓误差最大高度进行估算和判别,以此确定延拓处理的必要性。从解析角度出发,推导出径向重力梯度Tzz一阶、二阶径向偏导数标准差的近似解析计算公式,由此对GOCE卫星Tzz可忽略的延拓误差最大高度进行估算,并利用严格公式的计算结果对近似解析表达式的正确性进行验证,结果表明,解析公式形式简单,其计算结果与实际结果吻合较好。本文的所推导出的解析公式可较容易推广到Tzz的N阶径向偏导数标准差的计算情形。
[1] ALBERTELLA A,MIGLIACCIO F,SANSO F.From Eötvös to mGal[R].Noordwijk:ESA/ESTEC,2000.
[2] XU Tianhe,HE Kaifei.Outlier Snooping Based on the Test Statistic of Moving Windows and Its Applications in GOCE Data Preprocessing[J].Acta Geodaetica et Cartographica Sinica,2009,38(5):391-396.(徐天河,贺凯飞.移动开窗检验法及其在GOCE数据粗差探测中的应用[J].测绘学报,2009,38(5):391-396.)
[3] XU Xinyu,LI Jiancheng,WANG Zhengtao,et al.The Simulation Research on the Tikhonov Regularization Applied in Gravity Field Determination of GOCE Satellite Mission[J].Acta Geodaetica et Cartographica Sinica,2010,39(5):465-470.(徐新禹,李建成,王正涛,等.Tikhonov正则化方法在GOCE重力场求解中的模拟研究[J].测绘学报,2010,39(5):465-470.)
[4] WU Xing,ZHANG Chuanding,ZHAO Dongming.Generalized Torus Harmonic Analysis of Satellite Gravity Gradients Component[J].Acta Geodaetica et Cartographica Sinica,2009,38(2):471-477.(吴星,张传定,赵东明.卫星重力梯度分量的广义轮胎调和分析 [J].测绘学报,2009,38(2):101-107.)
[5] WU Xing,ZHANG Chuanding,LIU Xiaogang.Leastsquares Harmonic Analysis of Radial Satellite Gravity Gradients[J].Acta Geodaetica et Cartographica Sinica,2010,39(5):471-477.(吴星,张传定,刘晓刚.卫星重力径向梯度数据的最小二乘配置调和分析 [J].测绘学报,2010,39(5):471-477.)
[6] TOTH G,FOLDVARY L.Effect of Geopotential Model Errors on the Projection of GOCE Gradiometer Observables[C]∥Gravity,Geoid and Space Missions,IAG International Symposium.Portugal:IAG,2004.
[7] JARECKI F,WOLF K I,DENKER H,et al.Observation of the Earth System from Space[M].Berlin:Springer,2006:271-285.
[8] MÜLLER J,JARECKI F,WOLF K I.External Calibration and Validation of GOCE Gradients[C]∥Gravity and Geoid 2002 3rd Meeting of the International Gravity and Geoid Commission.Thessaloniki:Ziti Editions,2003:268-274.
[9] MULLER J.GOCE Gradients in Various Reference Frame and Their Accuracies[J].Advances in Geosciences,2003(1):33-38.
[10] JARECKI F,MULLER J.Validation of GOCE Gradients Using Crossovers,in Geotechnologien:Observation of the System Earth from Space[R].Karlsruhe:Geotechnologien,2003.
[11] JARECKI F,MULLER J.GOCE Gradiometer Validation in Satellite Track Cross-overs[C]∥Proceeding of the 1st International Symposium of the International Gravity Field Service.Istanbul:International Association of Geodesy,2006.
[12] JARECKI F,MULLER J.Robust Trend Estimation from GOCE SGG Satellite Track Cross-over Differences[C]∥Observing Our Changing Earth,International Association of Geodesy Symposia.Perugia:International Association of Geodesy,2009:363-369.
[13] YANG Xue.GOCE Sensitivity Studies in Terms of Crossover Analysis[D].Stuttgart:University of Stuttgart,2009.
[14] MIGLIACCIO F,REFUNZZONI M,SANSO F,et al.The Latest Test of the Space-wise Approach for GOCE Data Analysis[C]∥Proceedings of the 3rd International GOCE User Workshop.Frascati:ESRIN,2007:241-247.
[15] ARABELOS D,TSCHERNING C C.On a Strategy for the Use of GOCE Gradiometer Data for the Development of a Geopotential Model by LSC[C]∥Proceedings of the 3rd International GOCE User Workshop.Frascati:ESRIN,2007:69-75.
[16] RUMMEL R,KOOP M,KOOP R,et al.Spherical Harmonic Analysis of Satellite Gradiometry[M].Delft:Netherlands Geodetic Commission,1993.
[17] KOOP R.Global Gravity Field Modelling Using Satellite Gravity Gradiometry[M].Delft:Netherlands Geodetic Commission,1993.
[18] KAULA W M.Theory of Satellite Geodesy[M].Waltham:Blaisdell Publishing Company,1966.
[19] Writing Group of Mathematical Manual.Mathematical Manual[M].Beijing:Press of Higher Education,2004.(数学手册编写组.数学手册[M].北京:高等教育出版社,2004.)

