新型无轴承无刷直流电动机的结构设计与有限元分析

李兵伟，刘贤兴，许 洁

(江苏大学，江苏镇江212013)

0 引 言

无刷直流电动机是一种性能优越、应用前景广阔的电机，它结合了直流电机和交流电机的特点，既具备交流电机的结构简单、运行可靠、维护方便等一系列优点，又具备直流电机的运行效率高、无励磁损耗以及调速性能好等诸多特点［1］。

本文将磁悬浮技术应用于无刷直流电动机构造了一种两自由度的无轴承无刷直流电动机。这种电机具有无摩擦、无磨损、无污染、不需润滑和密封、高速度、高精度、高功率密度、寿命长等优点［2］，其转速可达5 000～80 000 r/min，且寿命可达上万小时，其紧凑的结构为研究特种新型电气传动系统提供了设计空间。因此，无轴承无刷直流电动机在数控机床、计算机外设、飞轮储能、医疗器械、航空航天等领域具有广阔的应用前景［3－4］。

电磁设计是高性能的无轴承无刷直流电动机的关键技术之一，本文对无轴承无刷直流电动机结构和运行规律进行了分析与研究，采用Ansoft/Maxwell 2D有限元分析软件［5］对无轴承无刷直流电动机进行了有限元分析，通过分析检验设计的正确性与合理性，为进一步优化无轴承无刷直流电动机的结构和参数做好准备。

1 二自由度无轴承无刷直流电动机结构设计及运行机理分析

1.1 无轴承无刷直流电动机结构设计与绕组排布

二自由度无轴承无刷直流电动机如图1所示，它采用两套绕组叠绕在同一定子槽中，一套为转矩绕组，用来产生电机转矩;另一套为悬浮力绕组，用来控制转子的径向位置。所采用的电机是12槽8极内转子无刷直流电动机。根据无轴承无刷直流电动机的悬浮和控制机理，我们对电机绕组结构和参数进行设计，具体结果如图2所示。

图1 二自由度无轴承无刷直流电动机基本结构

图2 无轴承无刷直流电动机绕组结构

转子起始位置如图2所示，第一块永磁体贴片充磁方向为由内向外，转子逆时针方向旋转，取第一块永磁体贴片下边缘与x轴间的夹角为转子位置角φ。其中 a11、a12、a111、a122 属于 a1绕组，a21、a22、a211、a222属于 a2绕组，a1与 a2属于 a套绕组，两分支相互独立，但a1a2各自包含的两组绕组是串联的。b和c套绕组也有类似的结构。在电机剖面图上⊗表示流入平面，⊙表示流出平面，并且在Maxwell 2D仿真规则中规定，电流流出平面赋正值，流入平面赋负值。

1.2 绕组导通规律分析

为了证明提出的绕组结构能够产生转子稳定悬浮所需的悬浮力，本文在假设要产生X轴正方向悬浮力的前提下，预估出所需要的绕组导通规律(详细推理过程限于篇幅不再展开)(如图3所示)，并运用有限元分析软件建立仿真模型，按照预期规律在不同的转子位置时刻加载相应的电流，由仿真结果可知，此种结构可以产生假定情况下预期的悬浮力，从而使电机转子在任何运行情况下的稳定悬浮成为可能。

图3中给出了转矩绕组U、V、W和悬浮绕组绕组A、B、C的电流在一个周期内的导通情况，图中纵坐标为电流值，横坐标为转子机械角。预期根据上述规律可生成x轴正方向的悬浮力。其中，悬浮绕组:a1=C A，a2=0 A，b1=0.5C A，b2=0.866C A，c1=0.866C A，c2=0.5C A，C 是一个常量。

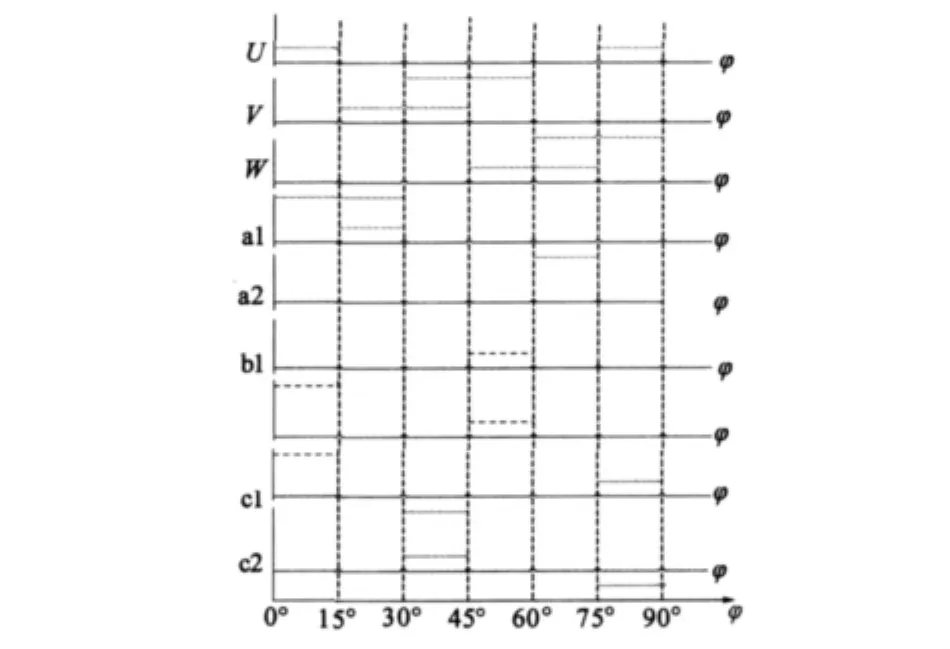
图3 绕组导通规律

电机为8极，故电机一对磁极对应360°电角度，其对应的机械角度为90°，又由于电机为12槽，槽间夹角为30°，据绕组形式可知，电机运行以90°机械角为周期。转矩绕组与传统无刷直流电动机的导通规律类似，工作于两相导通三相星型六状态下，每刻均有两相绕组导通，各相绕组分别持续导通120°电角度。

1.3 悬浮力产生原理及数学模型［6－7］

在图4中，根据绕组排布规律，为三套悬浮力绕组a、b、c定义了三个坐标平面，其中a1－a2面与x－y坐标面重合，b1－b2、c1－c2坐标面分别由a1－a2坐标面逆时针方向旋转120°和 240°获得。

根据图3，将一个周期分为6段，每段跨越15°机械角，下面阐述这六个空间段内悬浮力的生成方式与其所遵循的数学公式。

图4 坐标定义

在0°～15°与 45°～60°阶段，b套悬浮绕组导通，由b1与b2产生的电磁力依据矢量合成来生成x轴正向的悬浮力，如图5所示。

图5 0°～15°与45°～60°阶段转子受力矢量合成图

所产生悬浮力的大小与悬浮绕组中加载的电流大小有关，并且两个并联分支中电流的比例决定产生力的方向，大小决定力的大小。根据对三套悬浮绕组坐标面的定义，可以将其产生悬浮力的大小转化为常用的x－y正交坐标系下的量来分析，结果如下:

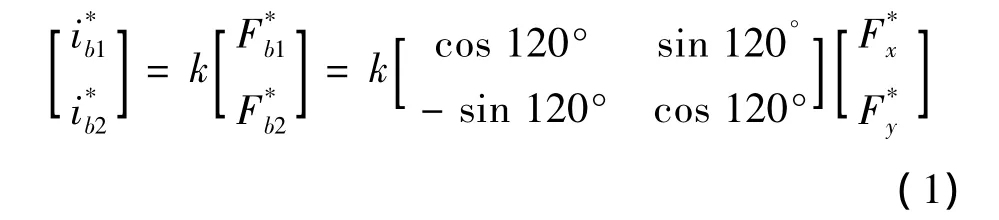
式中:k为比例系数，以下两式同理。

在15°～30°与 60°～75°阶段，a 套悬浮绕组导通，由a1与a2产生的电磁力依据矢量合成来生成x轴正向的悬浮力，与另两组不同之处在于，这两个空间段每次只导通两个分支中的一支来产生x轴正向的悬浮力，如图6所示。

图6 15°～30°与60°～75°阶段转子受力矢量合成图

所产生悬浮力的大小与悬浮绕组中加载的电流关系:

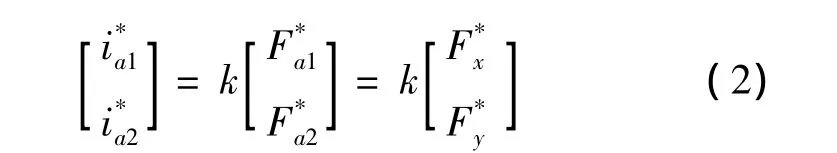
在30°～45°与 75°～90°阶段，c套悬浮绕组导通，由c1与c2产生的电磁力依据矢量合成来生成x轴正向的悬浮力，如图7所示。

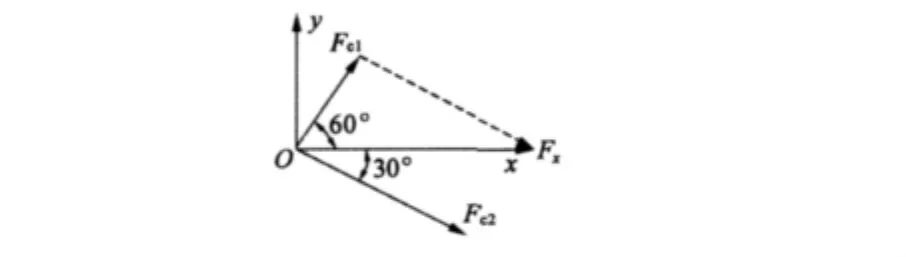
图7 30°～45°与75°～90°阶段转子受力矢量合成图

所产生悬浮力的大小与悬浮绕组中加载的电流关系:

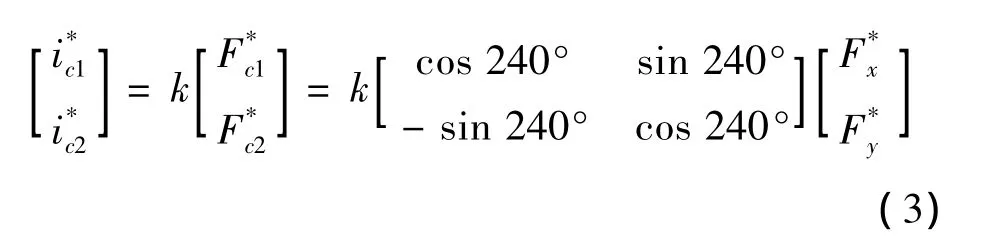
2 二自由度无轴承无刷直流电动机的有限元分析

采用Ansoft/Maxwell有限元分析软件对无轴承无刷直流电动机进行有限元分析，根据无轴承无刷直流电动机绕组导通规律，由Maxwell 2D静磁场分析［8］结果可知，该无轴承电机绕组结构可以产生指定方向的稳定悬浮力，可以实现两自由度的稳定运行，满足设计要求。磁路分析如图8所示。

图8 二自由度无轴承无刷直流电动机的磁路分析

图中，T1～T6分别对应上节所述的一个导通周期中的六个空间段。为了克服永磁磁场的强大影响，得到明显的效果图，磁感应强度矢量分布图是在加载较大电流情况下得到的，但其只是为了使试验效果明显，以便于分析比较，仍具备参考价值。

现对仿真结果做以下分析:

(1)磁感应强度矢量分布图

从磁感应强度矢量分布图中可以看出磁场的强度分布与方向走势。例如，在T1与T3中，b绕组导通，从图中可知b1绕组所对应的两个定子齿处一个磁场变弱，另一个磁场变强。对于b2绕组也是如此。根据麦克斯韦力的产生原理可知，会产生如图4中与方向的麦克斯韦力，其大小取决于电流的大小，而这两个力的方向与x轴正方向夹角分别为60°与30°，只要两者的比例满足要求其合力就可以满足设计要求指向x轴正方向。

同理T2与T4、T3与T6分别与图5、图6对应，可以做同上的分析结果。

可知，仿真结果与理论分析基本一致。

(2)转子受力波形

转子受力波形图中横坐标为有限元分析的求解次数，纵坐标为转子受到的悬浮力，单位为N。从图中可见，转子在各指定位置处受力变化趋势是逐步趋于稳定的。而受力大小可以通过调节给定电流来调节。另外，波形中的震荡反映了一些干扰因素，主要有以下两方面:

(a)悬浮绕组与转矩绕组间的耦合与相互干扰。

由于本文阐述的绕组结构使同齿的悬浮绕组和转矩绕组不同时导通，从而降低了干扰。

(b)转子上的永磁体在悬浮绕组中感生EMF。

本结构中悬浮绕组的排布是对称的，且关于转轴对称的两分支是相互串联的，所以，每套悬浮绕组的各分支中感生的EMF大小相等、方向相反，基本相互抵消。

通过以上分析，证明了本设计可以有效地降低干扰，而且可以产生大小与方向可调的悬浮力，在此基础上，只要采用适当的控制方法就可以在各个转子位置时刻通过实时跟踪调节来产生使转子趋于稳定的悬浮力，因此此设计是可行的。

3 无轴承无刷直流电动机优化后的主要参数

无轴承无刷直流电动机模型的主要参数如表1、表2所示。

表1 无轴承无刷直流电动机定转子参数

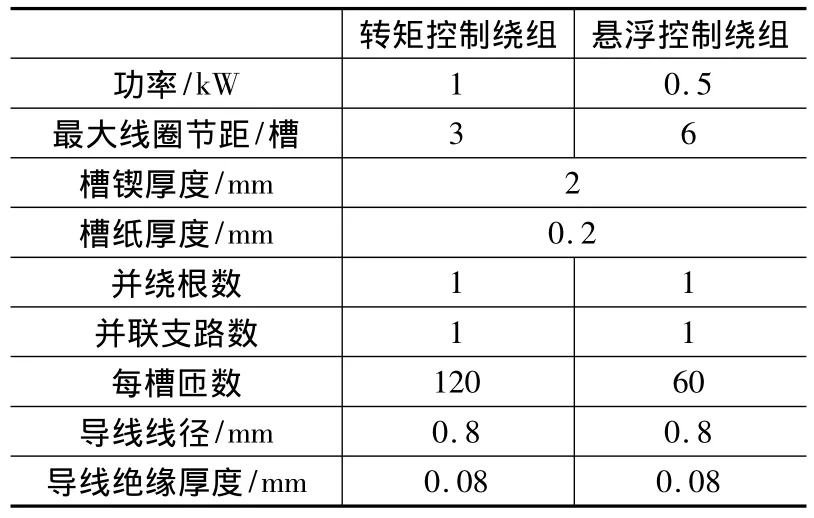
表2 无轴承无刷直流电动机绕组参数

4 结 语

本文将磁悬浮技术应用于无刷直流电动机，构造了一种两自由度的无轴承无刷直流电动机，提出一种新型的绕组结构。设计了原型机，并根据磁悬浮力产生机理估算出针对产生X轴正方向悬浮力时一个周期内的绕组导通规律，并应用Maxwell 2D软件建立2D仿真模型，进行静磁场分析。通过对仿真结果的分析，说明在预估的绕组导通规律下可产生基本稳定的X轴正向悬浮力，并且此力的大小与方向均可调，这就为实现转子的稳定悬浮控制奠定了基础。这就说明了所提出的新型电机绕组分布及结构的合理性，也说明本设计是可行的。

后期实验后，可以继续对电机的结构参数进一步优化，改善电机的运行性能，尤其是对转矩脉动与转子稳定悬浮要进行更深入的研究。

［1］孙建忠，白凤仙.特种电机及其控制［M］.北京:中国水利水电出版社，2005.

［2］贾磊.无轴承无刷直流电机原理与控制技术［D］.江苏大学，2009.

［3］方晓厅.磁悬浮无刷直流电机及其在计算机硬盘中的应用研究［D］.西北工业大学，2006.

［4］方晓厅，卢建康，高扬，等.磁悬浮无轴承无刷直流电动机控制及仿真研究［J］.微电机，2006，39(1):66－68.

［5］费德成，孙玉坤，朱幌秋.Ansoft软件在电机教学中的应用［J］.电气电子教学学报.2009，31(5):95－97.

［6］Ooshima M.Winding Arrangement to Increase Suspention Force in Bearingless Motors with Brushless DC Structure［C］//Proceedings of Industrial Electronics Society，2007.IECON 2007.33rd Annual Conference of the IEEE.TaiPei，2007:181－186.

［7］Ooshima M.Magnetic Suspension Characteristics of a Bearingless Brushless DC Motor［C］//Power and Energy Society General Meeting－Conversion and Delivery of Elecrical Energy in the 21st Century.Pittsburgh，USA，2008:1－5.

［8］刘国强.Ansoft工程电磁场有限元分析［M］.北京:电子工业出版社，2005.