虚拟装配中拆卸序列规划算法的研究与实现
米小珍 甄晓阳 周韶泽
大连交通大学,大连,116028
虚拟装配中拆卸序列规划算法的研究与实现
米小珍 甄晓阳 周韶泽
大连交通大学,大连,116028
为了解决装配体拆卸序列的生成与优化问题,利用零件的拆卸约束关系,建立了矩阵表达的包括几何约束、拆卸工具约束以及稳定性约束的多目标数学模型。利用干涉矩阵确定可行的拆卸方向,利用支撑矩阵分析拆卸过程的稳定性,利用拆卸工具列表分析拆卸过程中所用的拆卸工具。在运用蚁群算法寻求最优的拆卸序列过程中,加入方向变化因子、工具变化因子和稳定性因子,对拆卸转移概率公式进行了改进,通过更新局部和全局信息素,指导算法快速寻找最优解,最后以动车组转向架轮对作为实例验证了算法的可行性。
拆卸序列规划;干涉矩阵;支撑矩阵;蚁群算法
0 引言
装配/拆卸序列规划作为虚拟装配技术(VA)的重要组成部分,可在产品设计阶段实现装配体的预装配/拆卸,进而验证装配/拆卸工艺的正确性,为产品设计开发人员提供研究平台和手段。装配/拆卸序列规划实际上是一个组合优化问题,传统的优先约束关系法和图论中的割集理论都存在组合爆炸的弊端,对解决复杂装配体的序列规划效果欠佳。近年来许多学者开始采用基于智能计算的软计算方法来解决装配/拆卸序列规划问题,并取得了一定成果。目前,大多数学者采用的是遗传算法和蚁群算法(ant colony algorithm,ACO),遗传算法是一种基于自然选择和自然遗传学机制的搜索算法,能解决调度、过程规划、车间布局等组合优化问题,但也存在着收敛速度慢和所选参数影响大的缺点。文献[1-2]将遗传算法和蚁群算法进行了比较,实际应用表明蚁群算法在解决装配/拆卸序列规划问题上要优于遗传算法。
蚁群算法的基本思想是模仿蚂蚁依赖信息素(pherom one)进行通信而显示出它的群体本性,每只蚂蚁根据路径上的信息素强度进行选择,最终体现为整个蚁群寻找到最优路径。文献[3]首先将蚁群算法应用于装配/拆卸序列规划研究,但其算法没有涉及装配/拆卸序列的可行性。文献[4]从拆卸几何性出发,给出了解决装配/拆卸问题的蚁群算法,但假设装配体处于“失重”的情况下,没有考虑到装配体的拆卸稳定性。文献[5]将蚁群算法应用于产品拆卸序列规划,考虑了拆卸改变次数和拆卸零件总数原则。文献[6]将产品的拆卸序列规划问题描述为对该加权有向图中具备最优值的路径搜索和寻优问题,提出了一种蚁群优化算法。本文运用装配体的拆卸干涉矩阵来判断可行的拆卸方向,用支撑矩阵判断拆卸零件对装配体稳定性的影响,并加大稳定性在拆卸过程中的主导作用,对拆卸序列的生成及优化进行深入研究,使最终序列更加贴近工程实际。
本文按照“可拆即可装”的原则,运用蚁群算法研究装配体的完全拆卸序列规划,综合考虑了可行性、稳定性和装配或拆卸中所使用的工具等信息。
1 拆卸数学模型的建立
装配体拆卸模型提供了装配体和零部件的相关信息,是进行拆卸序列规划的基础。为了保证算法的有效性和实用性,要求所建立的拆卸模型既准确又不过于复杂。常用的拆卸信息表达模型可分为图模型和矩阵模型[1],图模型相对矩阵模型更加直观,图中的节点对应零件,边表示零件间的拆卸关系,但是图模型不易于计算机的表达和实现;矩阵模型可利用拆卸干涉矩阵描述零部件沿坐标轴拆卸时与其他零件的干涉情况,利用支撑矩阵描述某零件对其他零件的重力支撑情况,因而不仅可以较为完善地体现实际装配/拆卸工艺需求,而且易于算法的实现。本文采用矩阵方式对装配体进行建模,为蚁群算法进行拆卸序列规划提供必要信息。
1.1 拆卸可行性分析
一个几何可行的拆卸序列是指当沿着坐标轴拆卸零件时与其他未拆卸零件不发生干涉。装配体有n个零件的情况下,集成拆卸矩阵I D是一个n行、3n列的矩阵[7],它能完整描述拆卸过程中的干涉情况,其表达式如下:

集成矩阵I D中元素Iijx表示零件Pi不发生移动时,Pj沿+x方向拆卸时与零件Pi的干涉情况,如果Pj沿+x方向拆卸时与零件Pi发生干涉,那么定义Iijx=1;反之,则Iijx=0。零件Pj沿-x方向拆卸时与零件P i的干涉情况与Pi沿+x方向拆卸与零件Pj的干涉情况相同,由元素 Ijix表示。同样,可以确定集成干涉矩阵中其他元素的值。
零件Pj的可行拆卸方向是由未拆卸的m个零件决定的,当前待拆卸零件Pj的可行拆卸方向可用下式表示:

式(2)表示零件Pj沿d方向与未拆卸零件的干涉情况,假如Pj与所有未拆卸零件都没有干涉,即ψd=0,那么Pj沿着d方向是可以拆卸的,d方向为可拆卸方向,反之,不可拆卸。
1.2 拆卸稳定性分析
拆卸稳定性很大程度上决定了拆卸序列中零件的优先次序,传统的根据力和力矩平衡关系对装配体稳定性进行分析的方法,由于涉及大量数学计算,故效率较低。本文通过建立拆卸支撑矩阵[8]分析拆卸过程中装配体的稳定性,方法简单且实用性强,拆卸支撑矩阵S为
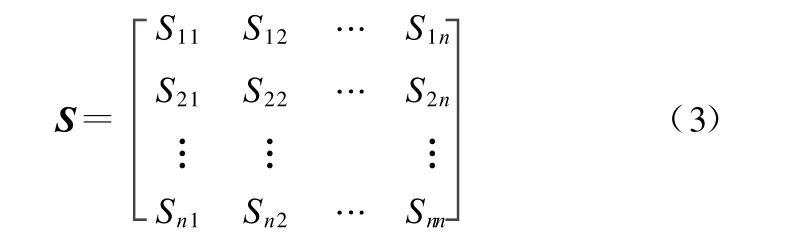
矩阵元素Sij表示零件Pi对零件P j的重力支撑关系,假如零件Pi对零件Pj有稳定支撑则定义Sij=1,零件Pi必须后于零件P j拆卸,反之,Sij=0,显然零件之间不接触时Sij=0。当前拆卸零件Pi对装配体的稳定性也是由未拆卸的m个零件决定的,可用下式进行分析:

当拆卸零件Pi时,需要判断零件Pi对所有未拆卸零件是否具有支撑作用,假如对其中任意的一个零件具有支撑作用,即Z>0时,不建议拆卸零件Pi;假如零件Pi对所有未拆卸零件都不具有支撑作用,即Z=0时,建议拆卸零件Pi。
2 基于蚁群算法的拆卸序列规划
实际拆卸序列的具体要求为:①拆卸可行且稳定;②拆卸方向变化最少;③使用工具变化最少;④拆卸难度小。本文以拆卸重定向次数和拆卸聚合性为标准,设置拆卸序列目标函数:

式中,Dn为拆卸方向改变次数(重定向性);Tn为拆卸工具更换次数(聚合性);w1、w2为二者的权重比系数。
运用蚁群算法进行拆卸序列规划时,可在拆卸转移概率中加入方向改变因子dij(t)、工具变化因子tij(t)和稳定性因子sij(t),引导蚂蚁向目标函数靠近。
2.1 拆卸转移概率的定义
采用P表示零件号、D表示该零件的可拆卸方向、T表示拆卸该零件所需要的工具,则可定义拆卸操作为(P,D,T)。对于每个蚂蚁个体下一步所选择的拆卸操作由拆卸转移概率确定,i操作与j操作间的拆卸转移概率由信息素因子和期望启发函数因子决定,定义如下:

式中,τij(t)为信息素因子,表示 t时刻拆卸操作i与拆卸操作j之间的信息素残余量;dij(t)为期望启发函数因子,表示t时刻从拆卸操作i到拆卸操作j的拆卸方向变化因子,如果方向发生改变,取(0,1]之间较小的数,反之,取该区间内较大的数;tij(t)为期望启发函数因子,表示t时刻从拆卸操作i到拆卸操作j的拆卸工具变化因子,如果工具发生改变,取(0,1]之间较小的数,反之,取该区间内较大的数;sij(t)为期望启发函数因子,表示t时刻待拆卸零件j对其余未拆卸零件的稳定性影响,如果能够稳定拆卸,取(0,10]之间较大的数,反之,取该区间内较小的数;α、β、μ、γ分别为τij(t)、dij(t)、tij(t)、sij(t)的权值,表示各个因子对转移概率的影响强弱,β、μ、γ反映了启发信息在蚂蚁选择路径中的受重视程度,其值越大,则该转移概率越接近贪心规则[9]。
两个不同的拆卸操作之间的信息素残留越大,启发函数的值越大,则拆卸转移概率也就越大,蚂蚁就更倾向于选择此路径。
2.2 信息素矩阵的更新
信息素矩阵的行和列代表拆卸操作,当装配体包含n个零件时,该矩阵为6n×6n。为了避免路径上残余信息素过多而淹没启发信息,使搜索陷入局部最优解,在每只蚂蚁走完一步,即完成一次拆卸操作、或者将装配体完成拆卸后,要对残留信息素进行更新处理,本文采用局部更新和全局更新两种方式。
(1)局部信息素更新。更新方式如下:
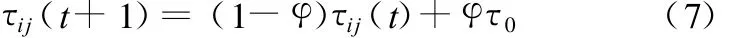
式中,τ0为初始信息素浓度;φ为局部信息素挥发系数,φ∈(0,1),随着φ值增大,算法收敛性速度变慢。
完成从拆卸操作i到拆卸操作j后,更新此路径上的信息素,能够有效避免优势路径上信息素过分积累,使整个蚁群对未选中的路径有较强的探索能力。
(2)全局信息素更新。更新方式如下:
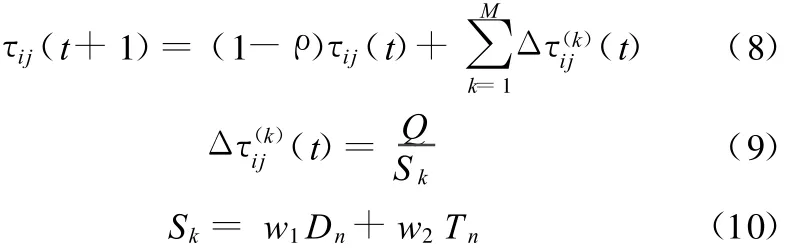
式中,ρ为全局信息素挥发系数,ρ∈(0,1);M为蚂蚁总数;Q为常数,用来调整信息素的增长量;Sk为解的质量,表示此条路径的好坏。
当蚂蚁完成一次周游后根据解的质量对此路径上的信息素进行更新。
2.3 算法步骤
拆卸序列规划流程如图1所示。

图1 基于蚁群算法的拆卸序列规划流程图
3 拆卸实例分析
图2为CRH 3动车组转向架轮对爆炸图,为简化计算,拆卸序列规划中把螺栓组作为单个零件来处理。轮对装配体零件数为21,各个零件所用拆卸工具如表1所示。
应用上述蚁群算法,参数选择如下:初始信息素浓度τ0=1,信息素权值α=0,方向变化因子权值β=2,工具变化因子权值γ=2,稳定性因子权值μ=3,信息素总量Q=10,蚂蚁个数M=6,循环次数Nc,max=200,选择零件11为基准件,算法在循环到第70次时获得如下近优/最优解:(7,-z,T6)→(6,-z,T6)→(17,-z,T6)→(16,+x,T6)→(15,+x,T3)→(14,+x,T4)→(21,+x,T1)→(19,+x,T2)→(20,+x,T2)→(18,+x,T2)→(13,+x,T3)→(5,-x,T3)→(8,-x,T4)→(1,-x,T1)→(2,-x,T2)→(4,-x,T2)→(3,-x,T2)→(9,-x,T3)→(10,-x,T4)→(12,-x,T4)→(11,-x,T5),最终序列的拆卸方向变化次数为2,拆卸工具变化次数为11,目标函数值 f=5.6,算法耗时1.078s。图3体现了循环次数与当前最优解之间的函数关系。

图2 CRH 3动车组转向架轮对爆炸图
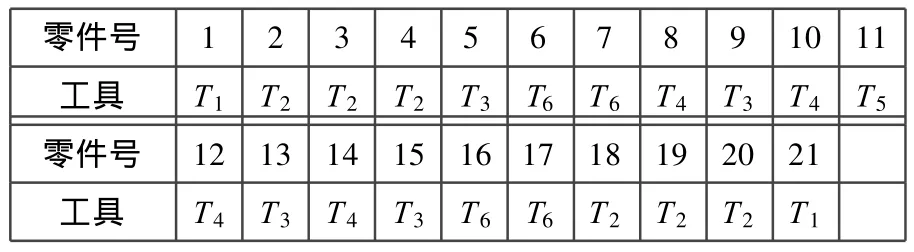
表1 各零件所用的拆卸工具

图3 循环次数与当前最优值关系
在搜索近优/最优解过程中,信息素在不断地发生变化,每一步寻优的过程就是在可行的拆卸操作中寻找信息素较大的两个拆卸操作。优化前,不同拆卸操作之间信息素量初始值τ0=1,蚂蚁选择各拆卸操作的几率相同。优化后,较优的拆卸操作之间信息素量增大(为使蚂蚁有探索新路径的能力,信息素量不大于7),较差的拆卸操作之间信息素量减少(选择最少的路径上信息素量接近0),从而引导蚂蚁在概率选择过程中寻找优化的拆卸路径。
4 结语
本文建立拆卸干涉矩阵和支撑矩阵来表达几何约束关系和稳定性约束关系,由此分析几何可行性和拆卸稳定性,通过改进的拆卸转移概率公式以及更新局部和全局信息素,在运用蚁群算法寻求最优的拆卸序列过程中指导算法快速寻找最优解。最后将算法成功应用于动车组转向架的虚拟装配/拆卸序列规划,实际应用表明该方法的效果良好。但是在零件数目较大的情况下,算法易出现陷入局部最优解,为了解决这个问题,将蚁群算法与其他智能算法的融合是一个可行的研究方向。另外,评价函数的准确建立、参数的搭配优化、子装配体的识别以及拆卸信息的自动获取方面还有很多的工作要做,这是下一步对该方法进行改进的重点。
[1] 宁黎华.面向装配序列规划的软计算方法研究[D].桂林:桂林电子科技大学,2006.
[2] 章小红.基于蚁群算法的产品拆卸序列规划方法研究[D].武汉:华中科技大学,2007.
[3] Failli F,DiniG.Ant Co lony Systems in Assemb ly Planning:a New A pp roach to Sequence Detec tion and Op tim ization[C]//Proceeding of the 2nd CIRP International Sem inar in Intelligent Computation in Manufac turing Engineering.Cap ri,2000:227-232.
[4] W ang JF,Liu JH,Zhong Y F.A Novel Ant Colony Algorithm for Assembly Sequence Planning[C]//Advanced Manufacturing Technology.London,2004:1137-1143.
[5] 王峻峰,李世琪,刘继红.面向绿色制造的产品选择拆卸技术研究[J].计算机集成制造系统,2007,13(6):1907-1102.
[6] 王辉,向东,段广洪.基于蚁群算法的产品拆卸序列规划研究[J].计算机集成制造系统,2006,12(9):1431-1437.
[7] 方建新.基于蚁群算法的装配序列规划研究[D].武汉:华中科技大学,2007.
[8] 管强,张申生,刘继红.装配过程稳定性分析[J].上海交通大学学报,2004,38(4):501-505.
[9] 段海滨.蚁群算法原理及其应用[M].北京:科学出版社,2005.
Research and Implementation of Disassembly Sequence Planning Algorithm in Virtual Assembly
Mi Xiaozhen Zhen Xiaoyang Zhou Shaoze
Dalian Jiaotong University,Dalian,116028
In order to solve the com binatorial optim ization problem of disassembly sequence planning,an ant colony algorithm-based approach was presented.A multi-objectivem athematicalmodelwasestablished w hich w asexpressed bymatrixes and contained geometric constraints,stability constraints and disassembly tool constraints.Interference matrix was used to analyze the feasible disassemb ly direction,support matrix was used to analyze the stability,and disassembly tool lists were used to analyze the tools used during operations.In order to find the optimal disassembly sequence more quickly,redirection factor,tool change factor and stability factor were added to the state-transition ru le.Local and g lobal pheromone were updated after operations so as to avoid a local op timal solution,to accumu late pheromone according to the quality of solutions and to guide ant co lony in searching the app roximate/optimal solutions quick ly.Finally,the disassem b ly sequence of CRH 3 bogie w heels was used as a case research to show the feasibility of the algorithm.
disassemb ly sequence p lanning;interferencematrix;supportm atrix;ant colony algorithm
TP391.9
1004—132X(2011)13—1576—04
2010—08—30
铁道部科技研究开发计划重点项目(2008J012-C);辽宁省教育厅科学技术研究计划高等学校创新团队项目(2008T18)
(编辑 郭 伟)
米小珍,女,1962年生。大连交通大学交通运输工程学院教授、博士研究生导师。主要研究方向为基于复杂装备的多学科协同设计、协同仿真、优化与集成管理、虚拟装配等。获国家科技进步二等奖1项、教育部科技进步二等奖 1项、大连市科技进步一等奖1项、中国航天工业总公司科技进步二等奖1项、实用新型专利1项。发表论文40篇。甄晓阳,男,1986年生。大连交通大学机械工程学院硕士研究生。周韶泽,男,1977年生。大连交通大学交通运输工程学院讲师。
