随机梁式结构特征值的子结构递推求解方法
万信华 黄 斌 高洪波
1.华中科技大学,武汉,430074 2.中铁第四勘察设计院集团有限公司,武汉,430063 3.武汉理工大学,武汉,430070 4.中交第二公路勘察设计研究院有限公司,武汉,430052
随机梁式结构特征值的子结构递推求解方法
万信华1,2黄 斌3高洪波4
1.华中科技大学,武汉,430074 2.中铁第四勘察设计院集团有限公司,武汉,430063 3.武汉理工大学,武汉,430070 4.中交第二公路勘察设计研究院有限公司,武汉,430052
将递推随机有限元法和子结构模态综合法结合起来,提出了求解随机梁式结构特征值的子结构递推求解方法。算例表明,对于较宽随机涨落范围内的随机特征值求解问题,子结构递推求解方法相对于传统的基于一阶、二阶泰勒展开的摄动随机方法而言,其结果能够更好地逼近蒙特卡罗模拟解。
随机梁式结构;子结构模态综合法;递推随机有限元方法;摄动
0 引言
在机械工程领域,存在大量的梁式结构(如起重机的悬吊臂)。如果将这些梁式结构的某些物理参数和几何参数视为随机量,那么可称这样的结构为随机梁式结构。20世纪70年代以来,人们针对随机结构的特征值求解等问题的研究取得了不同程度的进展[1-7]。
对于大型的确定性结构,如何获得其特征值的解是特征值问题研究的一个重要方向。其中,子结构方法是一种有效的数值方法[8]。文献[7]利用子结构模态综合法,并结合普通的摄动随机有限元法,研究了随机结构的特征值求解问题,然而由于该方法只采用了一阶摄动法,随机特征值的均值和方差只有零阶和一阶精度,而且结构参数中的随机量被限制为小量,因此,当结构随机参数的变异性较大时,采用该方法结果精度会受到影响。
本文将文献[9-10]提出的递推随机有限元法和子结构模态综合法结合起来,提出了求解梁式结构特征值问题的子结构递推求解方法。悬臂桁架梁的数值分析结果显示,在较宽随机涨落范围内,虽然只采用了前四阶展式求解随机梁式结构的特征值,相对于传统的采用一阶、二阶泰勒展开的摄动随机有限元法的子结构方法而言,所提方法的结果能更好地逼近蒙特卡罗模拟解。
1 确定的子结构模态综合法
将一个结构系统按特点分割为若干子结构,当子结构的刚度矩阵和质量矩阵按内部自由度和附加边界自由度分块表示时,可写为

其中,上标I和B分别表示内部自由度和附加边界自由度,自由度数分别为n I和n B。对于固定界面子结构,其主模态 Φ(k)=[φ1 φ2 … φk]可由下面方程求得

其中,Λ(k)为由λi组成的子结构的特征值对角矩阵,另外,式中子结构主模态已经过正则化处理,主模态矩阵 Φc为n I×n B阶矩阵,由下式定义:

2 结构随机量的表达
如果结构的参数被视为随机量,系统的特征值方程(式(8))中的广义质量矩阵和广义刚度矩阵也是随机的,于是式(8)就变为随机的特征值方程。为了求解随机特征值方程,下面首先给出已知和待求随机量的表达。
2.1 子结构中的随机参数
假设整个结构系统被分割为p个子结构,每个子结构最多含有m个随机变量,且子结构之间的随机变量相互独立,则整个系统最多可有l(m×p)个随机变量。为方便起见,这里仅假设梁系结构的抗弯刚度或弹性模量为空间随机场,那么对于第s个子结构,它的刚度矩阵可表示为

其中,K0为均值参数对应的n×n维确定性矩阵,K si为n×n维矩阵;ξsi为独立的随机变量。事实上,对于质量、几何尺寸乃至边界支撑弹簧刚度等参数也可以有类似的表达。
2.2 随机特征值的非正交多项式展式
如果采用通常的摄动随机有限元法,未知的随机特征值可表示为关于小变异随机变量的摄动展开或泰勒展开。根据文献[9-10],采用如下非正交多项式展式表示未知随机特征值:

这里,a0(x)、ai1(x)等为未知系数,非正交多项式基φn(◦)的前三阶量可以写为

这里的非正交是相对正交而言的,即不同的多项式基的乘积经加权求积分后不再等于零。
3 随机特征值的子结构递推求解方法
3.1 子结构广义质量矩阵和刚度矩阵的表示
利用递推随机有限元法求解每个形如式(2)的子结构随机方程[9-10],可得每个子结构的特征值矩阵和主模态矩阵:

需说明的是,当子结构中的随机变量完全相关时,矩阵 Φc可处理为确定性矩阵,否则,为随机性矩阵。
3.2 系统总体广义质量矩阵和刚度矩阵的表示
在整理出每个子结构的广义质量矩阵和刚度矩阵后,依照有限元“对号入座”的装配方法,根据非正交展式中的系数项的阶数进行合并,可以得到整个结构系统的广义质量矩阵和刚度矩阵非正交展式的系数项。这样,整个系统的广义质量矩阵可表示为
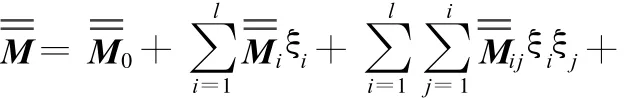

3.3 系统广义随机特征值问题
将式(16)及相应刚度矩阵代入特征值方程式(8)中,并将主特征值假设为如下非正交多项式展式:

依照上述方法,不仅可以推导出文献[7]中的一阶泰勒展开的摄动随机有限元子结构法,还可推导出二阶泰勒展开的摄动随机有限元子结构法。系统广义随机特征值的求解程序框图见图 1。

图1 系统广义随机特征值的求解程序框图
4 算例分析

图2 5跨悬臂桁架及其子结构分割
一个5跨悬臂桁架,其子结构分割形式如图2所示。悬臂桁架的水平和竖向杆件长为10m,斜杆长为14.14m,杆件截面积为1.0×10-4m2,密度为2800kg/m3。子结构1的杆件弹性模量为随机变量,均值为16GPa,变异系数为0.1。子结构2的杆件弹性模量均值为8.0GPa。两个子结构的动模态均取前5阶。

图3 三阶特征值均值和均方差与子结构2杆件弹性模量变异系数的关系(子结构1杆件弹性模量变异系数为0.1)
图3显示,在杆件弹性模量较大的随机涨落范围内,对于所求的振动特征值均值和均方差,四阶子结构递推求解方法比一阶、二阶摄动随机子结构方法都更逼近蒙特卡罗模拟解。在子结构2杆件弹性模量变异系数为0.28时,三阶特征值的一阶、二阶摄动随机子结构方法和四阶子结构递推求解方法与蒙特卡罗模拟解的误差分别为11.05%、8.62%和1.9%。和文献[10]类似,本文提出的子结构递推求解方法同样适用于梁单元结构,涉及更为复杂的结构单元时,采用所提方法还要具体区别对待、灵活处理。
5 结语
将递推随机有限元法和子结构综合模态法相结合,提出了求解随机梁式结构统计特征值的子结构递推求解方法。算例结果表明,和一阶、二阶摄动随机子结构方法相比,子结构递推求解方法能在较宽的随机涨落范围内更好地逼近蒙特卡罗模拟结果,即使仅采用四阶非正交多项式展式,逼近的效果仍是令人满意的。和蒙特卡罗方法相比,新的方法可以节省大量的计算时间;和直接的递推随机有限元法相比,本文方法能大量缩减结构自由度,对于大型复杂梁式结构而言,可以大大减小计算的规模。
[1] Hasselman T K,Gary C H.Modal Analysis o f Random Structural Systems[J].ASCE,1972,6(12):23-27.
[2] Fang Z.Dynam ic Analysis of Structures with Uncertain Parameters Using the T ransfer Matrix Method[J].Computers&Struc tures,1995,55(6):23-27.
[3] 朱位秋,吴伟强.基于随机场局部平均的随机有限元法[J].固体力学学报,1988,9(4):285-293.
[4] Prad lw arter H J,Schueller G I,Szekely G S,et al.Random Eigenvalue Problems for Large Systems[J].Computers and Structures,2002,80(27/30):2415-2424.
[5] Ghanem R,Spanos P.Polynom ia l Chaos in Stochastic Finite Elements[J].Journal of App lied Mechanics,1990,57:197-202.
[6] Xiu Dongbin,Em Karniadakia G.Modelling Uncertainty in Steady State Diffusion Prob lems via Generalized Polynom ial Chaos[J].Comput.Methods Appl.Mech.Engrg.,2002,191:4927-4948.
[7] 曹家玉,方之楚.工程结构的随机特征问题研究及其在梁结构中的应用[J].应用力学学报,2002,19(4):71-75.
[8] 楼梦麟.连接子结构与子结构模态综合法[J].振动工程学报,1995,8(1):52-56.
[9] 黄斌.一种新的谱随机有限元方法[J].武汉理工大学学报,2004,26(5):42-45.
[10] 黄斌,瞿伟廉.随机结构孤立特征值的统计特性[J].航空学报,2005,26(1):40-43.
Statistic Eigenvalue Analysis of Random Beam Structures Based on Substructure Recursive Approach
W an Xinhua1,2Huang Bin3Gao Hongbo4
1.Huazhong University of Science and Technology,Wuhan,430074 2.China Railway Siyuan Survey and Design Group Co.Ltd.,Wuhan,430063 3.Wuhan University of Technology,Wuhan,430070 4.China Communications Second Highway Survey Design and Research Institute Co.Ltd.,Wuhan,430052
A new numerical method,called as substructure recursive stochastic finite element method,which combined component modal synthesismethod w ith recursive stochastic finite element method,was em ployed to study eigenvalue problems of random beam structures.The numerical examp les of truss cantilever beam show that,com pared with perturbation stochastic substructure method based on the first or second order of Tay lor expansions,the results of the substructure recursive stochastic finite element method supposed herein are more close to that of Monte-Carlo simu lation method in w ide range of random fluctuation.
random beam structure;com ponentm odal synthesismethod;recursive stochastic finite elementmethod;perturbation
O326;TU31
1004—132X(2011)12—1476—04
2011—03—21
国家自然科学基金资助项目(51078297)
(编辑 王艳丽)
万信华,男,1968年生。华中科技大学土木工程与力学学院博士后研究人员,中铁第四勘察设计院集团有限公司教授级高级工程师、博士。主要研究方向为大跨结构设计理论与方法。发表论文10余篇。黄 斌,男,1968年生。武汉理工大学土木工程与建筑学院教授、博士研究生导师。高洪波,男,1980年生。中交第二公路勘察设计研究院有限公司工程师。

