基于贝叶斯方法的HPRF雷达跟踪解距离模糊方法
王 娜,王国宏,关成斌,刘兆磊
(1.海军航空工程学院信息融合技术研究所,烟台264001;2.92941部队,辽宁葫芦岛125001;3.南京电子技术研究所,南京210039)
0 Introduction
The range measurement of target is typically ambiguous for radar with high pulse-repetition frequency(HPRF)[1-2].The pulse diversity techniques[3-10]can be used to eliminate range ambiguities,which may be very complex.The multiple HPRF methods are also commonly used to combat range ambiguities[11-19].The traditional multiple HPRF methods require that targets are detected at least on two frames in one dwell,thus can not resolve the range ambiguity when targets are detected on only one frame in each dwell.Although recently existing multiple hypothesis tracking method(MH method)[18-19]proposed by one of the authors can overcome the deficiency of the traditional multiple HPRF methods,it makes a mistake sometimes when the pulse interval number(PIN)changes.
Thus,the PIN and its incremental variable are taken as discrete components of the target state and the problem of range ambiguity resolving and tracking is converted to a hybrid estimation problem in a Bayesian framework,which contains both continuous components such as target states and discrete components such as PIN and its incremental variable.The particle filter is employed to solve the hybrid estimation.
1 Problem formulation
Consider a set of HPRFs used for range ambiguity resolving denoted by Fi,i=1,…,I,and suppose the i th HPRF in this set,Fiis selected.Rmaxis assumed as the maximum range of interest and the corresponding maximum unambiguous range Ruiis given by

where C is the speed of light.
As illustrated in Fig.1,assume the ambiguous range measurement ri(k),ri(k)≤Ruiat time k.All possible ranges rili(k)are generated by
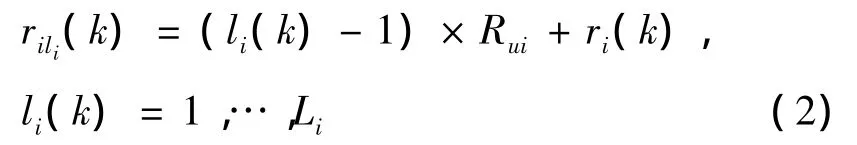
where Li=Ceil(Rmax/Rui)and Ceil(·)means to round the variable toward infinity and li(k)is PIN.
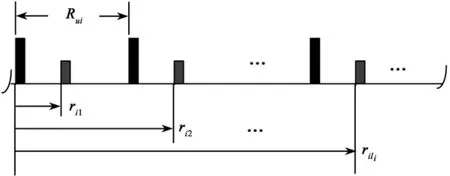
Fig.1 All possible ranges from one range measurement
From Fig.1,any range among rili(k)will appear to be only ri1(k)and there is no direct way of telling which is the true target range.Therefore,it is necessary to provide an integrated approach to the joint estimation of the target state and li(k).Since the target states are continuous,while the value of li(k)is discrete,it is natural to regard the problem of simultaneous range ambiguity resolving and tracking as a hybrid estimation problem.
2 Hybrid state model
The hybrid state model is formulated in polar coordinates.Assume a 2-D radar detector locating at the origin of the coordinate system and employed for detection of a single target with constant velocity.
2.1 Dynamic stochastic process model
The target state contains range and radial velocity as
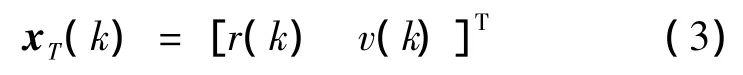
where T denotes the vector or matrix transpose.
The state propagation from k to k+1 is given by

where the transition matrix FT(k)and the distribution matrix of process noise GT(k)are defined respectively
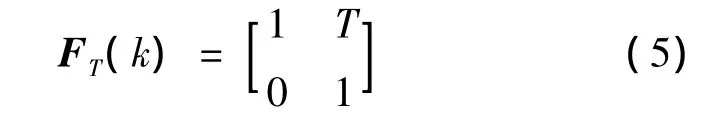
and
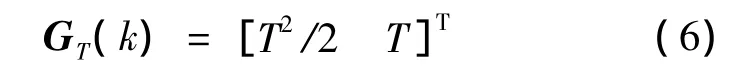
T is the sampling interval,and VT(k)is a zero-mean white process noise characterized as
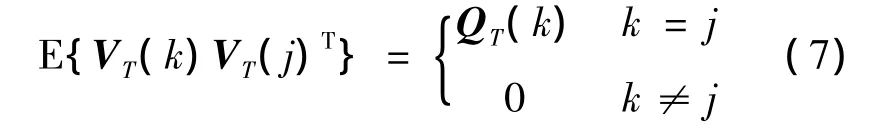
Let
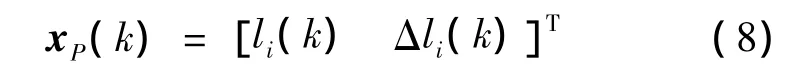
li(k)is PIN of the i th HPRF at time step k andΔli(k)denotes its incremental variable.The dynamic equation can be modeled as
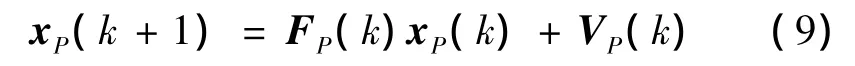
VP(k)is a process noise term with zero-mean and variance QP(k),and the transition matrix FP(k)is
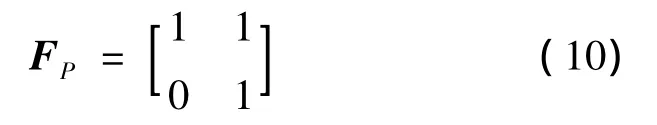
Let
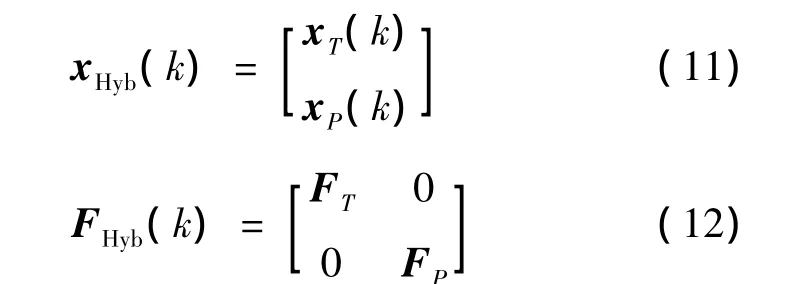
and
The dynamic stochastic process model for this hybrid system can be written as
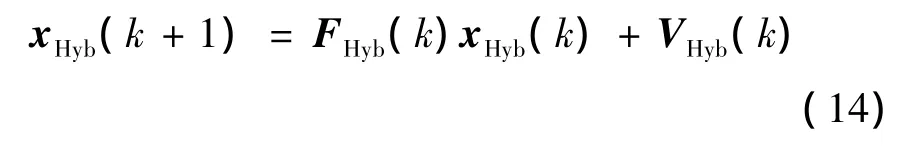
Assume that target can not be out of one maximum unambiguous range in one time interval.Thus the state model of li(k)can be simplified as

It can be seen from(16)thatΔli(k)can be one of the set{-1,0,1}at each time step,but its estimate directly by EKF is continuous.Therefore,thresholds are required to get a discretized estimate.This results in the problem to choose the thresholds.In order to avoid this,the target hybrid state in(11)can be diminished as
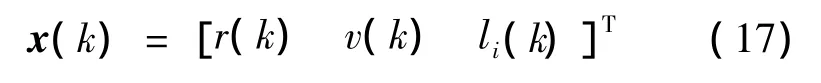
and the dynamic equation(14)is equivalent as
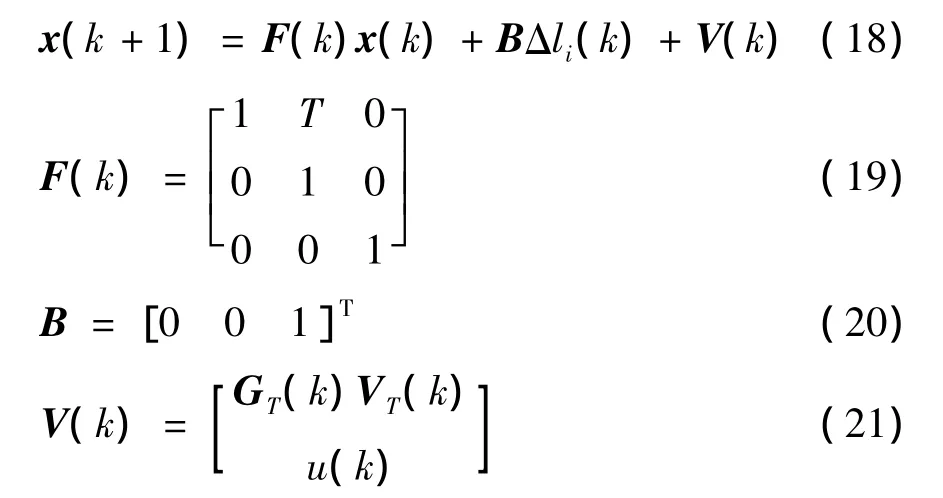
GT(k)and VT(k)defined as(6)and(7)and u(k)is a noise with variance Q(k)deduced as follows.
Since li(k)is a discrete random variable and it takes a random value from the set of{1,2,…,Li}with probability,its expected value and variance can be
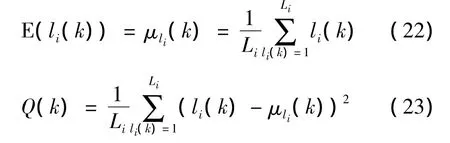
SinceΔli(k)is one value out of{-1,0,1},it can be a three-state Markov chain.Assumeπab,a,b=1,2,3 the mode transition probability forΔli(k)switching from mode a to mode b.The transitional probability matrix is

2.2 Measurement model
The measurement equations at time step k is
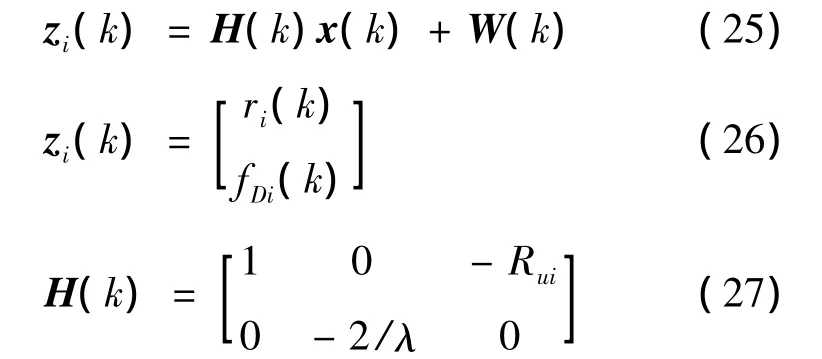
λis wavelength,Ruiis given by(1)and W(k)is zeromean,white Gaussian noise process with known covariance R(k)as
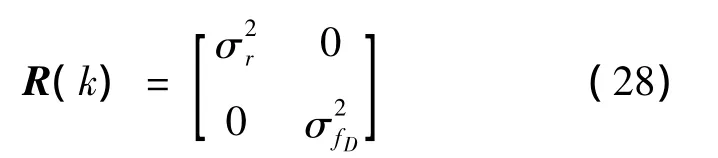
Therefore,the hybrid system can be described by(18),(24)and(25).
3 Conceptual solution in the Bayesian framework
It is well-known that Jump Markov linear systems are convenient models for systems that exhibit both continuous dynamics and discrete mode changes[20-21],then the hybrid system above can be converted as:
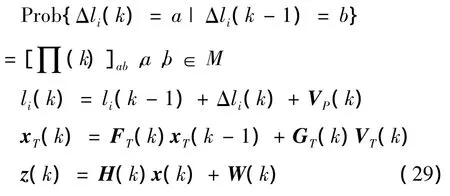
The range ambiguity resolving can now be formulated in the framework of recursive Bayesian estimation.Give the joint posterior probability density function(pdf)of target hybrid state at time step k-1 as
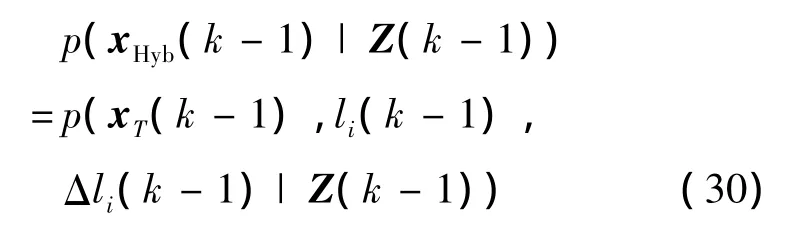
and z(k),the goal for hybrid filtering is to construct the pdf p(xT(k),l(k),Δli(k)|Z(k))at time step k.Define Z(k)={z(1),…,z(k)}.Following theorem and proof are given.
Theorem 1.The recursion for the posterior probability density function is given by
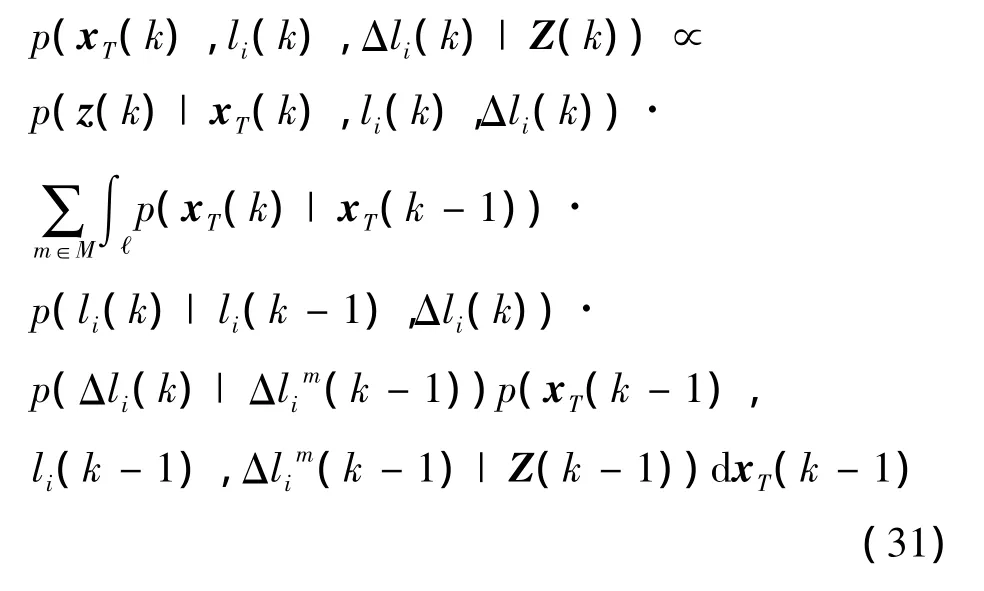
Proof.By application of Bayes rule we obtain
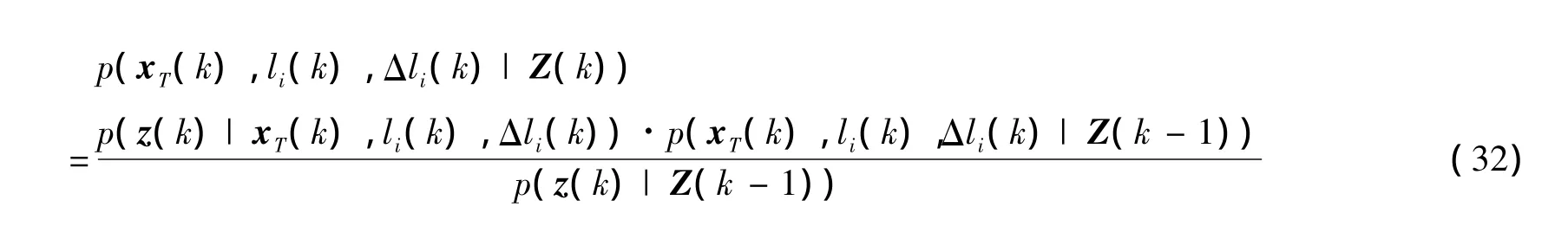
The denominator is neglected in the proceeding,for it is a normalizing constant,independent of the state
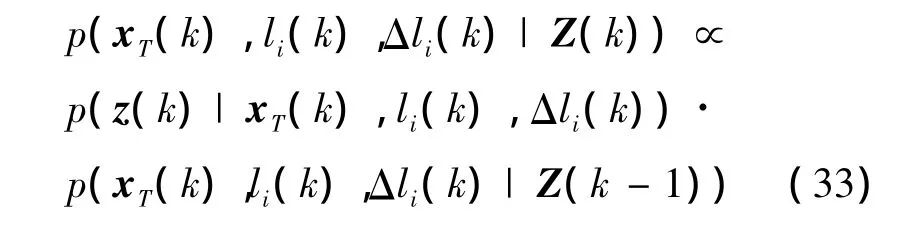
with the identity p(x)=∫p(x|y)p(y)d y we obtain
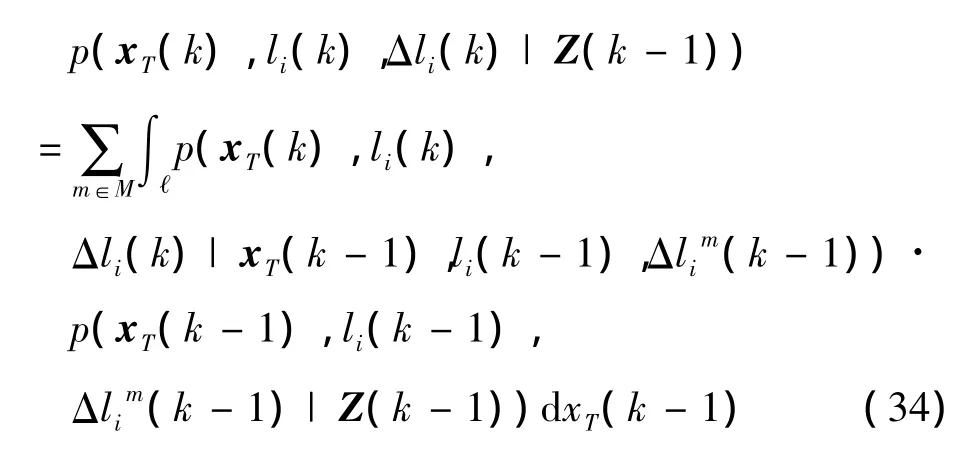
where xT∈ ℓ.
Furthermore,with p(x,y)=p(x|y)p(y)and Δli(k)depending only onΔli(k-1),li(k)depending only on li(k-1)andΔli(k)we can write
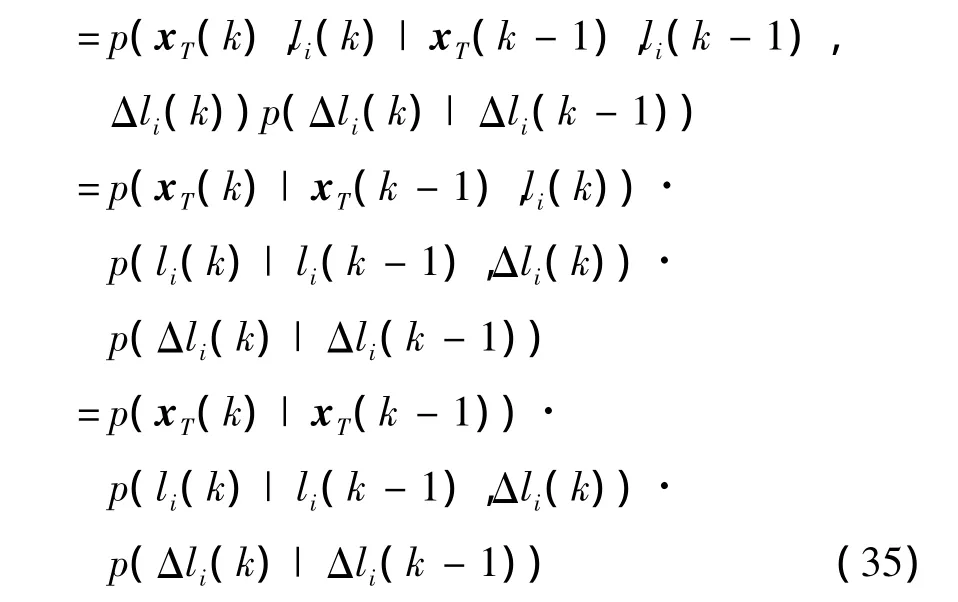
The proof is completed by substituting(34)and(35)into(33).
Conceptually,p(z(k)|xT(k),li(k),Δli(k))can be
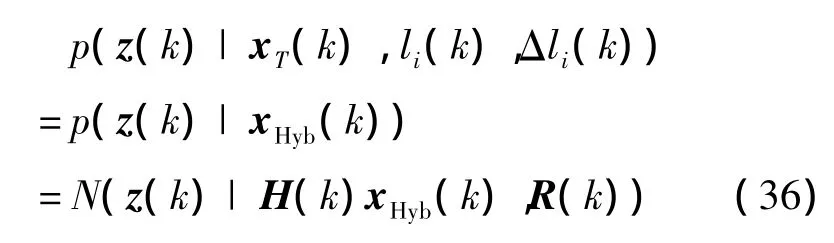
4 A particle filter for simultaneous range ambiguity resolving and tracking
The recursive Bayesian solution of the hybrid systems described in the previous section can be implemented by using a particle filter[21-22].
4.1 A particle filter algorithm process
It is known that the standard algorithm guarantees convergence of the empirical distribution
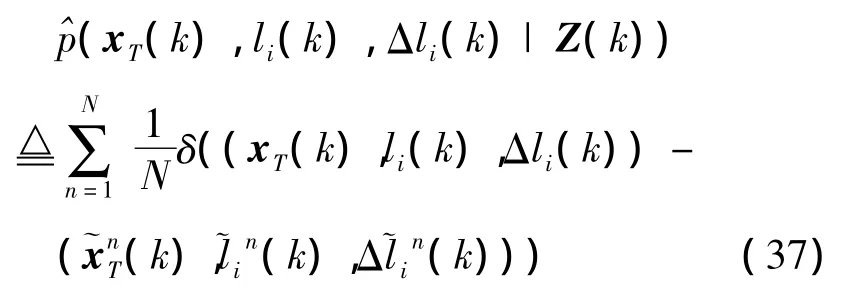
to the true,but unknown posteriori distribution of interest,i.e.p(xT(k),li(k),Δli(k)|Z(k)),if the number of particles N tends to infinity.
As mentioned early,Δli(k)∈{-1,0,1}.Thus particles are implicitly divided into three partitions.The pseudo code of a single cycle of the particle filter algorithm for hybrid estimation is shown in Table 1.
The first step is to generate a random set
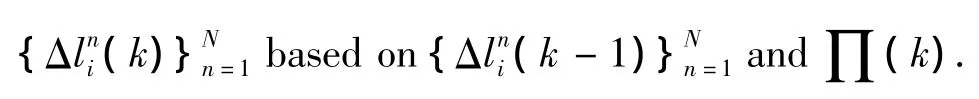
The next step is to predict particle target states according to(18).The remaining steps include normalization of the importance weights and resampling steps[22-23].

Table 1 Particle filter for hybrid estimation
The target state and PIN can be respectively as

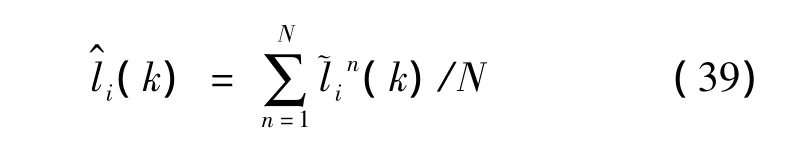
The particle mode state is initialized by samplingaccording to the initial mode probability.The particle target state is initialized based on the initial state of the target in subsection 4.2.
4.2 Initialization of the hybrid state
At time step k,for Fi,rili(k)is obtained by(2),thus all of the possible measurements can be given as
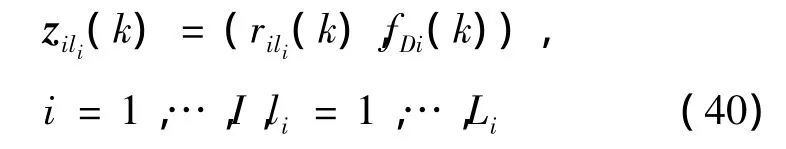
Then,the initial hybrid state estimate of the lith possible measurement for the i th HPRF is
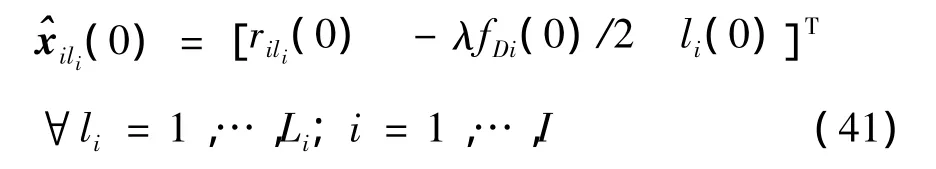
rili(0)and fDi(0)are the measurements in the initial time step.
The range measurements from multiple HPRFs should be the same without considering measurement errors.When considered,the Euclidean distance is used to obtain the initial estimate.Assume(0)and(0)are two possible initial estimated states by the i th and the j th HPRFs.The Euclidean distance between the first two-dimension states ofis
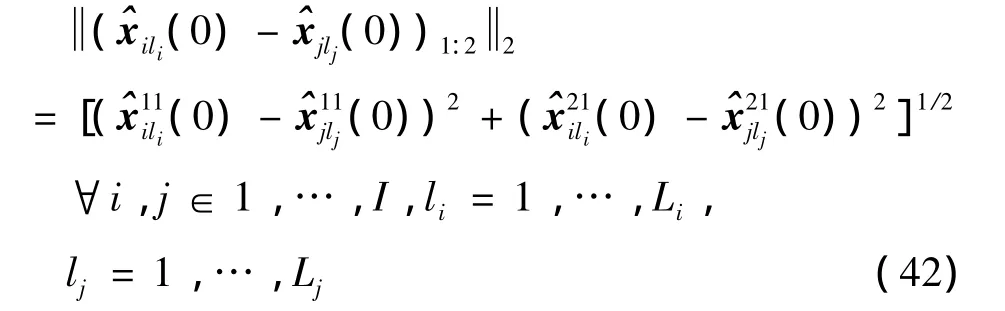
Then,the initial state estimate can be obtained from the minimum distance
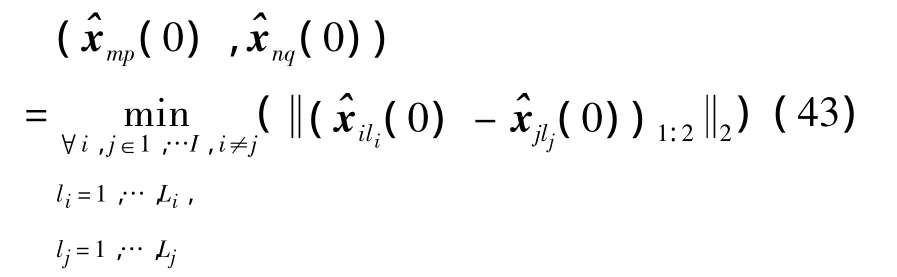
The initial estimates of the m th and n th HPRFs are
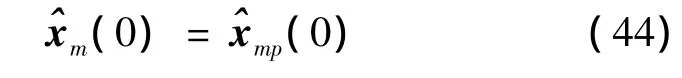
and
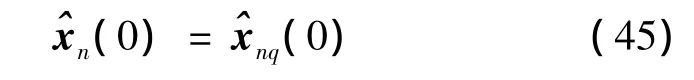
Then the state initialization has been achieved as
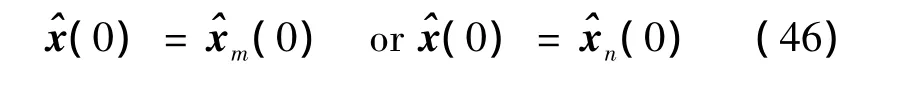
5 Simulation results
The 2-D tracking examples of a single target with constant velocity are presented to demonstrate the proposed method compared with MH method in[18]based on 100 Monte-Carlo runs by two different cases.Take the initial state of the target as(30km,0.2km/s),the process noise as1m/s2,initial mode as1/3,T=1s and k=50.σrandσfDare 100m and 1Hz.Rmaxis 200km.λis 0.1m.Two HPRFs whose repetition pulse interval(PRI)are 37μs and 48μs.Mode transition probability matrix is

5.1 Case 1
It is assumed that the target is detected on PRI1 and PRI2 in the first dwell and by only PRI1 in the remaining time.The simulation results are presented from Fig.2 to Fig.4,where Fig.2 shows PIN estimates from particle filter algorithm,Fig.3 shows the comparison between root mean squared errors(RMSE)of two methods and Fig.4 presents the tracking results.
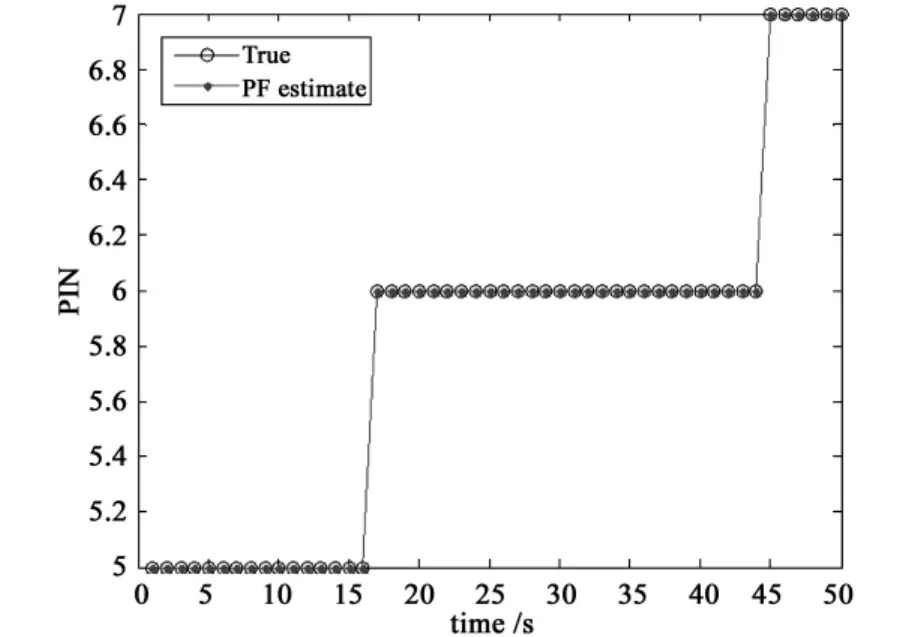
Fig.2 PIN estimate for case 1
It can be seen from Fig.2 that whether PIN changes,PIN estimated by the proposed method are correct.In Fig.3,for the proposed method,range RMSEs are small and convergent.For MH method,range RMSEs are similar with our method in the first 15 time steps and begin to increase and diverge dramatically after the 15th time step.In Fig.4,it can be seen that when PIN changes,tracking results will not be influenced in the particle filter.However,it makes a mistake in MH method.
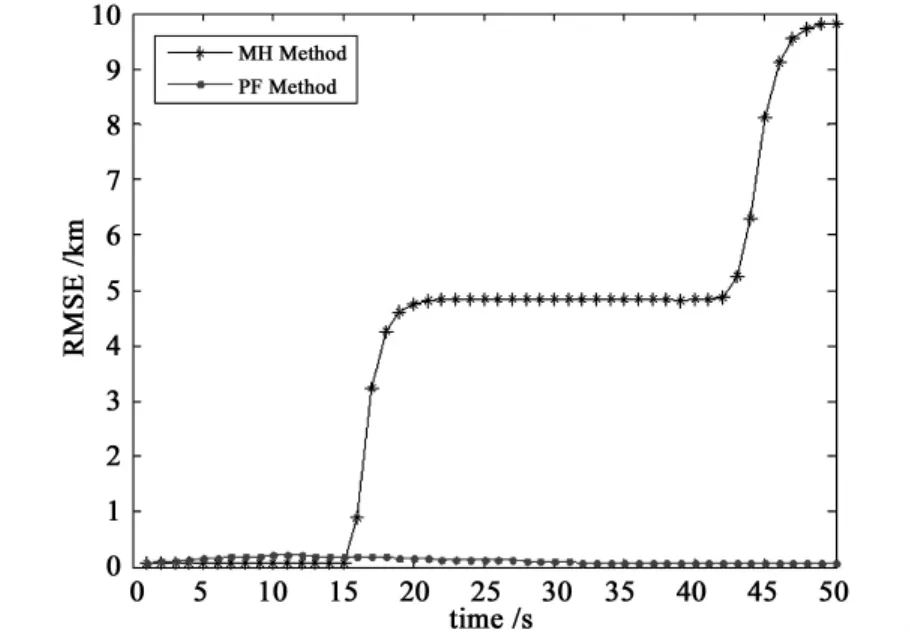
Fig.3 Range RMSE by two methods for case 1
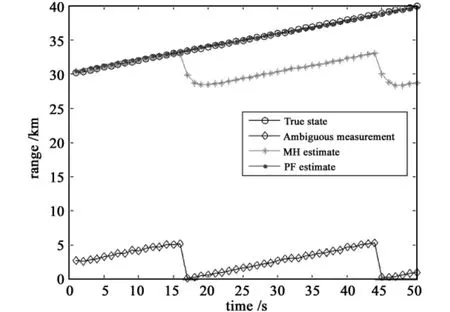
Fig.4 Range estimate by two methods for case 1
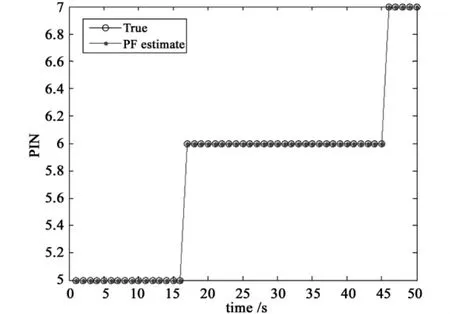
Fig.5 PIN estimate for case 2
5.2 Case 2
It is assumed the target is detected on PRI1 and PRI2 in the first dwell and alternately in the remaining time.The simulation results are given from Fig.5 to Fig.7,where Fig.5 shows PIN estimate from particle filter algorithm,Fig.6 shows the RMSEs comparison between the two methods and Fig.7 presents the tracking results.
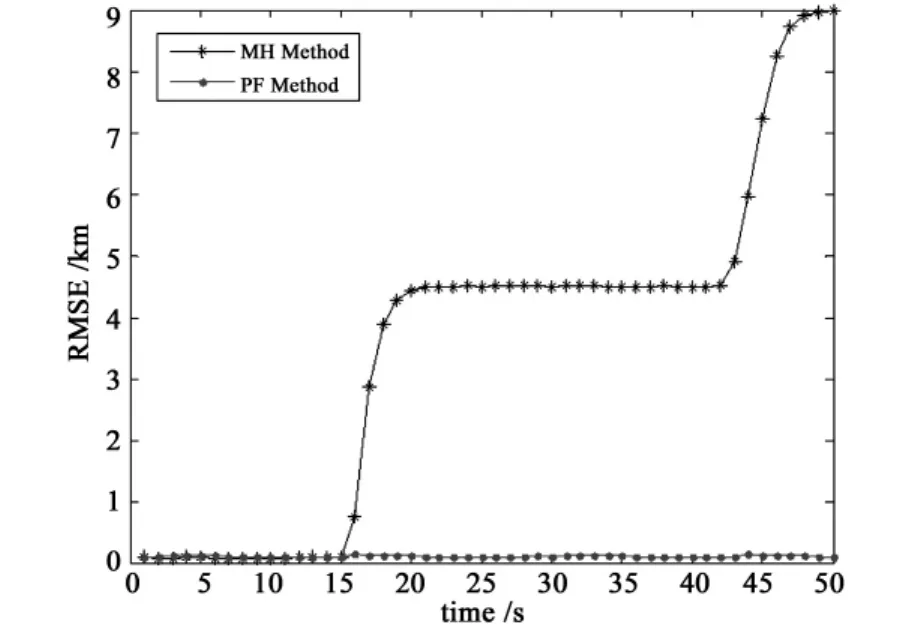
Fig.6 Range RMSE by two methods for case 2
It can be seen from Fig.5 that whether PIN changes,PIN estimated by the particle filter are correct.In Fig.6,for MH method,range RMSEs in the first 15 time steps are similar with our method,and when PIN changes,RMSEs increase and diverge dramatically after the 15th time step;for the proposed method,RMSEs keep small and convergent and will not be influenced by PIN change.It can be seen in Fig.7 that when target detected on different HPRFs alternately,tracking results can still not be influenced with PIN variation in the particle filter.However,it makes a mistake in MH method.
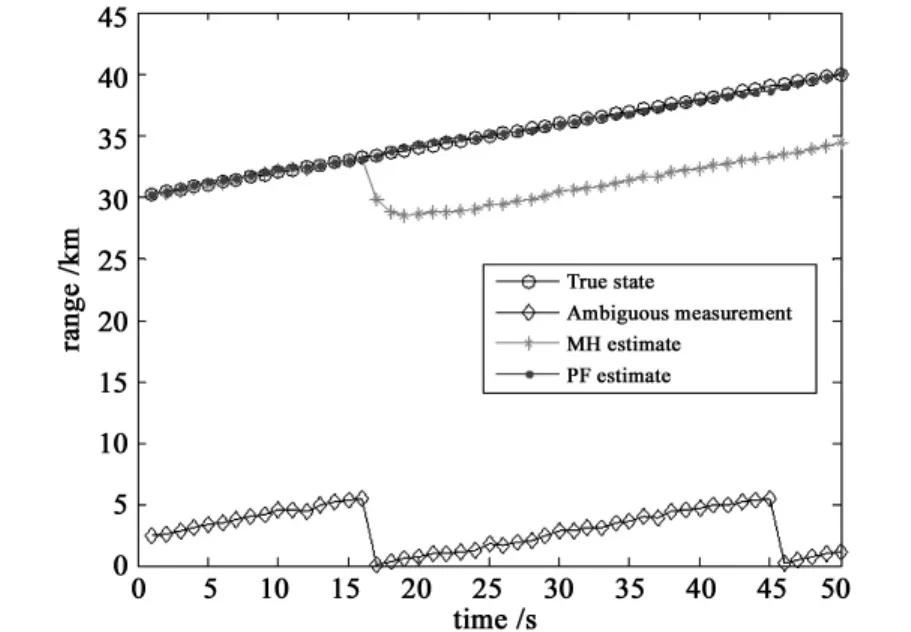
Fig.7 Range estimate by two methods for case 2
6 Conclusions
It is important that the PIN and its incremental variable are considered as target states as proposed.The simultaneous range ambiguity resolving and tracking problem is studied in a Bayesian framework and it is managed by a particle filter.The simulation results demonstrate that the proposed method is not influenced by PIN change and the range estimate can be obtained with high precision.
[1]Stimson GW.Introduction to airborne radar[M].2nd ed.USA:SciTech Publishing,Inc.1998.
[2]Skolnik M I.Radar handbook[M].2nd ed.USA:McGraw-Hill Companies,Inc,1990.
[3]Li L,Ren L X,He PK,et al.Study on range window in HPRF stepped frequency radar system[C].Signal Processing,2008.ICSP 2008.9th International Conference on,Beijing,China,October 26-29,2008.
[4]Ren L X,Mao E K.Study on HPRF pulsed Doppler stepped frequency radar system[C].Radar,2006.CIE’06.International Conference on,Shanghai,China,October 16-19,2006.
[5]Strecker A,Wieszt A,Al-Youssof N,et al.Method for detecting targets and determining their distance via an HPRF radar system.Compiler:US,7151481B1[P/OL].2005-11-09[2006-12-19].http://www.freepatentsonline.com/7151481.html
[6]Duan J Q,He Z S,Qin L.A new approach for simultaneous range measurement and Doppler estimation[J].IEEE Geoscience and Remote Sensing Letters,2008,5(3):492-496.
[7]Deng H,Himed B,Wicks M C.Concurrent extraction of target range and Doppler information by using orthogonal coding waveforms[J].IEEE Transactions on Signal Processing,2007,55(7):3294-3301.
[8]Levanon N.Mitigating range ambiguity in high PRF radar using inter-pulse binary coding[J].IEEE Transactions on Aerospace and Electronic Systems,2009,45(2):687-697.
[9]Akhtar J.Cancellation of range ambiguities with block coding techniques[C].Radar Conference,2009 IEEE,Pasadena,CA,May 4-8,2009.
[10]Tao H H,Liao G S.Bi-phase encoded waveform design to deal with the range ambiguities for sparse space-based radar systems[J].Journal of Astronautics,2005,26(5):657-662.
[11]Thomas A G,Berg MC.Medium PRFset selection:an approach through combinatorics[J].IEE Proceedings-Radar,Sonar and Navigation,1994,141(6):307-311.
[12]Zhou R,Gao M G,Dai Q Y,et al.Analysis and simulation for ambiguity resolving using residues’difference look-up table[J].Systems Engineering and Electronics,2002,24(5):30-31,102.
[13]Lei W,Long T,Zeng T,et al.The resolution of range ambiguity in a medium pulse Doppler radar[J].Journal of Beijing Institute of Technology,1999,19(3):357-360.
[14]Zhang L,Mu H Q.MPRF instrumentation radar PRF design[J].Systems Engineering and Electronics,2008,30(6):1191-1194.
[15]Jiang K,Li M.A novel algorithm for PD radar range resolving ambiguity[J].Fire Control Radar Technology,2008,37(2):25-28.
[16]Wang JM,Yang J,Wu SJ.A new algorithm of range ambiguity resolution for Pulse Doppler radar[J].Radar and ECM,2005,(3):38-41.
[17]Zhou H P,Sha X S,Zhang G F.Resolving range ambiguity of weather radar using batch processing method[J].Modern Radar,2006,28(11):20-21,32.
[18]Liu Z L,Guo Y C,Zhang G Y,et al.Multiple models track algorithm for radar with high pulse-repetition frequency in frequency-modulated ranging mode[J].IET Radar Sonar Navigation,2007,1(1):1-7.
[19]Liu Z L,Zhang G Y,Xu Z L,et al.Multiple hypothesis track algorithm for airborne fire control radar with HPRF in FMR mode[J].ACTA ARMAMENTARII,2007,28(4):431-435.
[20]Blackmore L,Rajamanoharan S,Williams B C.Active estimation for jump Markov linear systems[J].IEEE Transactions on Automatic Control,2008,53(10):2223-2236.
[21]Boers Y,Driessen H.Hybrid state estimation:a target tracking application[J].Automatica,2002,38(12):2153-2158.
[22]Ristic B,Arulampalam S,Gordon N.Beyond the kalman filterparticle filter for tracking application[M].USA:Artech House,2004.
[23]Cheng SY,Zhang JY.Review on particle filters[J].Journal of Astronautics,2008,29(4):1109-1111.
- 宇航学报的其它文章
- 基于分段连续推力的晕轨道控制方法

