基于分段连续推力的晕轨道控制方法

晁 宁，李言俊

(西北工业大学航天学院，西安710072)

0 引言

众所周知，平动点附近的晕轨道具有指数不稳定性，因此对运行在其上的探测器进行轨道保持是十分必要的。而自从开始了各种平动点空间任务，晕轨道保持控制就一直是研究的热点。Farquhar［1］和Breakwell［2］最早提出了target控制模式。随后Giamberardino基于线性模型设计了渐近稳定的非线性控制器，实现了Halo轨道的渐近跟踪和扰动补偿［3］。Howell等［4］同样基于线性化模型的思想，给出了控制器精度与能耗均满足要求的折中策略。David Cielaszyk和BongWie［5］提出了用LQR线性二次型最优控制方法来保持晕轨道的稳定。Rahmani［6］利用最优控制理论中极值曲线的变分成功求解了两点边值问题，实现了Halo轨道维持。考虑到最优控制求解的难度，Ming Xin等［7］提出了用于近似求解HJB方程的θ－D方法，这种方法具有很高的实时性。胡少春等［8］将序优化理论与微分修正法相结合，优化了晕轨道的入轨机动问题。这种方法在优化过程中具有收敛速度快、对初值不敏感与计算量小的优点。

基于最优控制思路的方法在Halo轨道维持中具有较高控制精度，但在每个控制点求解系统微分方程组时需要进行大量计算且具有较多控制点，系统实时性能受到影响。而θ－D法虽具有很高实时性但属于次最优方法。本文在三体模型误差线性模型的基础上，利用有限时间调节器问题推导了晕轨道周期内的连续小推力控制方案。针对整周期控制方式在超调后状态量收敛速度慢的问题，通过分段连续推力模式来近似瞬时脉冲推力控制模式，给出了最短分段控制时间的计算方法。方法基于小偏差假设对非线性模型进行了线性近似，以最优控制方案推导线性反馈控制律。同时在整个Halo轨道周期仅需1～2个控制点，减小了计算量且使得系统结构简化。仿真实验表明，控制方法能够根据实际轨道与标称轨道偏差的大小，调整控制时间区间长度，以尽可能低的能耗快速消除探测器入轨状态偏差。

1 无摄三体模型

天体力学中多数情况都可描述为一个质量忽略不计的小天体P在两个相互环绕运动的大天体P1、P2(P1＞P2)引力作用下的运动状态，这是比二体模型更精确的一种合理近似。对于圆限制性三体问题，通常利用以两大天体质心为圆心旋转的会合坐标系或称旋转坐标系来研究。假定P不影响P1、P2的运动，两大天体共同绕其质心做角速度为ω的圆周运动。P1指向P2的方向为会合坐标系的x轴，ω方向为z轴，y轴与x、z轴成右手系。这种假设下的动力学模型不考虑摄动因素，即无摄圆限制性三体模型，小天体的无量纲化运动对应一个二阶常微初值问题

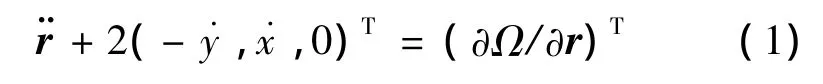
分量形式为

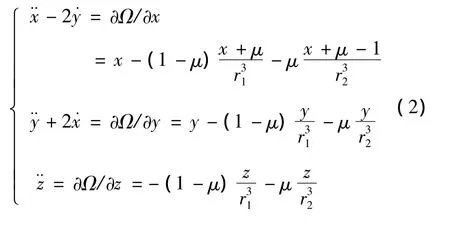
其中，Ω(x，y，z)=(x2+y2)/2+U(r1，r2)，引力势函数U(r1，r2)=(1－ μ)/r1+μ/r2，μ=m2/(m1+m2)是航天器到大天体的距离是航天器到小天体的距离。

对于该CRTBP目前仅找到5个特解和一个Jaccobi积分［9］。前者对应5个引力平衡点，其中三个共线平衡点不稳定，位于两大天体连线上，记作Li(i=1，2，3);两个三角平衡点Lyapunov稳定。由于前两个点的应用价值较大，引发了学者们的深入研究。五个平衡点处对应的Jacobi积分常数Ci(μ)有如下关系:

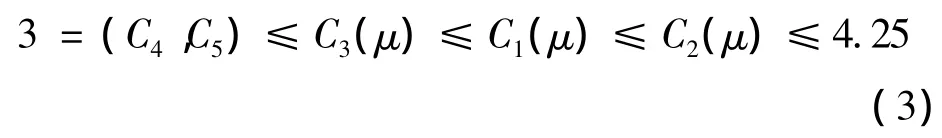
曲面2Ω(x，y，z)=C即为零速度面。

2 无量纲化

对于三体模型来说，地月系统数据量级一般都比较大。为了简化计算，需要利用无量纲化方法对计量单位进行省略并将数据缩小相应倍数。地月系数据计算中无量纲化时对应的长度时间和质量单位分别为:

［M］=m1+m2——两天体质量

［L］=3．84401×105km，［M］=6．0477×1024kg，［T］=3．7519×105s

因此，月球的无量纲质量为μ=0．012153，地球的无量纲质量为1－μ。若按照1年为365．25个平太阳日计算，则1年和1天分别是3．15576×107s和8．64×104s，无量纲化后的时间为84．1110和0．2303。无量纲速度V00和实际速度(km/s)的转化关系为

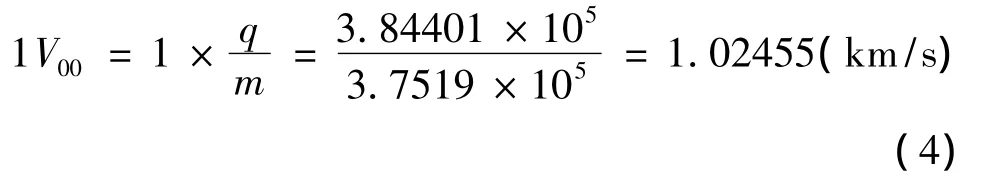
式(4)表示了地月系中一个单位的无量纲速度与实际速度的关系。其中q、m分别表示无量纲系统中的距离和时间。同样可以得到无量纲加速度a00和实际加速度的转换关系为

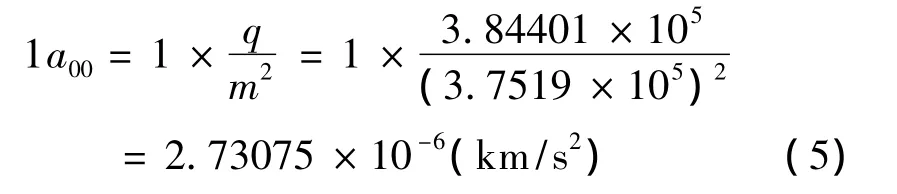
3 特性分析及线性化

3．1晕轨道特性

3．1．1不稳定性

晕轨道是存在于共线平动点附近的一类周期轨道。这种轨道具有指数不稳定性，发散快，并且对初始值十分敏感。即使不考虑摄动因素，并且入轨精度均达到10－8(10m)的量级，无控的晕轨道最多也只能维持3个周期左右(以THalo=13．5808天为例)，之后就开始发散，如图1所示。利用Richardson三阶近似解获得的轨道虽然能够较准确地表现轨道的三维周期运动，但它是理想化的解模型，不能够体现出晕轨道的弱稳定性。考虑到入轨误差和各种实际因素引发的模型变异，需要对在轨探测器按照偏离规律进行轨控。

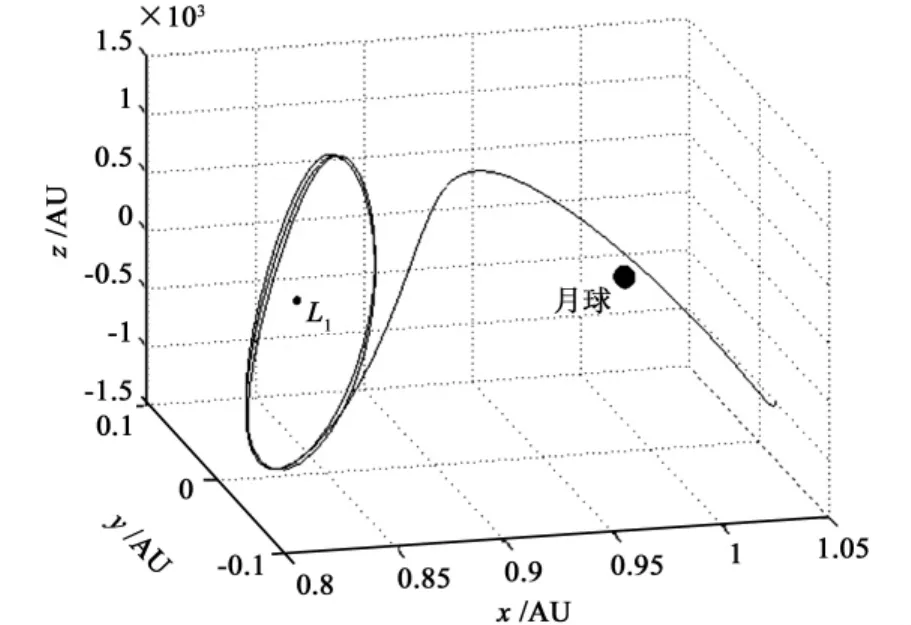
图1 地月系L1点某晕轨道Fig．1 Earth-Moon system L1 point some halo orbit

3．1．2周期性

原系统线性化模型中的系数矩阵A是时变的。但是在理想入轨状况下，经历了n个晕轨道周期的时间后，A中的元素具有不变性，即

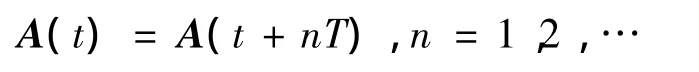
于是，线性化后的时变系统就可以化为单个周期内的定常系统。系统矩阵元素依积分起始点而定。因此晕轨道上所有点的状态都能够作为积分起始点，只要积分周期为轨道周期的整数倍，时变系统就能够化为定常系统，从而简化计算。

3．1．3可控性

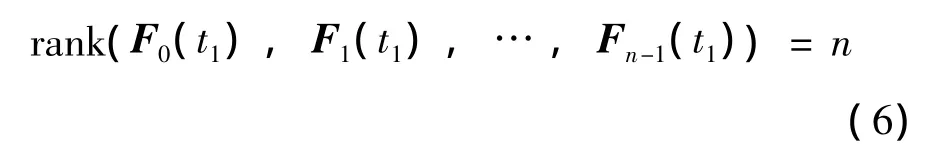
其中

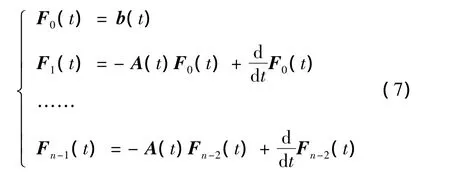
取定系统矩阵A(t)为多元向量函数f(X)的雅克比矩阵，控制矩阵b为增广单位阵［03I3］T。从式(9)可以看出，系统仅需要对后3阶进行控制，因此分析可控性前首先将系统降为3阶。控制矩阵b取为I3，则从上式中容易看到可控性矩阵满秩，线性时变系统可控。

系统矩阵A(t)是以状态向量X(t)为变量的函数。以晕轨道上任意点为研究对象时，时变系统又能够转换为定常系统。线性定常系统完全能控的充要条件为

其中n为系统阶数。线性系统可控性特征为:

(1)系统在平动点处可控;

(2)一个周期内，晕轨道上所有点对应的可控性矩阵序列K(t)均满秩，t∈［t0，t0+THalo］。

将线性时变系统式在各轨道机动点处做定常变换后，容易验证对应的(8)式是成立的。因此误差线性系统在小偏差范围内是完全可控的，其上所有点都能够作为系统控制作用u的施加点。

3．2线性化

用于深空探测的无摄圆限制性三体模型表现出很强的非线性，在考虑摄动因素后这种非线性特性就更加明显。而当前比较成熟的控制律多数以线性系统为研究对象，并且具有良好的控制效果与鲁棒性。当实际轨道与标准轨道的状态误差不大时，误差线性系统模型具有较高的准确度。通常用到的线性化方法有两种:

(1)将误差状态作为新的状态变量，利用多元向量函数的雅克比矩阵作为线性系统的系数矩阵;

(2)仍以原位置速度作为状态量，将动力学系统转换关系作为系数矩阵。

本文以前者作为研究重点进行分析，不对后者详细叙述。

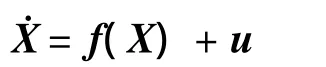
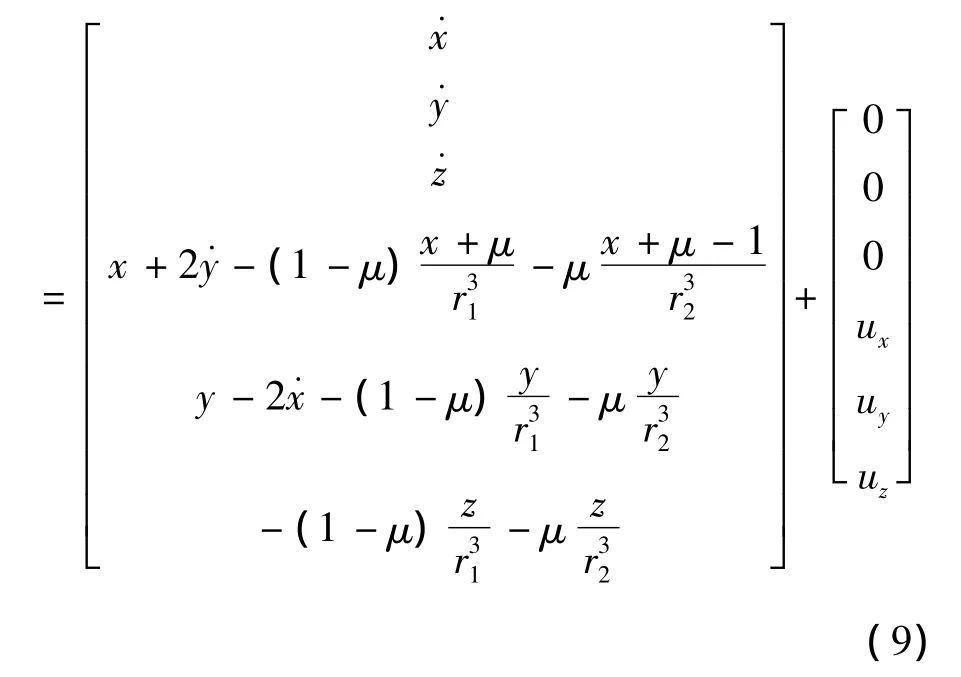
对上式微分并在平衡位置进行一阶泰勒展开，可得

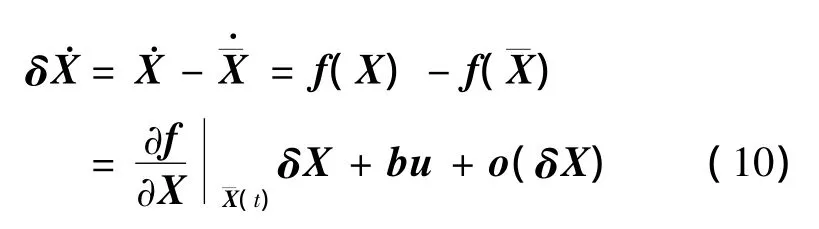
忽略高阶项，并取向量函数的雅克比矩阵为系数矩阵，即

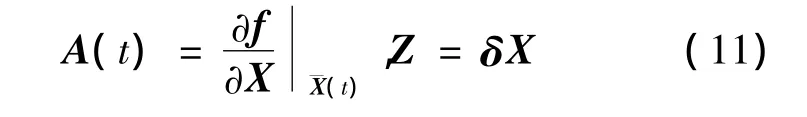
雅克比矩阵为

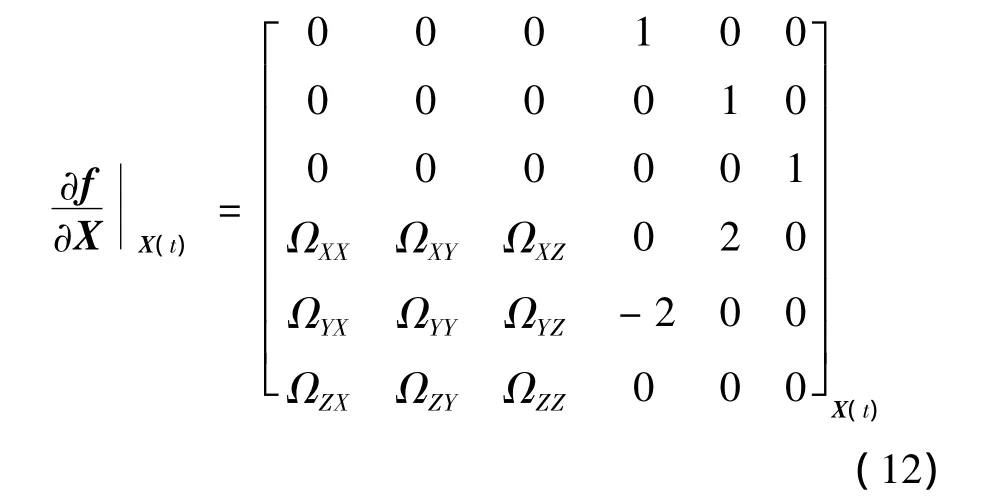
计算可知，处于晕轨道状态时，交叉项均为0。于是，非线性系统可近似化为线性系统

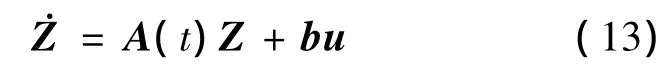
这种方法在小扰动情况下具有较高准确性。在此假设下，可以通过选择能量函数通过使其非正定获得控制律，或者选择线性调节器的指标函数利用极小值原理或动态规划法求解到控制律u(t)。同时可以近似认为扰动周期与轨道周期相同，即TR=T。

上面A(t)为系统矩阵，其中变量元素的值会随探测器在会合坐标系中的位置而变化。对误差线性系统来说，控制器设计的目标即推导出合适的控制向量u，使得误差系统状态量~X＜ε，ε为正常数。

4 最优控制方法

轨道保持过程中要求以最小的速度增量实现最高的位置精度，这样的控制要求类似于最优控制中对性能指标的表述。因此考虑利用极小值原理及Riccati方程来推导一个THalo内的小推力连续控制方案。

4．1整体连续推力控制(Total Continuous Thrust Control，TCTC)

以一个晕轨道周期T为控制区间，取有限时间线性调节器性能指标为

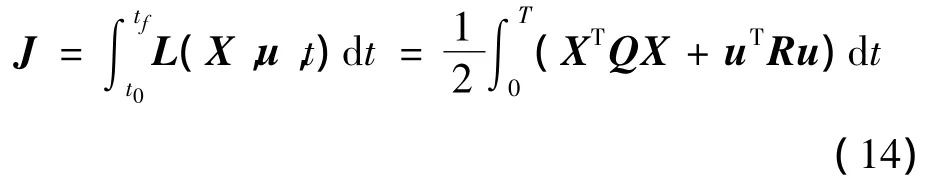
终端固定，其状态约束为X(tf)=0。因此，单周期晕轨道控制问题属于终端固定的有限时间状态调节器。式(14)中Q＞0、R＞0分别为加权矩阵，用来控制各分量的比重。通常Q为对角阵，各个元素取状态向量对应量纲数量平方的倒数。

Hamilton函数取为

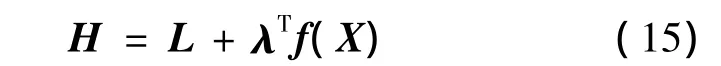
根据线性调节器问题相关结论［11］，要求K(t)阵满足对称正定和逆Riccati方程，即

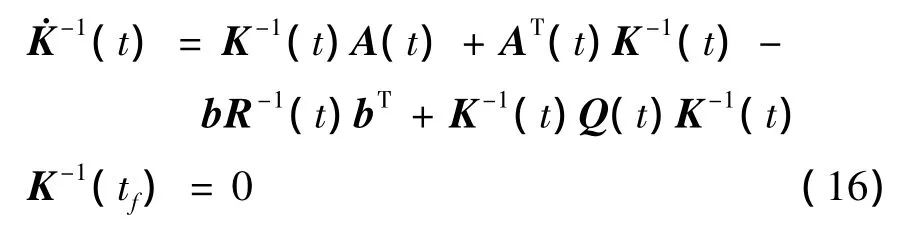
线性动力学误差系统对应Riccati方程阶数较高，通常利用数值积分进行求解来提高运算速度。积分中需要注意到:如果按照时间反向推演的方向进行积分，数值积分的初值就是Riccati方程解的终值，即K－1(tf)=0。因此设置K(0)=［0，…，0］，K∈Rk(n)，其中为系统矩阵阶数。因此可以在以每个晕轨道周期为单位求解Riccati方程来构造反馈控制律。

于是有最优控制

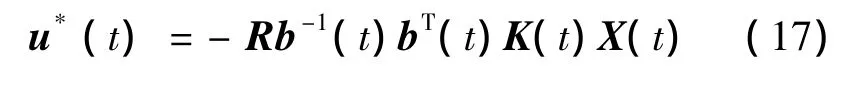
设总的控制量为

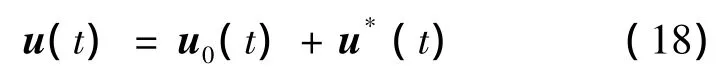
式中u0(t)为变轨需要的加速度。当飞行器通过一次推力由L1点稳定流形进入晕轨道运行时，u0(t)=0，于是控制总量u(t)=u*(t)。

最优轨迹为下面一阶线性微分方程的解

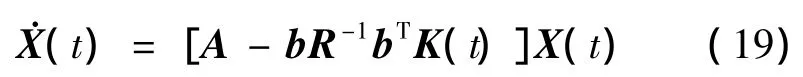
4．2分段连续推力控制(Segmental Continuous Thrust Control，SCTC)

小推力控制模式具备一定的优势，如推力稳定，线性特性好。但是这种方式控制周期长，施控前后时间系统较难统一，在某些需要付出较高能耗来实现轨道快速跟踪的场合就不合适使用。SCTC模式的主要方法就是缩短控制区间，以此来近似瞬时脉冲推力模式，使其兼具连续推力控制与脉冲控制的优点。轨道修正时，每一个分段连续控制区间被模拟为瞬时推力模式的一个脉冲。通常每条晕轨道都会事先规划2～3个机动点，这些机动点处就是每个分段控制器开始工作的位置;而控制器的工作时间就由控制区间tf－t0确定。

但是SCTC模式存在一个限制:如果入轨误差比较大，并且要求航天器在较短的时间内收敛至标准轨道，就需要提高机动加速度，而这样又会造成振荡加剧，这样也会影响航天器的控制性能。因此，不同的状态误差就对应了不同的连续推力模式能够接受的最短控制时间min(Tcon)。

为使得控制向量在规定的时间内到达零点附近，结合小推力模式提供的机动能力，能够获得一个基本保持不变的阈值。具体来讲，利用距离误差除以控制时间，能够获得一个速度阈值;而利用速度误差除以控制时间，能够获得一个加速度阈值。结合小推力模式下飞行器能够提供的变轨能力和实验数据，在地月三体系统中，飞行器进行轨道修正能够承受速度和加速度选择如下经验值:

无量纲速度:V00=7．4006×10－4;

无量纲加速度:a00=0．001365。

当给定了入轨的初始状态误差，通过上面两个阈值能够确定两个控制时间，即

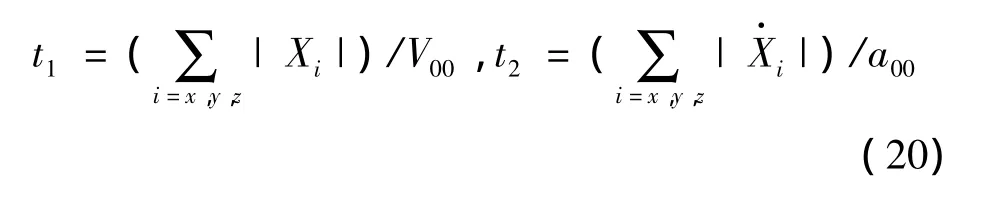
为了保证修正轨道的收敛性，当t1≠t2时，控制区间Tcon=max(t1，t2)。

5 仿真分析

5．1不同等级入轨误差的控制效果比较

由于地月系单位长度为地月均距约为3．8×105千米，因此初始状态包含了方差为10－6的随机高斯噪声扰动，意味着存在100m级的偏差。

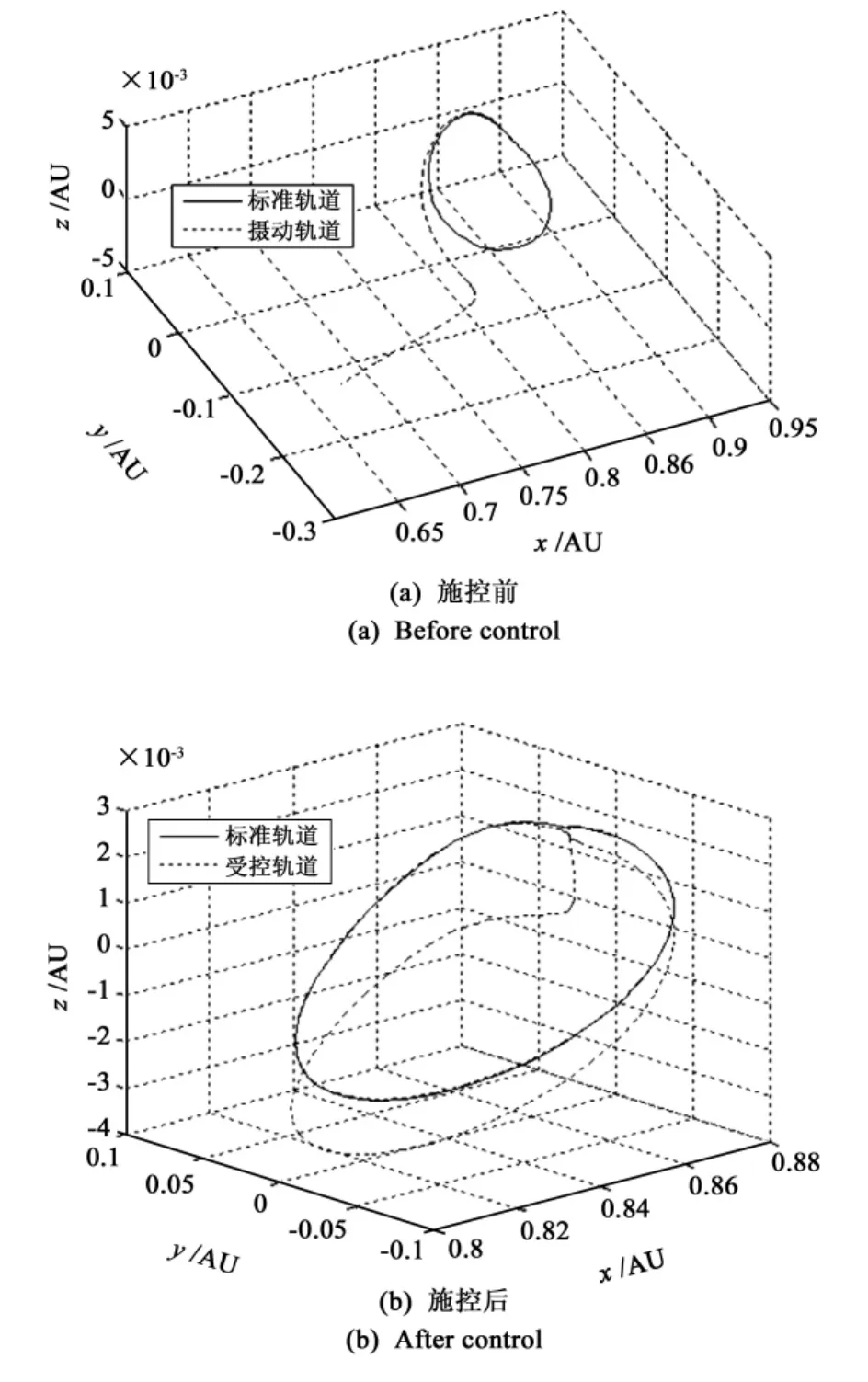
图2 误差等级σ2=10－6时轨控前后情况Fig．2 Orbit control situation under the error grade ofσ2=10－6

可以看出，通过线性最优控制，状态曲线在经过若干个减幅振荡周期后，能够在有限时间内(THalo=12．33天)逐渐收敛至标准晕轨道。同时，入轨误差等级大，轨道发散严重，受控轨道振幅也就大。另外，小推力控制的优点是能量消耗低，所有能耗被分配整个轨道，使得每时刻的能量需求很小。以图2的情况为例，整个晕轨道周期中三轴消耗的总速度增量共4．7782×10－6m/s。

5．2 SCTC模式与TCTC模式对比

以10－6入轨误差等级的某个初值为例，比较了SCTC和TCTC模式下的控制效果，如图3。从图3中比较可以看出，分段连续轨控下实际轨道与标准轨道的贴近度比较高，并且通过1个平太阳日(一个平太阳日的无量纲数为0．2303)左右的时间实际轨道基本收敛至标准轨道。一个晕轨道周期实施1～2次状态反馈控制即可。

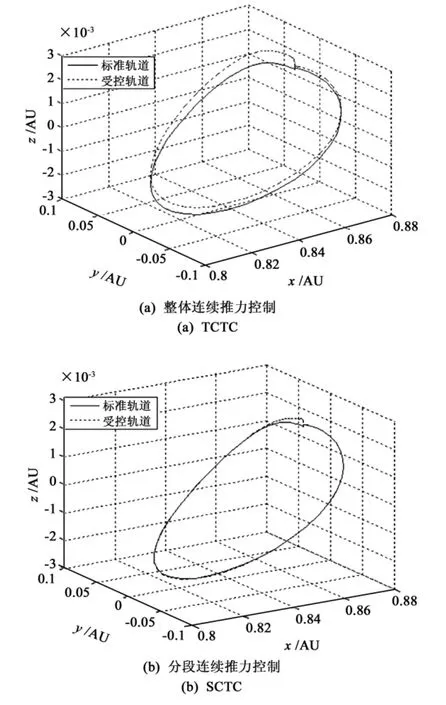
图3 两种轨控效果对比Fig．3 Contrast of two kinds of orbit control effect

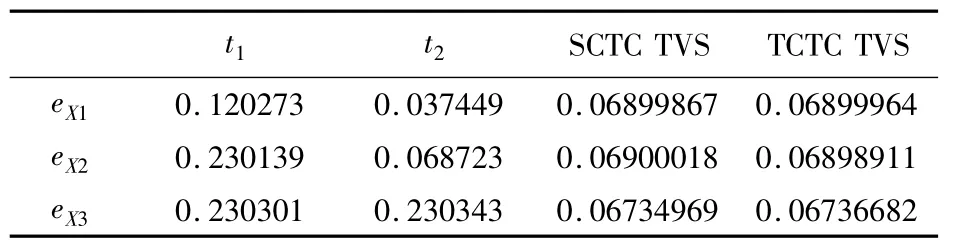
表1 不同eX对应的最佳控制时间及跟踪方差和(一个平太阳日的无量纲数为0．2303)Table 1 Best control time and sum of tracking variance corresponding to different eX

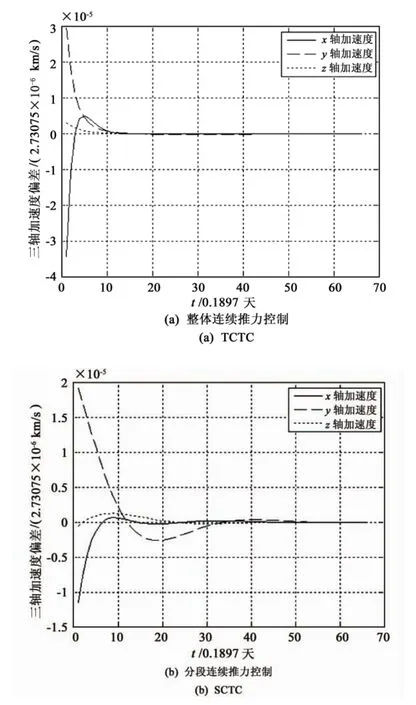
图4 一个T Halo内的加速度曲线Fig．4 Acceleration curves in a T Halo

下面以10－7、10－6和10－5三个不同入轨误差等级为例，对比分段连续推力模式的控制情况。表1是不同误差eX对应的t1、t2及跟踪结果，跟踪方差和(TVS)表示三轴分量方差在单个THalo内的总和。TVS按照式(21)计算

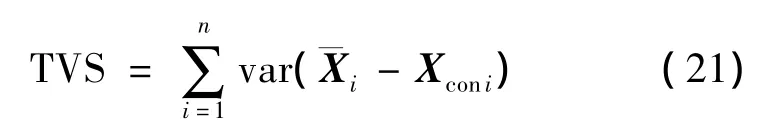
6 结论

本文在小偏差假设基础上将原限制性三体模型问题转换为误差线性模型进行控制方法研究，并利用最优控制方法推导了晕轨道周期内的连续小推力控制方案。结合减少能耗和提高状态量收敛速度的综合考虑，提出分段连续推力控制模式来改善超调后的不良品质，其线性反馈控制律也使得系统结构得到简化。方法能够根据实际轨道与标称轨道偏差的大小，调整控制时间区间长度，以尽可能低的能耗快速消除探测器入轨状态偏差。仿真结果验证了方法的有效性。

［1］Farquhar R W．The control and use of libration point satellite［R］．NASA TR R－346．

［2］Breakwell J V，Kamel A A，Ratner M J．Stationkeeping of a translunar communication station［J］．Celestial Mechanics，1974，10(3):357－373．

［3］Giamberardino P，Monaco S．On halo orbits spacecraft stabilization［J］．Acta Astronautica，1996，38(12):903－925．

［4］Howell K C，Pernicka J．Stationkeeping method for libration point trajectories［J］．Journal of Guidance，Control and Dynamics，1993，16(1):151－159．

［5］Cielaszyk D，Wie B．New approach to halo orbit determination and control［J］．Journal of Guidance，Control and Dynamics，1996，19(2):266－273．

［6］Rahmani A，JalaliM A，Pourtakdoust S H．Optimal approach to halo orbit control［C］．AIAA Guidance，Navigation，and Control Conference and Exhibit，Austin，2003．

［7］Xin M，Dancer M W．Station-keeping of an L2Libration point satellite withθ－D technique［C］．The 2004 American Control Conference，Boston，2004:1037－1042．

［8］ 胡少春，孙承启，刘一武．基于序优化理论的晕轨道转移轨道设计［J］．宇航学报，2010，31(3):662－668．［Hu Shaochun，Sun Cheng-qi，Liu Yi-wu．Transfer trajectory design for halo orbit based on ordinal optimization theroy［J］．Journal of Astronautics，2010，31(3):662－668．］

［9］ 俞辉，宝音贺西，李俊峰．双三体系统不变流形拼接成的低成本探月轨道［J］．宇航学报，2007，28(3):637－642．［Yu Hui，BaoYin He-xi，Li Jun-feng．Low energy transfer to the Moon using the patching of invariant manifolds of two there-body systems［J］．Journal of Astronautics，2007，28(3):637－642．］

［10］ 阙志宏，周凤岐，罗健，等．线性系统理论［M］．西安:西北工业大学出版社，1994．

［11］ 程国采．弹道导弹制导方法与最优控制［M］．长沙:国防科技大学出版社，1987．