基于无奇异变换的卫星广播星历拟合算法

文援兰，刘光明，张 志

(国防科技大学航天与材料工程学院，长沙410073)

0 引言

导航卫星星历可以分为精密星历和广播星历两类，前者精度高，用于事后轨道修正，后者由地面主控站计算得到，通过卫星发布给用户，精度相对较低，但是可用于实时导航定位。利用地面精密测轨数据拟合导航卫星广播星历参数，是用户使用全球卫星定位系统进行动态导航定位的关键［1］，而导航卫星广播星历拟合误差都会直接影响用户的导航定位精度。文献［2］对GPS广播星历参数的拟合算法及其精度评估进行了研究，文献［3］研究了GPS广播星历参数中的调和项系数对广播星历参数的拟合算法的影响。文献［4］针对静止轨道卫星轨道倾角近似为0，致使卫星轨道的升交点定义模糊，研究轨道倾角变换拟合广播星历参数的方法。文献［5］针对星载计算机的处理能力有限，引入基于遗忘因子的递推最小二乘估计算法，研究了在轨实时拟合广播星历的方法。目前，许多国家都在加紧建设自己的卫星导航定位系统，其导航卫星广播星历参数拟合算法及星历误差分析是重点研究方向［6－7］。

针对由于卫星轨道的偏心率近似为0(存在奇点)，从而导致法化矩阵(HTH)奇异的问题，本文提出基于无奇异变换的广播星历参数拟合算法，该算法通过引入无奇异轨道根数代替经典开普勒根数，推导了空间目标位置矢量对基于无奇异轨道根数的广播星历参数偏导数矩阵，利用变换后的观测方程拟合广播星历参数，并用仿真算例对导航卫星GEO、IGSO的广播星历拟合进行了精度分析。

1 广播星历参数设计

导航卫星的广播星历参数设计为开普勒根数及其扩展参数，包括表示轨道摄动的调和改正系数，外加两个长期项［8］。表1给出了广播星历参数的定义。

需要指出，Ω0对应的是广播星历周历元起始时刻轨道面升交点地理经度［8］，Cus，Cuc，Crs，Crc，Cis，Cic为利用三角函数吸收轨道摄动影响的系数，记为调和项系数。

表1 广播星历参数Table 1 Broadcast ephemeris parameters

2 广播星历参数拟合算法

参考GPS广播星历，真正需要拟合的导航卫星广播星历有15个，即

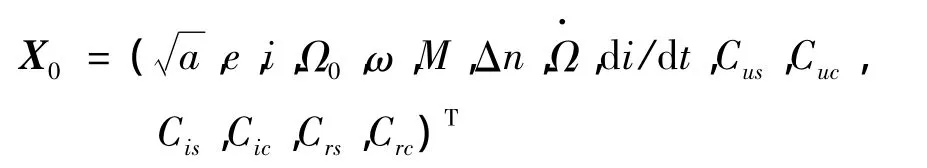
则广播星历参数拟合算法中，相应的状态方程和观测方程为:

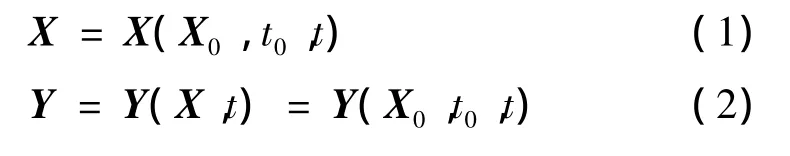
其中:

X0为待估参数向量;

Y为含有m(m≥15)个观测量的观测列向量，一个观测量对应导航卫星在t时刻的一个位置分量。

由于状态方程和观测方程均为非线性方程，因此广播星历参数的估值问题为非线性系统的最小二乘估值问题，需要将非线性方程线性化和迭代求解［9］。

设Xi/0为广播星历参数估值X0在第i次迭代的初值，将方程(2)在X0=Xi/0处展开:

令:

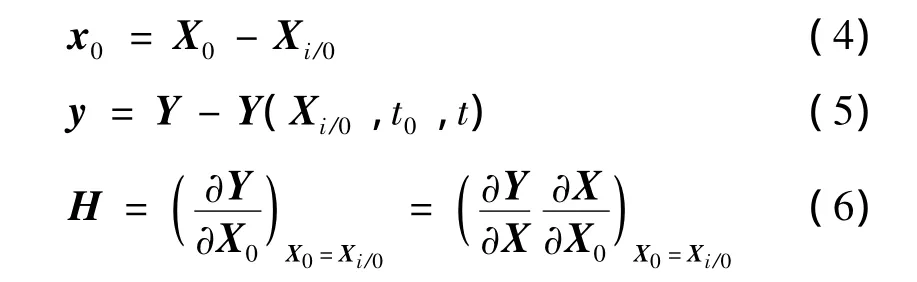
方程(6)的两个列向量偏导数∂a/∂b定义为:

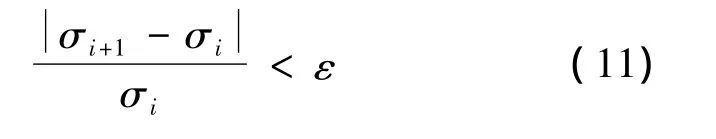
其中:

σ=

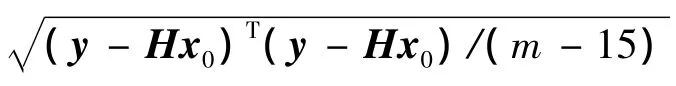
根据最小二乘估值原理，可以得到x0的估值:

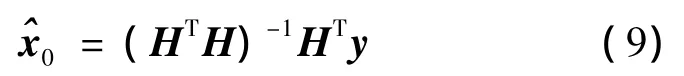
每次迭代结束后，相应的广播星历参数为:

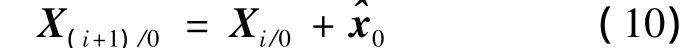
而迭代过程满足公式(11)时停止计算为迭代过程中统计误差;

ε为根据精度要求设定的小量(一般取0．01)。

如果出现小偏心率或小倾角轨道特殊情况，广播星历的最小二乘估计求解需要作相应的处理。事实上，当基本变量为开普勒根数时，位置矢量r对开普勒根数的偏导数为矩阵Λ:

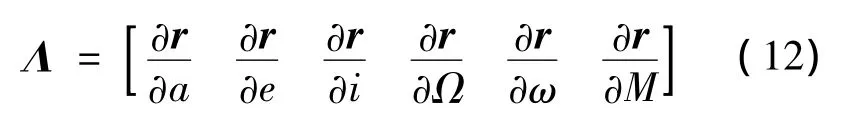
关于列向量 ∂r/∂M和 ∂r/∂ω，不难证明［10－11］:

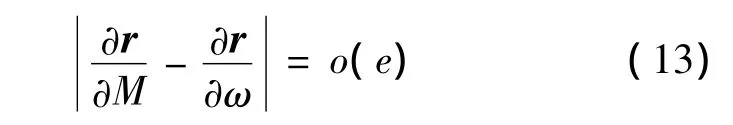
而关于列向量 ∂r/∂Ω 和 ∂r/∂ω，则有

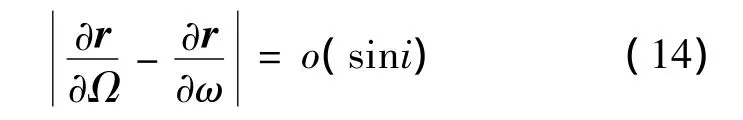
公式(13)，(14)表明矩阵Λ存在两列元素之差为o(e)和o(sin i)的量级，当出现两种奇点的情况e≈0，i≈0或180°，相应的矩阵行列式为0，这将导致法化矩阵非正定，从而破坏了可观测性。对于i≈0或180°的情况，升交点的物理意义不明确，法矩阵HTH接近奇异，导致迭代不收敛。解决这个奇点问题，可以在星历参数拟合前，对导航卫星轨道进行基于轨道倾角的旋转变换，消除轨道倾角出现奇异的情况，具体方法参考文献［5］;对于e≈0的情况，可以采用将卫星近地点角距强制定义为0，进行拟合广播星历，但是拟合精度不好，还可能出现偏心率e为负数的情况。

本文针对e≈0的情况，引入无奇异轨道根数a，i，Ω，ξ，η，λ 替换开普勒根数a，e，i，Ω，ω，M:

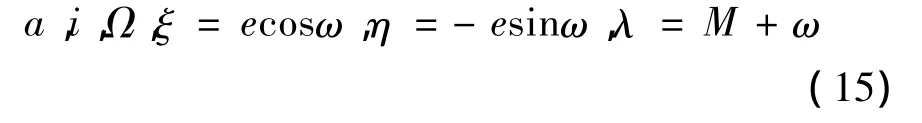
公式(6)中基于无奇异轨道根数的广播星历参数的偏导数矩阵∂Y/∂X公式如下:

其中:

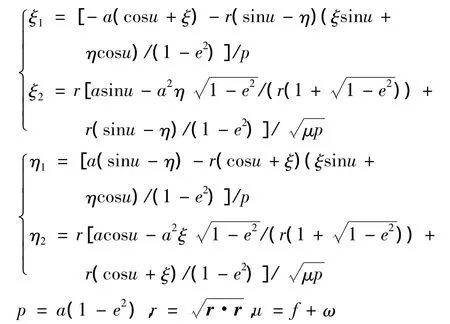
基于无奇异轨道根数X0为:

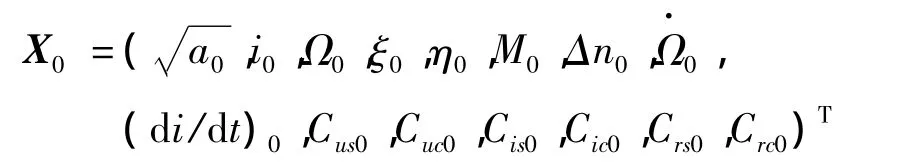
其中，偏导数∂X/∂X0计算公式如下:

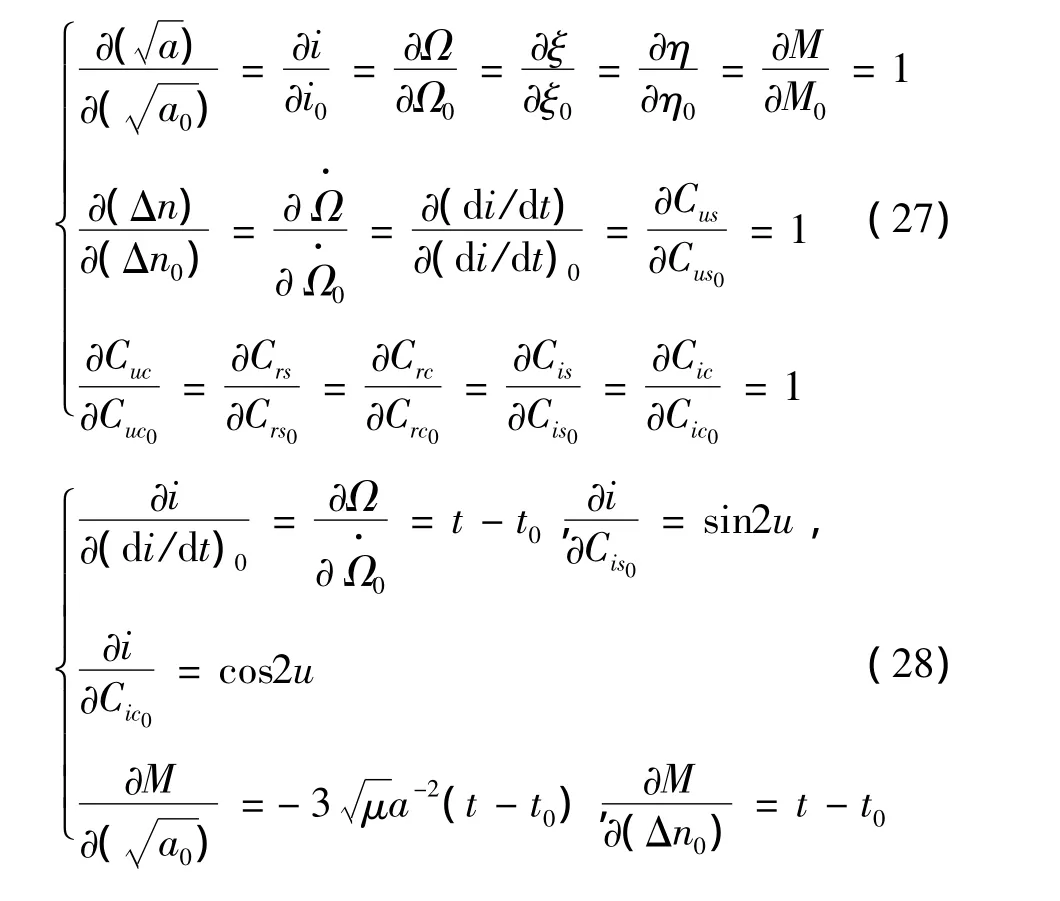
该算法迭代拟合得到ξ，η，λ后，需要归一化到基于开普勒根数的广播星历参数，再对外进行发布，其归一化公式为:

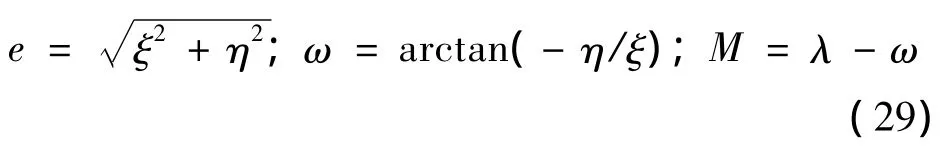
如此处理将保证偏心率e为正数，它的正负性质会转移到卫星的近地点角距ω。

注:无奇异轨道根数归一化到开普勒根数存在精度损失，主要由于在计算近地点角距ω时有舍入误差，精度损失约为o(10－5)。

3 计算结果和分析

广播星历是对卫星轨道的一种数值逼近，因此，广播星历拟合精度是指广播星历对卫星轨道的逼近程度，产生卫星轨道的算法以及卫星轨道本身精度对广播星历拟合精度的影响应该很小，甚至可以忽略不计。对导航卫星的广播星历拟合精度分析正是基于这个原则。

用以产生导航卫星精密星历数据的力学模型为21×21阶地球引力场、日月引力、太阳辐射光压、潮汐摄动、大气阻力摄动等［10］。

GEO(静止轨道)卫星长半轴42164．16km，偏心率0，轨道倾角0°;IGSO(倾斜静止轨道)卫星长半轴42164．16km，偏心率0，轨道倾角约55°。卫星轨道起始历元为:1 Jun 2006 00:00:00．000 UTCG。

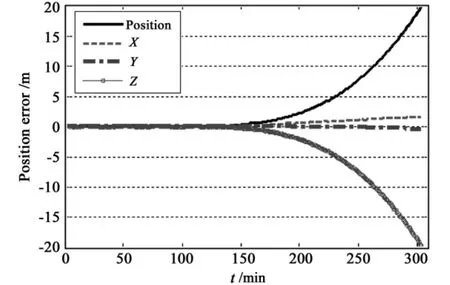
图1 GEO广播星历位置拟合及外推精度Fig．1 Accuracy of position data fitting and extrapolation on GEO

图2 GEO广播星历速度拟合及外推精度Fig．2 Accuracy of velocity data fitting and extrapolation on GEO

图1、图2分别给出了GEO、IGSO卫星在30s数据采样间隔的条件下，5小时弧段长度的广播星历的位置拟合精度与外推精度。前两个小时的精密星历数据用于拟合广播星历参数，广播星历参考历元取其中间时刻:1 Jun 2006 01:00:00．000 UTCG。横坐标为相对于卫星轨道起始历元的时间，纵坐标为位置拟合误差，分别为导航卫星的位置误差(Position)、X方向误差(X)、Y方向误差(Y)和Z方向误差(Z)。图3、图4分别给出了GEO、IGSO卫星广播星历的速度拟合精度与外推精度，横坐标为相对于卫星轨道起始历元的时间，纵坐标为速度拟合误差，分别为导航卫星的速度误差(Velocity)、X方向误差(Vx)、Y方向误差(Vy)和Z方向误差(Vz)。

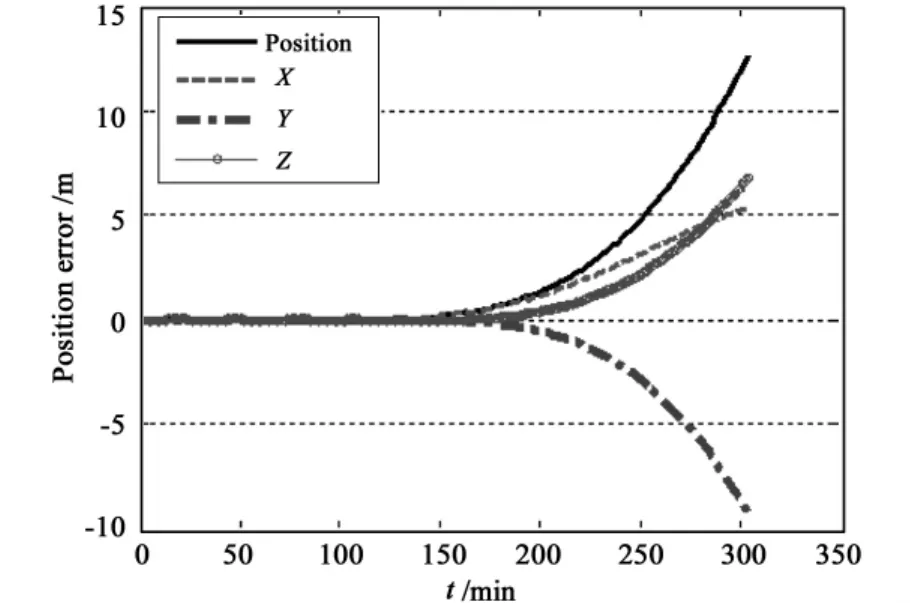
图3 IGSO广播星历位置拟合及外推精度Fig．3 Accuracy of position data fitting and extrapolation on IGSO

由图可知:

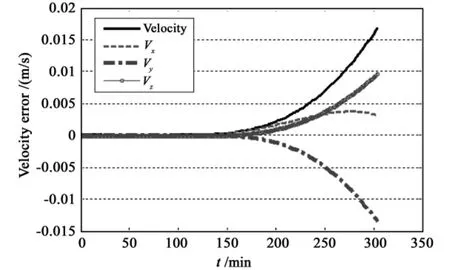
图4 IGSO广播星历速度拟合及外推精度Fig．4 Accuracy of velocity data fitting and extrapolation on IGSO

(1)对于GEO卫星，存在i≈0°的奇点问题，仿真过程中进行了轨道倾角旋转5°处理，广播星历在2小时弧段数据位置拟合误差均方差为0．05m，速度拟合误差均方差为0．0002m/s，位置拟合误差约为等效伪距误差中卫星星历误差(4．2m)［8］的百分之一，可以满足卫星导航定位的精度要求。外推误差随时间迅速增大，外推4小时位置误差达到了20m，速度误差达到了0．026m/s，这将影响卫星导航定位，需要及时更新星历;外推误差主要体现在Z方向上，这是由于GEO星历拟合采用了轨道倾角旋转方法。

(2)对于IGSO卫星，广播星历在2小时弧段数据位置拟合误差均方差为0．048m，速度拟合误差均方差为0．0002m/s，位置拟合误差约为等效伪距误差中卫星星历误差(4．2m)［8］的百分之一，可以满足卫星导航定位的精度要求。外推误差随时间迅速增大，外推4小时位置误差达到了14m，速度误差达到了0．017m/s，这将影响卫星导航定位，需要及时更新星历;外推误差主要体现在Y、Z方向上。

(3)GEO、IGSO卫星，偏心率近似为0，且轨道高度较高，若采用传统广播星历参数的拟合算法，其法化矩阵HTH会接近奇异，无法迭代求解;而采用基于无奇异轨道根数的广播星历参数的拟合算法，可以克服法化矩阵奇异的问题。

需要说明的是:由于采用无奇异轨道根数代替经典开普勒根数形成改进广播星历参数进行迭代求解，最后还要归一化到基于经典开普勒根数的广播星历参数对外发布，在参数转换过程中会导致一定的精度损失。

4 结论

研究广播星历参数拟合算法，不仅对用户导航定位精度的提高具有重要意义，而且对我国卫星导航定位系统广播星历参数设计具有参考价值。文中提出基于无奇异变换的广播星历参数拟合算法，针对导航卫星轨道偏心率近似为0，采用无奇异轨道根数代替经典开普勒根数形成改进广播星历参数进行迭代求解方法，解决了参数拟合过程中法化矩阵(HTH)奇异的问题。通过对GEO、IGSO卫星的仿真结果分析，可以得到好的广播星历拟合精度，满足用户实时导航定位精度要求。但是广播星历的外推精度较差，随着预报时间增加，位置速度误差会迅速增加，这主要是因为本文给出最小二乘拟合算法对于拟合区间外数据的数值逼近效果较差，外推误差较大，还需要进一步改进算法。与文献［5］提出的广播星历参数自主拟合算法比较，本文算法的拟合精度及外推精度都有一定程度的提高，但是计算效率相对较低。

［1］Weber T，Ray J，Kouba J．Review of IGSanalysis products［C］．IGS Network，Data and Analysis Center Workshop，Ottawa，2002．

［2］ 阳仁贵，欧吉坤，闻德保．GPS广播星历误差及定位结果的影响［J］．测绘信息与工程，2006，31(1):1－3．［Yang Rengui，Ou Ji-kun，Wen De-bao．GPS broad-cast ephemeris error and its effect on positioning［J］．Journal of Geomatics，2006，31(1):1－3．］

［3］ 崔先强，焦文海，秦显平．GPS广播星历参数拟合算法的探讨［J］．测绘科学，2006，31(1):25－26．［Cui Xian-qiang，Jiao Wen-hai，Qin Xian-ping．Discussion on the fitting of GPS broadcast ephemeris parameters［J］．Science of Surveying and Mapping，2006，31(1):25－26．］

［4］ 刘光明，廖瑛，文援兰．导航卫星广播星历参数拟合算法研究［J］．国防科技大学学报，2008，30(3):100－104．［Liu Guang-ming，Liao Ying，Wen Yuan-lan．Research on the fitting algorithm of broadcast ephemeris parameters［J］．Journal of National University of Defense Technology，2008，30(3):100－104．］

［5］ 陈忠贵，刘光明，廖瑛，等．广播星历参数星上自主拟合算法［J］．国防科技大学学报，2011，33(3):1－4．［Chen Zhonggui，Liu Guang-ming，Liao Ying，et al．Autonomously updated broadcast ephemeris algorithm［J］．Journal of National University of Defense Technology，2011，33(3):1－4．］

［6］ 石卫平．国外卫星导航定位技术发展现状与趋势［J］．航天控制，2004，22(4):30－35．［Shi Wei-ping．The analysis of development on foreign satellite navigation technology［J］．Aerospace Control，2004，22(4):30－35．］

［7］Zhang K F，Cedric S，Adam M，et al．An investigation of further GNSS in support of research and development of positioning technology in Australia［J］．IEEE Transactions on Aerospace and Electronic Systems，2005，40(4):1159－1165．

［8］ 袁建平，罗建军，岳晓奎．卫星导航原理与应用［M］．北京:中国宇航出版社，2003．

［9］ 文援兰，廖瑛，等．卫星导航系统分析与仿真技术［M］．北京:中国宇航出版社，2009．

［10］ 刘林．人造地球卫星轨道力学［M］．北京:高等教育出版社，1992．

［11］ 刘林．航天器轨道理论［M］．北京:国防工业出版社，2000．