用SAS软件实现均匀设计定量资料的统计分析

胡良平，贾元杰，高辉

在试验中，有时需要考察多个因素，且每个因素有多个水平，可以选用正交设计，如果用正交表安排试验，试验次数还是太多，可以应用均匀设计。均匀设计是用最少的试验次数取得关于总体的尽可能充分的信息，它是只考虑试验点在试验范围内均匀散布的一种试验设计方法。该设计方法较相同规模的正交设计而言，大大降低了试验次数。

1 正交设计与均匀设计基本特点的比较[1]

当试验因素较多而每个因素又有较多的水平时，通常会采用正交设计。正交设计特点是在全部因素所构成的空间内其试验点具有“均匀分散性”和“整齐可比性”。“均匀分散”可使所选取的少量试验点均匀地散布在所考察的范围内，各试验点具有较好的代表性，以此减少试验次数；“整齐可比性”可使试验结果的分析来得方便，便于找出主要因素和次要因素及最佳水平组合（最优试验条件）。但是，为了达到“整齐可比”的目的，试验点的数目必然较多，试验因素皆取同水平的情况下，通常其因素的水平组合数（即所选用的正交表的行数）至少为水平数的平方。且当试验因素的个数和水平数都大于 5 时，试验次数就会剧增。均匀设计可以克服正交设计的这个弱点。

均匀设计舍弃了正交设计中的整齐可比性，让试验点在其试验空间范围内充分地“均匀分散”。这样每个试验点将具有更好的代表性，而试验点的数目可大幅度地减少，试验次数（试验点数 × 各试验点上重复试验次数）也就相应地大量减少。在最节省样本量的均匀设计中，每个因素的每个水平只出现一次，若不做重复试验，试验次数与水平数相等。例如，一个 8 水平的试验，正交设计至少需要 64 次试验，而均匀设计只需要 8 次试验，在科研经费不足的情况下均匀设计可以大大降低成本，达到一个较好的效果。均匀设计其试验次数少，且因素的水平可以适当调整，故它在寻找最佳试验条件、最佳配比等方面是比较有力的工具。

2 均匀设计表的使用

均匀设计与正交设计相似，也是通过数学方法设计出一套均匀设计表，供研究者选用。均匀设计表的代号为其中“U”表示均匀设计，“n”表示表的行数，即表示全部因素的 n 种水平组合，“q”表示每个因素有 q 个水平，“s”表示该表的列数。U 的右上角加“*”和不加“*”代表两种不同的均匀设计表，通常加“*”的均匀设计表有更好的均匀性，但表 Un比能安排更多的因素。如表示此均匀设计表有 6 行（代表因素的 6 种水平组合），试验中有 6 个因素，每个因素有 6 个水平；而表最多可以安排 4 个因素的试验，即表最多只能安排 [s/2]+ 1，这里 [s/2] 表示不超过 s 的最大整数。故当因素数 s较大，且超过的使用范围时，可使用 Un表。

2.1 均匀设计表的特点

①在同类均匀表中，行数最少的均匀表为因素的水平数；②均匀设计表任两列组成的试验方案一般并不等价，每一个均匀设计表必须有一个附加使用表；③当因素的水平数增加时，均匀表的行数按水平数的增加量增加。如当水平数从 7 水平增加到 8 水平时，均匀表的行数 n 从 7 增加到8 或从 14 增加到 16。

2.2 均匀设计表的选择原则

①应根据要考察的因素个数和水平数选择合适的均匀设计表；②当试验中的因素个数少于均匀设计表中最多可安排的因素个数时，为确保不同因素水平的组合所对应的试验点在空间分布均匀，每个均匀设计表都配有一个使用表供查用。

2.3 均匀设计表的使用要点[2]

2.4 均匀设计表的应用步骤[3]

3 均匀设计应用的注意事项[4-5]

均匀设计可考察的水平数较多，故利用均匀设计对较多的影响因素进行初筛，快速划定考察范围，再用正交设计或析因设计进行较为仔细地研究，可以达到较好的效果。运用均匀设计筛选最优试验条件关键点在于指标的选择。一般可选取比较重要的一、二项指标作为主要评价指标；水平数与因素数应有适当的比例，至少水平数大于因素数的 2 倍以上，才有利于正确使用回归分析处理试验资料。因为若水平数设计得不合理，比如，与因素数相等、甚至少于因素个数，此时，由均匀表所决定的试验点在高维空间中显得非常“稀疏”，据此建立的回归方程是很不稳定的；重视回归分析，选行数 n 稍大的均匀设计表，在已知实际背景时少用多项式，在采用多项式时尽量考虑二次的，尽可能避免使用三次或四次多项式拟合资料；当回归方程完全拟合均匀设计定量资料时，可能不是好事，属于“过拟合”，提示：有必要选择行数较多的均匀表安排试验并重做试验。

4 如何用 SAS 软件处理均匀设计一元定量资料

在三七的提取工艺中根据查找文献及预试验的结果选定试验因素，选择乙醇浓度 A，乙醇用量 B，回流时间 C，回流温度 D，浸泡时间 E，5 个因素进行考察，以三七提取的收率作为考察的指标，将各因素考察范围分为 11 个水平，数据见表 1。拟挑选出最优试验条件。

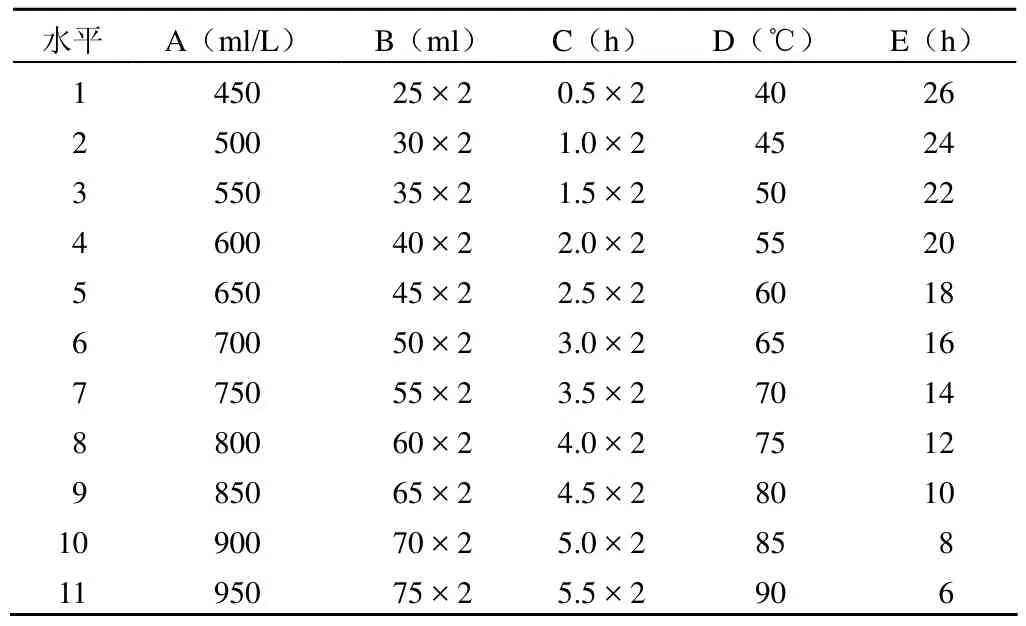
表 1 三七提取工艺试验因素水平

设计需求分析与计算的 SAS 实现：①研究者根据文献或预试验的结果选定 5 个试验因素分别是“乙醇浓度 A，乙醇用量 B，回流时间 C，回流温度 D，浸泡时间 E”，每个因素各有 11 个水平。如果选用正交设计至少需要112= 121 次，试验次数太多，一般研究者很难承受。试验次数最少的均匀设计只需 11 次试验，可较好实现节约试验经费和时间的目的。

②试验共有 5 个因素，每个因素均有 11 个水平，根据均匀设计表可以选择 U11(116)见表 2。

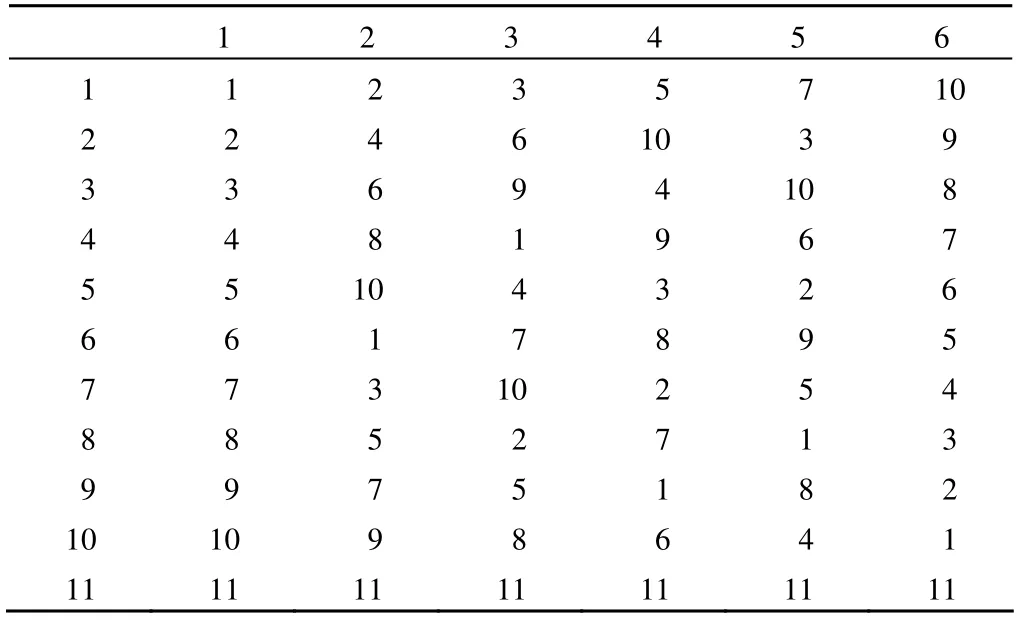
表 2 U11(116)均匀设计表

U11(116)的使用表

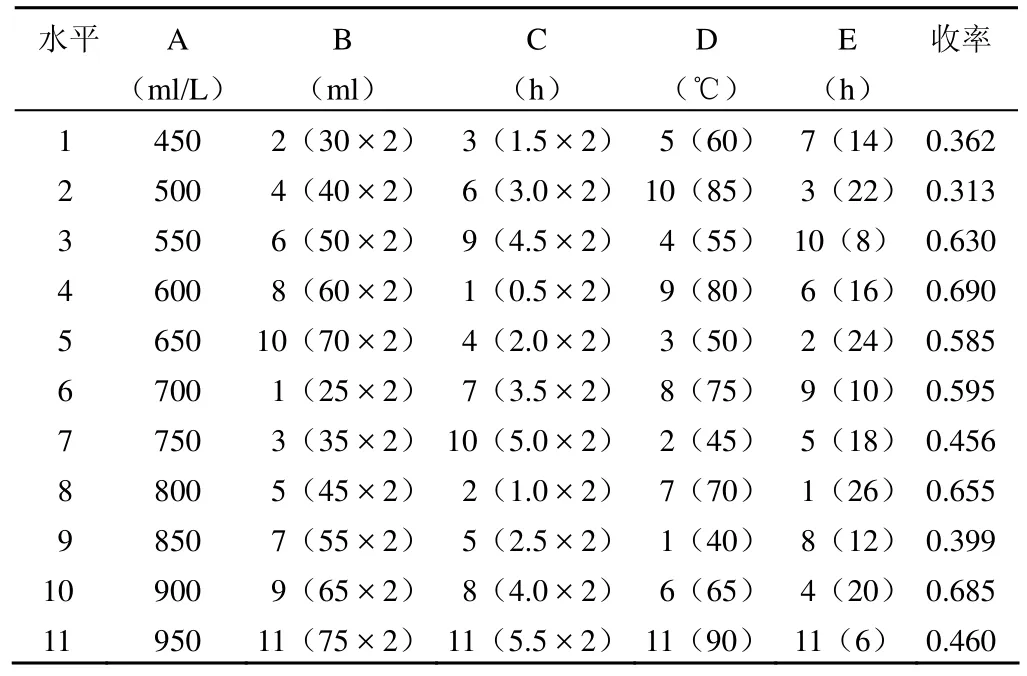
表 3 三七提取试验均匀设计安排表 U11(115)

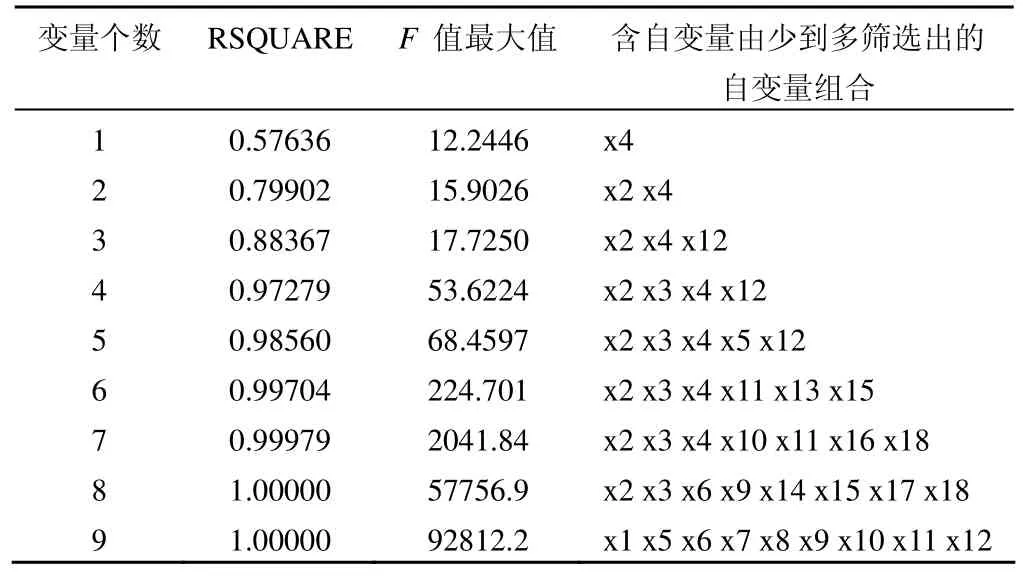
表 4 各变量全排列组合回归分析 F 值情况

从以上结果可以看出变量个数为 9 时 F 值最大（F =92812.2），选取这个变量组合筛选出的自变量 x1、x5、x6、x7、x8、x9、x10、x11、x12 建立多重线性回归方程。

⑤将筛选出的自变量进行回归分析，建立回归方程。SAS 程序如下：

data junyun; /*数据步*/input x1 x2 x3 x4 x5 y;x1=(x1-700)/50;x2=(x2-100)/10;x3=(x3-6)/1;x4=(x4-65)/5;x5=(x5-16)/2;x6=x1**2;x7=x2**2;x8=x3**2;x9=x4**2;x10=x5**2;x11=x1*x2;x12=x1*x3;x13=x1*x4;x14=x1*x5;x15=x2*x3;x16=x2*x4;x17=x2*x5;x18=x3*x4;x19=x3*x5;x20=x4*x5;cards;450 60 3 70 14 0.362 500 80 6 40 22 0.313 ods html; /*第 1 步*/proc reg data=junyun;model y= x1 x5 x6 x7 x8 x9 x10 x11 x12 / r p vif collin collinoint;run;proc princomp data=junyun out=pc2 prefix=z; /*第 2 步*/var x1 x5 x6 x7 x8 x9 x10 x11 x12;run;proc reg data=pc2; /*第 3 步*/model y=z1-z9/ r p vif stb;run;quit;

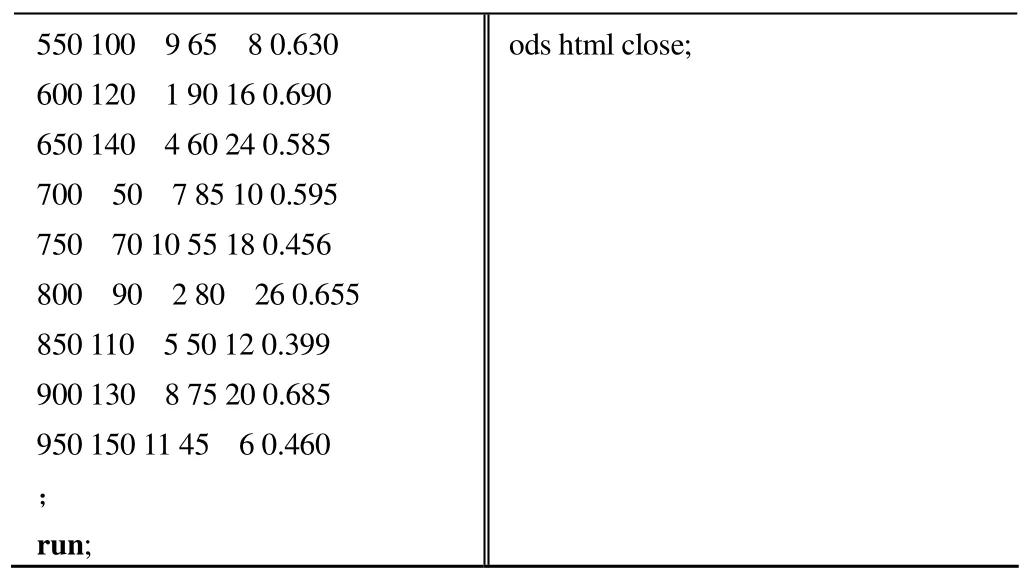
550 100 9 65 8 0.630 600 120 1 90 16 0.690 650 140 4 60 24 0.585 700 50 7 85 10 0.595 750 70 10 55 18 0.456 800 90 2 80 26 0.655 850 110 5 50 12 0.399 900 130 8 75 20 0.685 950 150 11 45 6 0.460；run;ods html close;

数据步中 x1 ～ x5 的数量级相差较大，将这五个变量进行标准化变换。第 1 步是将筛选出的 9 个变量（含派生出的新变量，即交叉乘积项和平方项）进行回归分析，并使用r、collin 和 collinoint 选项进行残差分析及共线性诊断。这部分结果如下：

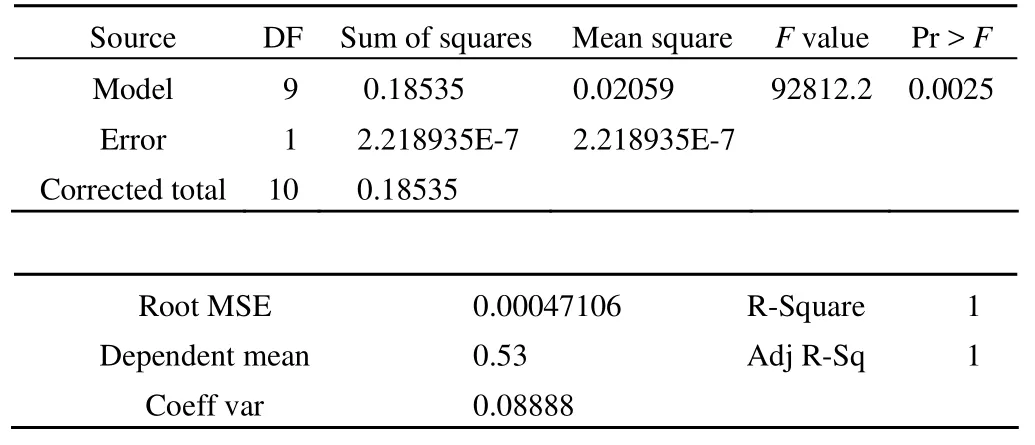
Analysis of variance

值得注意的是：当 F 值很大时，SAS 系统给出的 P 值是不正确的，正确的结果为：P < 0.0001

这是对回归方程进行方差分析，其拟合效果较好（F =92812.2，P = 0.0025 < 0.05，R2= 1）。

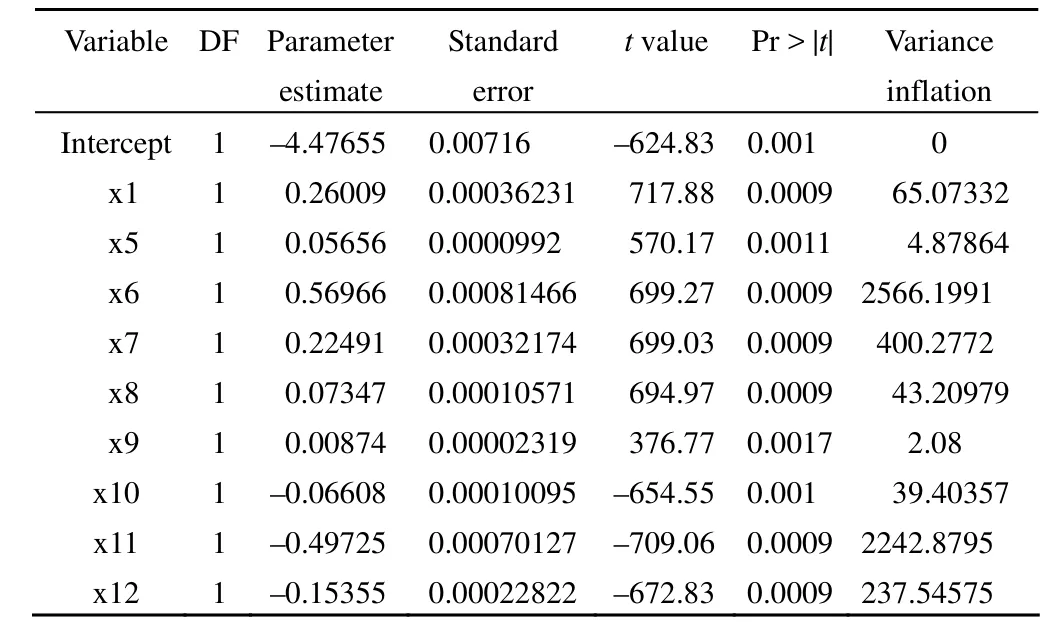
Parameter estimates

这是多重线性回归分析参数估计的结果。截距项及各变量的系数与 0 的差异都有统计学意义（P < 0.05）。由最后一列“方差膨胀因子”可看出，除 x5 与 x9 与其他自变量间不存在共线性外，其他自变量之间均存在严重的多重共线性。由 collin 和 collinoint 两个选项产生的多重共线性诊断结果（篇幅很大，从略）与方差膨胀因子诊断结果基本一致。

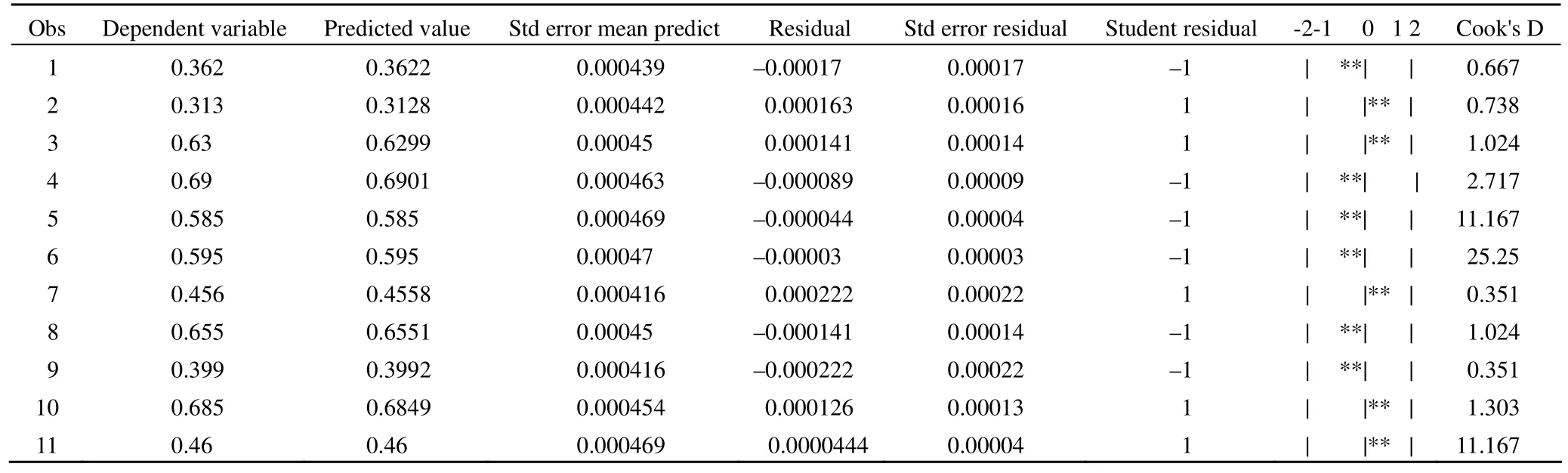
Output statistics

这是对回归方程作残差分析的结果，没有发现异常点。由于变量间存在严重的多重共线性，故第 3 步对 9 个自变量进行主成份分析。主要输出结果如下：

因篇幅所限，相关系数矩阵的特征值、贡献率、累积贡献率和特征向量均从略。根据给出的特征向量可以写出由标准化变量所表达的各主成份的关系式，可得到下式：

程序中的第 3 步将这 9 个主成份作为新自变量进行回归分析，并输出回归方程的标准化回归系数。主要输出结果如下：

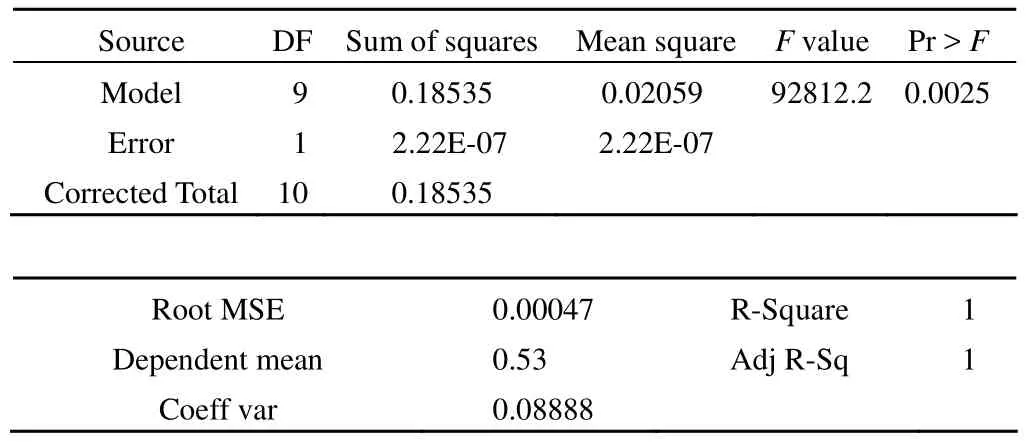
Analysis of variance

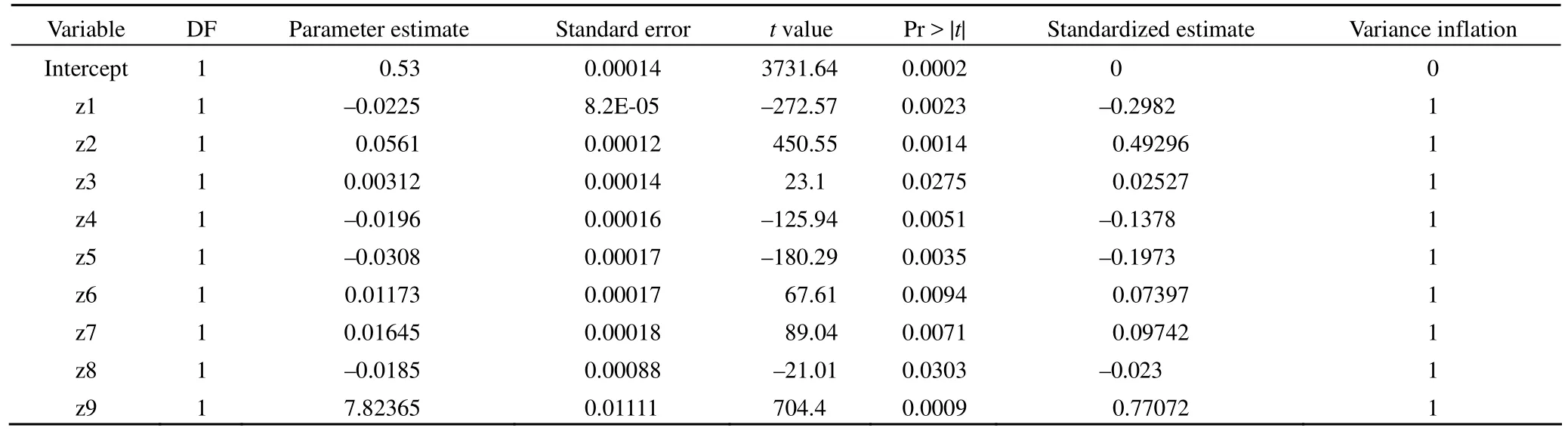
Parameter estimates

模型总体较好地拟合了数据（F = 92812.2，P = 0.0025 <0.05，R2= 1）。截距项及 z1 ～ z9 的系数与 0 的差异均有统计学意义。回归方程如下：

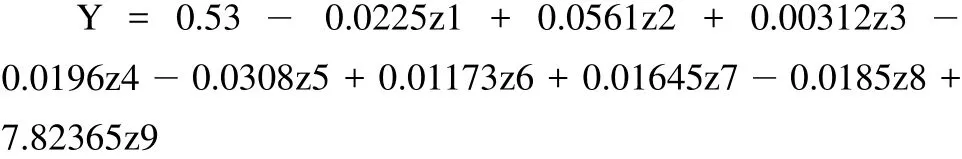
将 z1 ～ z9 的表达式回代到上面回归方程，得：

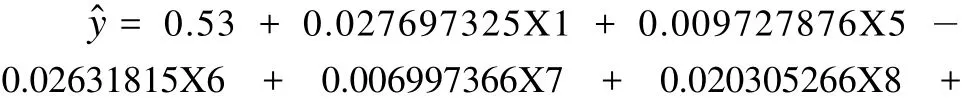
将上面回归方程中标准化后的 X 还原为原始的 x，得：

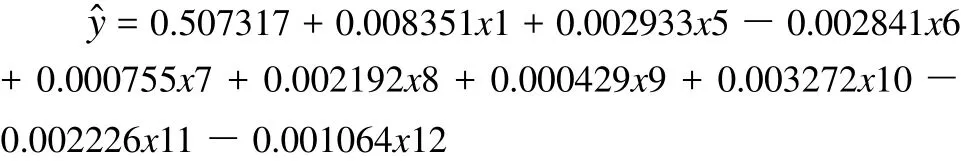
将 5 个因素及其派生变量的各种水平取值组合代入回归方程找出最佳试验条件，程序太长这里不列出。结果是当x1 取 900，x2 取 50，x3 取 1，x4 取 40，x5 取 26 时，y收率达到最大为 74.193%。

回顾整个过程，得出的回归方程很好地拟合了数据（F = 92812.2，P = 0.0025 < 0.05，R2= 1），且残差分析的结果为因变量的值和预测值相差非常微小，几乎可以说这个超平面穿过每一个试验点（这在统计学上被称为“过拟合”），但最终得到的这个结果可以作为定论吗？答案是否定的。均匀设计的特点是因素多、水平多、试验点少，满足均匀分散性丧失了整齐可比性，仅仅选取了 11 个具有代表性的试验点（方程中却有 9 个变量），其结果十分不稳定。只要增加一个试验点其最终结果就可能会发生很大改变，故最后结果不能代表所有变量在五维空间中的整体变化趋势，要想使试验结果达到稳定必须增加试验点，并在各试验点上进行足够多次数的重复试验，但这样做必然使试验次数成倍增加，丧失了均匀设计的初衷和意义。因此，均匀设计只能作为探索性分析的有效工具，得出的结果仅作为初步筛选出有意义的因素和交互作用项，为后续的深入研究奠定必要基础，而不能作为整个试验的定论。也就是说，当一个试验有很多因素及水平时，我们可以先运用均匀设计找出对因变量影响较大的因素，缩小需考察的因素范围和水平的个数，继而再应用析因设计或正交设计，进一步考察因素的效应及其交互效应，这样才能得到具有高度重现性的确定性结论，得出的最终结果才是有意义的（经得起时间和实践的检验）。

[1] Fang KT, Ma CX. Orthogonal and uniform experimental design.Beijing: Science Press, 2001:35-39, 83-85. (in Chinese)方开泰, 马长兴. 正交与均匀试验设计. 北京: 科学出版社, 2001:35-39, 83-85.

[2] Li YY, Hu CR. Experimental design and data processing. Beijing:Chemical Industry Press, 2005. (in Chinese)李云雁, 胡传荣. 试验设计与数据处理. 北京: 化学工业出版社,2005.

[3] Feng XL. Experimental designs methods in science research--Uniform design. Train Technol. 2004, 25(2):98-100. (in Chinese)冯新泸. 科学研究中的试验设计方法——均匀设计. 训练与科技,2004, 25(2):98-100.

[4] Yuan Y, Wang Y, Wang XC. Key issues of uniform design in pharmaceutical research. Chin Hosp Pharm J, 2003, 23(7):440-441.(in Chinese)袁勇, 王阳, 王新春. 均匀设计法在药物制剂研究中应注意的问题.中国医院药学杂志, 2003, 23(7):440-441.

[5] Guo DX, Qiu LX, Zhang MD. Uniform design method and it's application. Journal of Mathematical Medicine, 2005, 18(1):69-71. (in Chinese)郭东星, 仇丽霞, 张满栋. 均匀设计方法及其应用. 数理医药杂志,2005, 18(1):69-71.