紧凑型混合堆径向几何尺寸与发电成本的优化

陈美霞, 刘成岳, 吴 斌

(1.合肥工业大学 电子科学与应用物理学院,安徽 合肥 230009;2.中国科学院 等离子体物理研究所,安徽 合肥 230031)

紧凑型聚变裂变混合堆又称紧凑型混合堆,与传统的托卡马克反应堆相比,是一种新的概念设计,具有安全、高效等特点,有利于实现聚变能商业化。由于其中心螺管尺寸较小,在稳态时通过非自感来驱动等离子体电流,具有较小的环径比,可以获得较大的拉长比和较高的比压值。同时由于其中心螺管尺寸较小,使得环向场线圈也较小,可以减小反应堆的体积和结构成本。因此,该混合堆的研究具有重要的理论和现实意义[1-3]。

聚变研究是一项复杂的系统工程,必须建立相应的装置开展实验研究。而聚变能研究的目标是设计制造可靠、安全、高效、环境相容性好的大规模商业聚变电站。发展聚变电站,要求具有高的安全性和好的环保性,此外,其经济性一直是概念设计与工程设计阶段考虑的重要因素[4-5]。

1 紧凑型混合堆及发电成本模型

1.1 混合堆构成及物理原理简介

紧凑型混合堆由聚变堆芯及其辅助设施(如环向场、极向场线圈,电源系统,加料排灰系统,等离子体诊断系统,传热回路、加料卸料等子系统)、包层(含屏蔽包层和工作包层)等组成,如图1所示[6]。其中极向场是激发、加热等离子体,驱动等离子体电流,维护等离子体平衡位形的重要部件。极向场线圈和等离子体环构成一个变压器,通过变压器效应驱动等离子体电流。由于等离子体电阻的存在产生欧姆加热,使等离子体温度升高。

图1 聚变裂变混合堆结构示意图

极向场线圈产生的极向磁场用于等离子体的平衡控制,磁约束等离子体力学平衡条件为[7]:

其中,j、B及p分别表示等离子体内部任一点的等离子体电流密度、磁感应强度和压强。(1)式表明等离子体内部任意一点压强梯度被磁力平衡。

环向场线圈产生强环向磁场与等离子体电流产生的较弱极向磁场叠加使磁力线绕磁轴旋转,将载流等离子体约束在一个轴对称的环形真空室中,环向场系统主要是保障环向等离子体电流稳定放电。

混合堆径向由内向外包括中心螺管、环向场线圈、真空室、内屏蔽层、内包层、等离子体区、外包层及外屏蔽层等,如图2所示。位于装置中心的中心螺线管在纯欧姆加热下是等离子体放电的关键部件,其主要功能是提供等离子体放电过程中所需的伏秒消耗。紧凑型混合堆系统最有特色的设计是多功能包层。以等离子体所在的位置来划分,包层分为内包层和外包层。内包层主要承担氚增殖,外包层除具备内包层功能外,还要实现增殖裂变燃料、嬗变长寿命高放废物(包括锕系元素和裂变产物)的功能。等离子体大半径[8]可表示为:

其中,R为等离子体大半径;R coil为中心柱到环向场线圈外侧的距离;δBS为内包层及内屏蔽层厚度;a为等离子体小半径,如图2所示。

图2 混合堆径向几何尺寸示意图

1.2 发电成本计算模型

评价任何一种能源的效益,除了技术先进、环保可行外,最具竞争力的还是经济指标。目前评价聚变电站经济价值的通用指标是电站全寿期平准化发电成本(Levelized Cost o f Electricity),简称为发电成本(COE)[4,9],为年总费用与年实际发电量之比,其单位通常采用 mill/(kW ·h)。COE越小,则表明其经济价值越高,商业竞争力越强。

目前,计算COE的模型还在不断完善,本文采用的COE模型为[10]:

其中,C AC为年投资成本,C AC=T CC f FCR,T CC为总建造成本,f FCR为年固定费用率;C F为运行起始年的年燃料成本;CO&M为运行起始年的年运营与维护成本;C SCR为运行起始年的年定期部件更换与更新成本;CR&D为年研发成本;CD为年净化与退役成本;y为年通货膨胀率;Y为订货至交货周期;P E为电站输出净电功率;p f为电站平均可用率。

2 发电成本优化分析

在发电成本优化分析的计算过程中,考虑到紧凑型混合堆工程可行性,在标准环径比聚变裂变混合堆物理参数的基础上,在反应堆径向的大半径、小半径分别不变及大小半径之和不变时,对紧凑型混合堆中心螺管尺寸分别进行优化分析,以寻找紧凑型混合堆发电成本最优化的设计参数。

2.1 大半径不变时的优化分析

表1所列为标准环径比聚变裂变混合堆物理设计参数[6,11],以此为基础,在保持聚变裂变混合堆的大半径4.00 m不变的前提下,对其中心螺管的宽度进行优化,通过聚变系统分析程序可以算出总建造成本 TCC、聚变功率 P F、发电成本COE随小半经a的变化情况以及COE随环径比A的变化情况,如图3所示。

由图3可知,TCC和PF在小半径a从1.00 m增加到1.38m时随着a的增加而增加,此后均随着a的增加而下降;COE在a从1.00 m增大到1.45 m时,随着 a的增大而降低,在 1.45～1.50 m之间几乎不变,而从1.50 m后又开始增大;COE在环径比A从4.00降到2.76时,随着A的降低而降低,当 A在2.76～2.67之间时COE几乎不变,然后随着 A的进一步降低COE反而升高。由此找到在大半径4.00m不变时的最佳设计参数是:小半径1.50m,环径比2.67,最优发电成本COE为20.514 mill/(kW·h)。

表1 标准环径比聚变裂变混合堆的设计参数

图3 T CC、P F、COE随a的变化及COE随A的变化

2.2 小半径不变时的优化分析

如果保持紧凑型混合堆的小半径1.00 m不变,对其中心螺管的宽度进行优化,同样可以算出TCC、PF、Pwn及COE随 R的变化情况。由图4可知,随着 R 的增加,T CC、P F、P wn也随之增加,但COE随着R的增加而降低;由于小半径1.00 m不变,所以COE随环径比A的变化情况与图4d完全相同。在小半径1.00 m保持不变的情况下,随着大半径增加,环径比也在增加,从而堆体尺寸增加,磁体和极向场线圈体积和质量增加,导致直接成本增加,最终引起总建造成本的上升;同时,随着大半径增加,聚变功率、热功率、毛电功率和中子壁负载也增加,最终使得TCC增加,但COE下降,在大半径为 4.00 m时,电价最优为21.794mill/(kW·h)。因此,在小半径1.00 m不变时的最佳设计参数为:大半径4.00m,环径比4,最优电价COE为21.794m ill/(kW·h)。

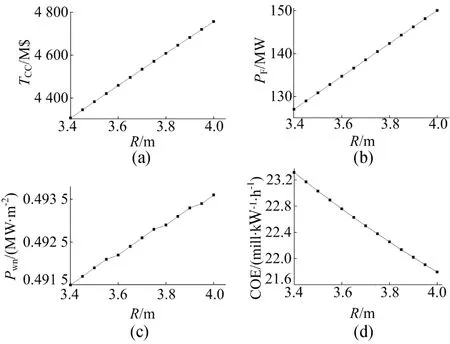
图4 T CC、P F、P wn及 COE随 R的变化

2.3 大小半径之和不变时的优化分析

在大小半径之和不变情况下,对标准环径比聚变裂变混合堆中心螺管尺寸进行优化分析,寻找发电成本最优化的设计点,计算结果如图5所示。可以看出,P wn随着 a的增大而减小;P F在 a从1.00 m增加到1.13m时是随之增加的,而后随着a的增加而降低;TCC开始时随着a的增加也随之增加,在a增加到1.05 m时 TCC达到最大值,此后随着a的增加T cc依次降低;COE在a从1.00m增加到1.22m时降到最小值21.204m ill/(kW·h),再继续增加小半径a,COE反而略有上升。

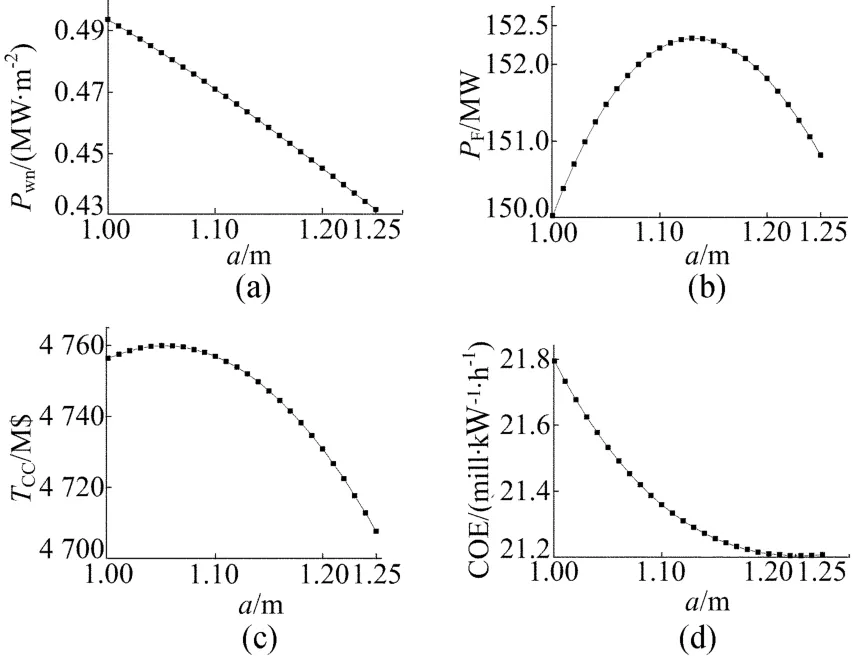
图5 P wn、P F、T CC及 COE 随 a的变化

由于大半径与小半径之和保持不变,当中心螺管尺寸减小,小半径增加时大半径相应降低,由此得到P wn、P F、Tcc以及COE 随R的变化情况,如图6所示。可以看出P wn随着R的减小而减小;P F在R从4.00m减小到3.87m时是增加的,而后随着R的减小而降低;TCC开始时随R从4.00 m减小而增加,在R降到3.95m时 TCC达到最大值,此后随着R的减小T CC依次降低;COE在R从4.00m减小到3.78m时降到最低值21.204 mill/(kW·h),再继续降低R,COE反而略有上升。

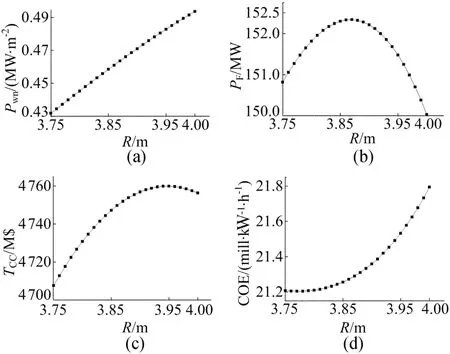
图6 P wn、P F、T CC及COE 随 R 的变化

综合以上优化计算分析得到大、小半径分别不变和大小半径之和不变3种情况下紧凑型混合堆发电成本的优化情况,见表2所列。

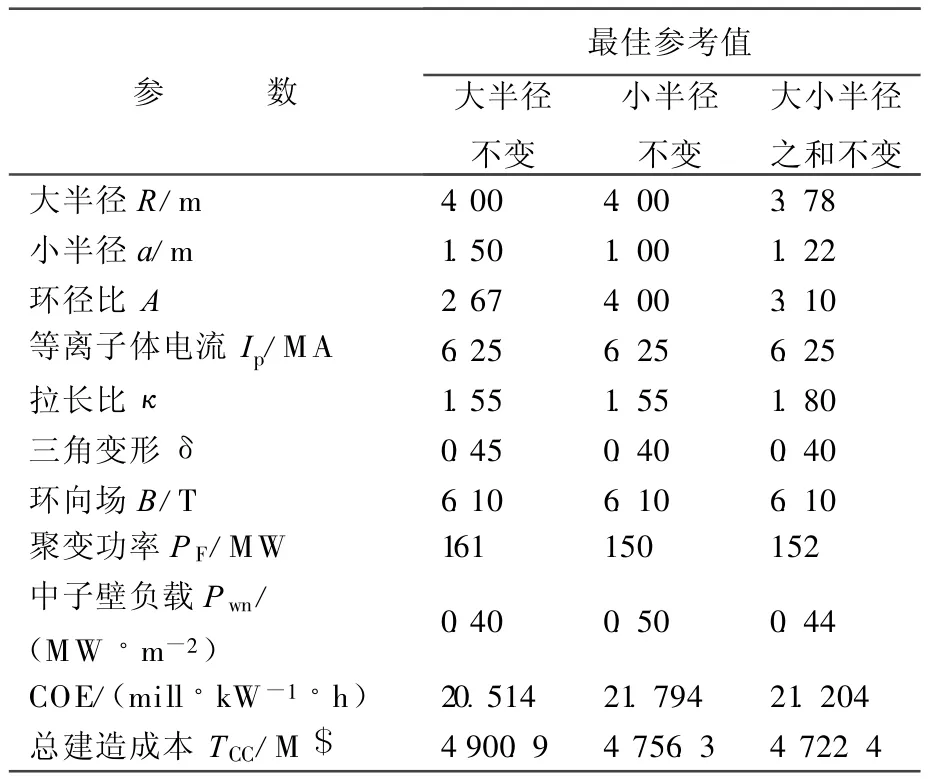
表2 3种情况下混合堆的优化参数值

可以看出大半径不变时的聚变功率最高,总建造成本略高,但中子壁负载和发电成本均最低,由此得出紧凑型混合堆的最佳设计参数即为大半径不变情况下的优化参数,即大半径4.00m,小半径1.50m,环径比2.67,聚变功率约161 MW,中子壁负载约 0.40 MW/m2,最优 COE为20.514mill/(kW·h)。

3 结束语

本文介绍了紧凑型混合堆的概念,并就紧凑型混合堆的径向几何尺寸对发电成本的影响进行了优化分析,从而获得最优化的设计点,即大半径4.00 m,小半径1.50 m,环径比 2.67,聚变功率约161MW,中子壁负载约0.40 MW/m2,得最优COE为20.514mill/(kW·h)。优化的模拟结果对今后混合堆的经济学分析及未来混合堆的建堆设计都有一定的参考价值。

[1]黄德所,吴宜灿,储德林,等.聚变驱动次临界堆经济性分析[J].核科学与工程,2004,24(2):184-192.

[2]Tobita K,Nishio S,Sato M,et al.Concept of compact low aspect ratio DEMO Reactor,SlimCS[C]//Proc of 21th IAEA Fusion Energy Conference,Chengdu,China,16-22 October 2006:1-8.

[3]刘成岳,陈美霞,宋逢泉.EAST托卡马克拉长位形演化的数值模拟[J].合肥工业大学学报:自然科学版,2010,33(5):770-772,782.

[4]Tokimatsu K,Okano K,Yoshida T,et al.Study of design parameters form inim izing the cost of electricity of tokamak fusion reactor[J].Nu clear Fusion,1998,38(6):885-902.

[5]A conceptualstudy of commercial fusion pow er plants:Final Report of the Eu ropean Fusion Power Plan t Conceptual Study(PPCS),EFDA-RP-RE-5.0[R/O L].European Fusion Development Agreement,2005:1-24[2010-07-10].http://www.efda.org/dow nloads-divers/ppcs.

[6]吴宜灿,柯 严,郑善良,等.聚变驱动次临堆FDS概念设计研究[J].核科学与工程,2004,24(1):72-80.

[7]W esson J.Tokam ak s[M].Oxford:Clarendon Press,1987:109-111.

[8]储德林.聚变驱动次临界系统 FDS堆芯物理研究[D].合肥:合肥工业大学,2004.

[9]黄德所.聚变驱动次临界堆经济性研究[D].合肥:中国科学院等离子体物理研究所,2006.

[10]邱励俭.聚变能及其应用[M].北京:科学出版社,2008:399-409.

[11]Wu Bin.Introduction of fusion driven subcritical system p lasma design[J].Fusion Engineering and Design,2003,66/67/68:181.