A New Class of p-Ary Quadratic Bent Functions

(College of Mathematics and Statistics, South-Central University for Nationalities, Wuhan 430074, China)

1 Introduction

Bent functions were first introduced by Rothaus in 1976 as an interesting combinatorial object[1]and they have been extensively studied for their important applications in coding theory, cryptography and sequence designs. In 1985, Kumar, Scholtz and Welch generalized bent functions to the case of an arbitrary finite field[2]. Precisely, letf(x) be a function mapping Fpnto Fp. The Walsh transform off(x) is defined by

(1)

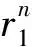
Recently, weakly regular bent functions were shown to be useful for constructing certain combinatorial objects such as partial difference sets, strongly regular graphs and association schemes (see Ref[4,5] ). This justifies why the classes of (weakly) regular bent functions are of independent interest. The quadratic bent functions have been comprehensively studied and they are shown to be weekly regular in Ref[6].

are studied in this paper, and they are proved to bep-ary bent functions whenmis odd ormis even buta(pn-1)/(p+1)≠1. Notef(x) is weekly regular since it is quadratic, and hence it can be used to construct partial difference sets, strongly regular graphs and association schemes[4,5].

The remainder of this paper is organized as follows. Section 2 gives some definitions and preliminaries. Sections 3 proves the main result and section 4 concludes the studies.

2 Preliminaries

whereaij∈Fp. The rankrof the quadratic formf(x) is defined as the codimension of the Fp-vector space

W={z∈Fpn|f(x+z)=f(x) for allx∈Fpn},

namely, |W|=pn-r. The quadratic formf(x) mapping Fpnto Fpis nondegenerate if its rank is equal ton. For more details about quadratic form over finite fields, the reader is referred to Ref[3].

The following lemma is the proposition 1 in Ref[6] and it will be used to prove the main result in this paper.

Lemma1[6]Any quadratic formf(x) mapping Fpnto Fpis bent if and only if it is nondegenerate. Moreover, all quadraticp-ary bent functions are weakly regular.

3 Main theorem and its proof

(2)

Theorem1 Letf(x) be the function defined in Eq. (2). Then,f(x) is a bent function ifmis odd ormis even buta(pn-1)/(p+1)≠1.

ProofLetrbe the rank off(x). Then,pn-ris the number of the variablez∈Fpnsuch that

f(x+z)=f(x)

(3)

for allx∈Fpn. Eq. (3) holds if and only if

i.e.,

(4)

If Eq.(4) holds for allx∈Fpn, then

apm+1zp2-(γdp+γdpm+1)zp+az=0.

(5)

and

(6)

By Eq.(5), one has

i.e.,

which leads to

Thus, Eq.(5) implies Eq.(6) and the number of solutionszto Eq.(3) is the same as that to Eq.(5). Note:

apm+1zp2+az=0.

(7)

Ifz≠0, Eq.(7) is equivalent to:

zp2-1=-(a-1)pm+1-1.

(8)

Letαbe a primitive element of Fpnand

a-1=αi0.

(9)

for somei0∈{0,1,…,pn-2}. Then, Eq.(8) is equivalent to the equation of the unknownt∈{0,1,…,pn-2}:

which holds if and only if

(10)

The congruence (10) has solutions intif and only if

(11)

1(mod 2).

Thus, in this case Eq.(11) can not hold and Eq.(10) has no solutions int.

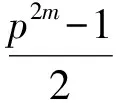
gcd(p2-1,pm+1-1)=p-1.

Thus

Moreover,a(pn-1)/(p+1)≠1 implies thatp+1 does not dividei0, wherei0is defined in Eq.(9). Therefore,

i.e.,p2-1 does not dividei0(pm+1-1). Thus, Eq.(11) can not hold and Eq.(10) has no solutions int.

Combining the above two cases, one can conclude that ifmis odd ormis even buta(pn-1)/(p+1)≠1,z=0 is the only one solution of Eq.(5) in Fpn. Therefore, the rank off(x) isnandf(x) is nondegenerate. By Lemma 1,f(x) is a bent function and the proof is finished.

4 Conclusion

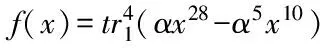
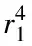
Sf(b)Frequency9339(-1+3i)2249(-1-3i)224

Example2 Letn=6,m=3,p=3 andαbe a primitive element of F36with the minimal polynomialx6+x5+2. Leta=1,γ=α. The bent function isf(x)=

表2 函数的Walsh变换Sf(b),b∈F36Tab.2 Walsh Transform Sf(b) of f(x)=t(x82-α14x28)，b∈F36

[1] Rothaus O S. On bent functions[J]. J Comb Theory A, 1976, 20(3): 300-305.

[2] Kumar P V, Scholts R A, Welch L R. Generalized bent function and their properties[J]. J Comb Theory A, 1985, 40(1): 90-107.

[3] Lidl R, Niederreiter H. Finite fields[M]. Cambridge : Cambridge University Press, 1994.

[4] Pott A, Tan Y, Feng T, et al. Association schemes arising from bent functions[J]. Des Codes Cryptography, 2011, 59(1-3): 319-331.

[5] Tan Y, Pott A, Feng T. Strongly regular graphs associat-ed with ternary bent functions[J]. J Combin Theory Ser A, 2010, 117(6): 668-682.

[6] Helleseth T, Kholosha A. Monomial and quadratic bent functions over the finite fields of odd characteristic[J]. IEEE Trans Inf Theory, 2006, 52(5): 2018-2032.