卷绕头的恒线速度卷绕
陈 斌,段隆江
(太平洋机电(集团)有限公司,上海 200090)
卷绕头作为化纤长丝纺丝的最后部件,其作用是将前道纺成的成形长丝卷绕成一定规格的圆柱形卷装。为了便于后续加工或应用,要求卷装成形的化纤长丝保持设定的纤度和适当的张力。但是,纺丝过程中,化纤长丝是以设定的固定线速度到达卷绕头,因此,要获得合格的圆柱形卷装,则拖动筒管形成卷装的锭轴的转速必然要随着卷装直径的增大而相应减慢,以实现恒线速度卷绕[1]。本文详细介绍一种实现恒线速度卷绕的方法。
1 提出问题
化纤长丝卷装的形式如图1(a),长丝卷绕在直径为D0的筒管上,形成直径为Dx(mm)高度为H的圆柱体。纺丝速度Vs(m/min)可分解为直线速度Vf(m/min)和横动速度Vr(m/min)两部分,如图1(b),其中α为卷绕角。
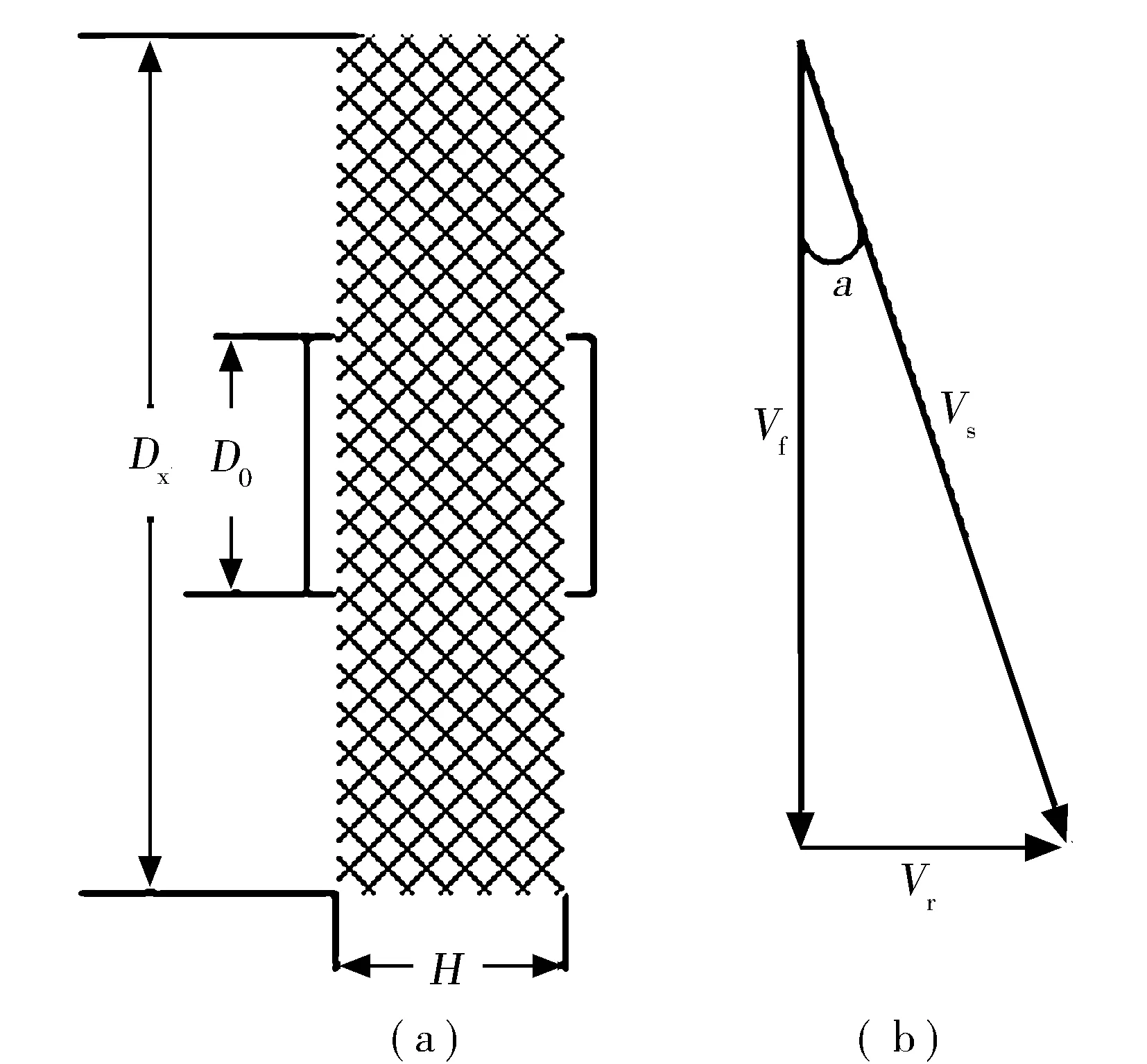
图1 卷装示意图
由卷装的成形方式可以得到:
(1)
其中:n—锭轴转速,r/min。
由式(1)可以看出,要保持纺丝速度Vs不变,则随着卷装直径Dx的增加,锭轴转速n必须相应降低。
卷绕头面世之初,锭轴是靠摩擦辊的摩擦传动来实现恒线速度卷绕,但随着纺丝速度的增加,摩擦传动严重影响纺丝质量,故目前锭轴均为直接驱动,通过直接控制电机的转速来实现恒线速度卷绕[2]。
据文献介绍有三种导出锭轴传动控制的方法,方法一是通过化纤长丝成品纤维线密度定义导出;方法二是通过某一卷绕时间内卷装质量导出;方法三是通过检测接触辊和锭轴实际转速的方式导出[3]。前两种方法自身存在局限性,第三种方法可以作为卷绕头设计的依据。但是,因为其推算的依据是已经纺成的卷装的直径,所以根据其给出的数学模型进行控制,锭轴的转速总是偏快,使得卷装中长丝的张力偏大。本文对第三种方法进行了改进。
把整个卷装看作密度均匀的圆柱体,它是一层一层的慢慢卷绕而成的。在锭轴传动的控制中,设定某控制周期,则每一个控制周期中形成的卷装的体积是相同的[4]。由卷装形成的这个关系可以根据前三个周期中卷装的直径来推算出下一周期结束时卷装的直径大小,从而可以根据这一预知的直径和设定的纺丝速度值由式(1)计算出下一周期中应该发出的锭轴的转速,达到真正的实时控制,解决了上述方法三中存在的问题,并且,只要选定的运算周期足够小,完全能够达到卷绕张力恒定的要求。
2 数学模型的推算
设定锭轴传动控制的周期为T秒,使得控制设备记录最近三个周期结束时卷装的直径值。在每一个控制周期中以T秒为采样周期通过安装在锭轴上的传感器实时地采集其转速,用以计算卷装的直径,此直径值为采样周期内形成的卷装的平均直径。
(2)
其中:Vf—设定的纺丝速度,m/min;
dx—平均直径,mm。
卷绕时已完成的最近三个和接下来将要完成的一个控制周期的示意图如图2所示。 设五个实线圆直径从小到大分别为Dn-3,Dn-2,Dn-1,Dn和Dn+1,前四个代表已经卷好的最外4层的外直径,第五个是需要推算的下一周期后形成的卷装的外直径。五个实线圆形成四个圆环,根据上述,这四个圆环的面积是相等的。设四个圆环的中心圆以直径从小到大分别为dn-2,dn-1,dn和dn+1,其中dn-2,dn-1和dn可根据采样的锭轴转速计算获得。这样,数学模型的推算问题即可描述为用dn-2,dn-1和dn表示出Dn+1。
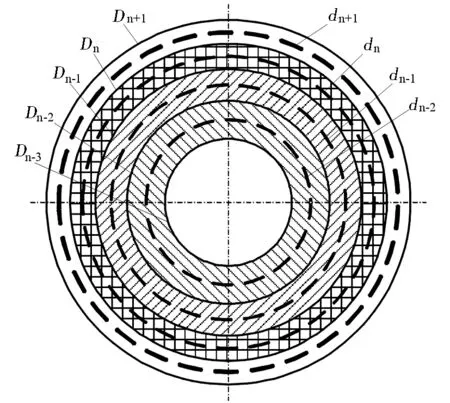
图2 卷装分层示意图
根据前述,可得到方程组:
(3)
方程组(3)中,有4个未知量Dn,Dn-1,Dn-2和Dn-3,正好有4个关系式,所以方程组有唯一解。
解得:
(4)
在得到Dn-3,Dn-2,Dn-1和Dn后,既可以得到Dn+1的精确值:
(5)
但因式(5)存在较复杂的数学运算,用作控制依据将对控制设备有很高的运算要求,故需要通过近似处理,得到Dn+1简化数学模型。
近似处理1:假设即将卷绕的一层的外直径的大小为目前卷装的外直径加上已经卷绕的最后一层的厚度的2倍,即:
Dn+1=Dn+(Dn-Dn-1)=2·Dn-Dn-1
(6)
将式(4)代入式(6)整理得式(7)如下:
Dn+1=dn-6·dn-1+3·dn-2+
(7)
近似处理2:设dn-dn-2=2dn-1-dn-2,则式(7)可以变换为:
Dn+1=4·dn-6·dn-1+3·dn-2
(8)
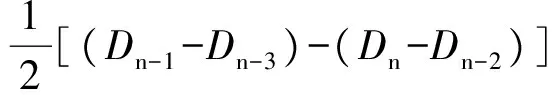
(9)
把式(9)作为递推公式,在excel中进行验算可知所推算的直径已经达到很高的精度。
理论验证数学模型的计算数值见表1。 最初三层的卷绕时,因控制设备未能采集到用作估算的三个数据,则以筒管的外径代替以完成估算。从理论验算的数据可以看出,式(9)估算出的直径值已经具有非常高的精度,除了最初的三层,其他完全能够满足1.5‰的卷绕控制精度要求,并且达到了控制精度100倍以上的精度,可以作为设备设计的数学模型。

表1 模型精度的理论验算
3 实际应用
XXX型卷绕头上,实际应用了上述恒线速度卷绕方法,效果良好。控制系统的组成示意见图3。

图3 控制系统组成示意图
控制器完成采集数据的分析与储存,并运用前述数学模型进行相关运算,然后把计算得到的锭轴转速所对应的频率发送给变频器,达到驱动锭轴的目的。
实际纺丝过程中,实时地采集锭轴转速和摩擦辊的转速,将所得数据化成曲线,见图4。

图4 锭轴和摩擦辊转速随直径增大的变化曲线
4 存在的问题及解决方法
观察采集的实际纺丝过程中的实时数据发现,估算的直径偶尔会出现跳跃。经分析,出现这种情况的原因为:受纺丝现场或其他干扰信号的影响,锭轴转速的采集可能出现偏差,从而使得相应的计算出现误差。估算的直径发生跳跃,将会使得以其为根据计算得到的锭轴转速发生突变,影响纺丝质量。
针对出现的问题,增加对计算得到的估算直径的校验程序。校验规则如下:
(1) 若测出的dn≤dn-1,则取dn=dn-1,若估算的Dn+1≤Dn,则取Dn+1=Dn;
(2) 若测出的dn≥(1+0.15%)dn-1,则取dn=1.015dn-1;若估算出的Dn+1≥(1+0.15%)Dn,则取Dn+1=1.015Dn
增加估算数据的校验程序后,估算直径跳跃的现象得到解决。
5 结 论
(1) 将长丝卷装的形成过程看作是分层逐步卷成的,通过实测已经卷成的卷装的直径,估算正在形成的一层的直径,从而设定锭轴的转速,达到恒线速度卷绕的目的;
(2) 详细介绍了实现结论1的卷绕方法所用的数学模型的推算过程,得到了理论精度非常高的、简化的数学模型;
(3) 对结论1和2进行实际应用,纺丝完全达到预定效果。
[1] 魏建.化纤高速纺丝机的锭轴传动控制技术[J].中国纺织大学学报,2004,26(2):65.
[2] 魏建,汤以范.恒线速卷绕的锭轴传动控制方法分析[J].合成纤维,2004(增刊):25.
[3] 魏建,汤以范.化纤高速卷绕机锭轴传动控制方法的分析[J].东华大学学报(自然科学版),2003,29(5):59-62.
[4] 熊光洁、蔡玉华.化纤卷绕过程的机电一体化研究[J].北京工商大学学报(自然科学版),2004,22(4):26-27.

