如何将数学美融入高职数学课教学中

王玲芝

（天津现代职业技术学院，天津市 300222）

有现象表明，教育界和学术界的某些思维方式正在深陷纯粹实用主义的泥潭，其表现是急功近利、心浮气躁，、这种病态心理正在病入膏肓，且波及到接受教育的各个层面，高职教育也不例外。其后果造成了每一个学生经历十几年的数学课的学习，很多人并未掌握数学的精髓。相反，在高职层面大多数学生对数学思想了解的比较肤浅，数学素质较差；甚至对数学产生恐惧心里，误以为学数学就是为了会做题、应付考试，不知道“数学方式的理性思维”“数学中还有美”的重要文化品格价值。其实，对于这种文化品格的数学训练，能陶冶一个人的情操，提升一个人的综合素质水平，都有非凡的功效。实际上当他们走人社会，从数学课程学习中获得的数学素养，数学的思维方法和看问题的着眼点随时随地都会起作用，终身都会受益。而数学美正是以一种平和的心态在寻求这种“寓教于乐”中实现提高学生的数学素养。本人在教学中努力地做过这样的尝试把数学的自身成分与数学的精神，思想，方法的数学美融入教学中，其目的就是教会学生在美的享受中使其心灵得到亲切感，产生求知热情，培养对数学的良好情感和激励对数学的探索、求真、创新的精神。并旨意作为推广数学文化及数学美理念的传播者。

一．数学美在融入高职数学教学课堂中的定位

什么是数学美？它的本质是什么呢？从国内的研究来看，有这样一些描述：“数学美是一种人的本质力量通过宜人的数学思维结构的呈现”，“数学美是数学创造的自由形式”，“数学美是真与善的统一”，“数学美的本质在于序”……等等。

数学美的主要特征：

1．数学美的客观性

即指客观存在于数学领域中的审美对象是不以审美主体是否承认、是否意识到为转移的，尽管因审美主体的主观条件的不同，并不是所有的或特定的数学美都能为审美主体所感知，但这并不能改变数学美的存在。

2．数学美的物质性

数学美的内容——人的本质力量必须通过某种形式呈现出来，必需要有附体，数学美的这种形式或附体，即数学美的物质属性。

3．数学美的宜人性

即数学美形式应该使审美主体感到愉悦。审美主体的愉悦性，一方面自然是由审美主体的心理和生理的原因造成的，另一方面，也是最根本的，还在于对象本身是具有足以引起主体愉悦的属性和条件。简言之，数学美的形式必须与人的认识、人类心灵深处的渴望的本质上相吻合。

数学美在融入高职数学教学时应充分体现它的主要特征。

首先，数学美不应、也不可能成为直接的追求目标或教学对象。对数学美的鉴赏需要对于相应数学理论的熟悉，即数学美应以相应的知识为载体—数学美的物质性，不承认它的物质性，也不能全面理解数学美的本质，如果离开这些物质因素，数学美的内容——人的本质力量则无从体现。因此，我们所涉及的数学美的内容，应锁定在高等职业教育所应掌握的数学理论上（涉及微积分、线性代数、概率论与数理统计等课程）。

其次，一个特别重要的问题在于数学美具有一定的客观性是肯定的。但这种客观性又是否可以完全被归结为所涉及的数学对象的特殊属性，从而就在很大程度上不带有任何主观成分，答案又应该是否定的。数学家对数学美的判断虽然是高度一致，但是这种数学美不能完全被归结为相应的数学对象所具有的特殊属性，也就是不能忽视数学家的主动地位。数学是冷而严肃的，客观上来说，根据美感在人们头脑中显现的难易程度，数学是比艺术美、自然美最难感受的美，再加之高职院校的学生一般都有基础薄弱、学习兴趣不浓、思维能力特别是抽象思维能力不高的问题，这都会使我们在融入过程中带来很多困难。这是一方面，但另一方面，数学中有艺术，有美，数学的创造过程中有数学家及数学爱好者的情感。冷漠、严肃主要是相对于数学的真理性而言的，但是数学真理之中也凝结着数学家的情感。因此，教学中，这就需要教师在将数学美融入教学时针对高职学生的基础状况，尽量做到直观化、通俗化，逐步抽象化，让学生易于接受。教材内容的引入尽可能地从学生熟悉的生活实例或与专业相结合的实例所能体现出的美因中引出，拓宽学生的视野，这有利于提高学生把实际问题转化为数学问题的能力。同时，我们也要展示思维过程，就是要学生看到数学家活生生的思考问题的方法，更深刻地理解数学内容；我们要求重视数学思想方法的教学，就是要学生不仅掌握具体的数学知识，而且也能领会内在的精神实质，掌握打开知识宝库的钥匙，欣赏到数学的理性美。总之，应体现出教师的主观能动性极大限度地将数学美都能为审美主体所感知。

最后，我们还要强调的是教师如何搭建符合高职学生的认知结构展示数学美内容的平台，将所展示数学美的形式唤起学生心灵深处的渴望达到的一种真正意义上的吻合。否则，就会造成自我陶醉，孤芳自赏。

二．数学美的主要表现形式的案例

1．体现对称美，增强数学魅力

对称性是指组成某一事物或对象的两个部分的对等性。数学形式和结构的对称性是对称美的自然表现。对称性是最能给人以美感的一种形式。德国数学家魏尔说：“美和对称性紧密相关。”数学中有着各种各样的对称。从几何图形看，有中心对称形、轴对称形、面对称形和转动对称形等。毕达哥拉斯说：“一切立体图形中，最美的是球形，一切平面图形中最美的是圆形。”因为这两种形体在各个方向上都是对称的。此外，象正多边形、正多面体、旋转体和圆锥曲线以及圆锥曲面等都给人以完善、对称的美感。就代数形式论，有对称多项式、对称方程式、对称恒等式、对称不等式和对称矩阵等。这些对称形式都是凭借理性可以感受到的令人愉悦的形式，当然其中也不乏具有感性美所特有的生动可感的具体感性形式。例如，行列式就被人们称为“美丽的花园”，它的每一边都可以扩展。一个三阶行列式是由九个元素按三行三列所排列成的正方形，即使不懂数学的人也能感受到其排列整齐和处处对称，领略到它的形式之美。在代数中轮换对称式表明了代数式中字母可以互换的对称关系。在数学解题方面，在数学教学中，不断地揭示对称美的因素，能使学生常受到美的熏陶，自觉地运用“对称”这一数学美的形式特征去解决具体问题，例如，在介绍完偏导数时，对于对称的二元函数z＝f（x，y）求偏导数，我让学生们从习题中把对称的二元函数都找出来，告诉他们此时只需求出对x偏导数z′x＝f′x（x，y），然后利用代数中轮换对称即可得到z′y＝f′x（y，x）。同学们会感到第一，可以减少一半的计算量。第一，可以体会到对x偏导数z′x＝f′x（x，y）一定不能出错。因此，他会不失时机地首先去寻找是否为对称的二元函数且会很仔细求出对x的偏导数。否则，就会适得其反。由此可利用到对称的二元函数z＝f（x，y）在附加条件也对称的二元函数φ（x，y）＝0下求极值问题。

先作拉格朗日函数L（x，y）＝f（x，y）＋λφ（x，y）

λ为参数，求对x偏导数z′x＝f′x（x，y）后，即可得到对y偏导数z′y＝f′x（y，x），使之为零，然后

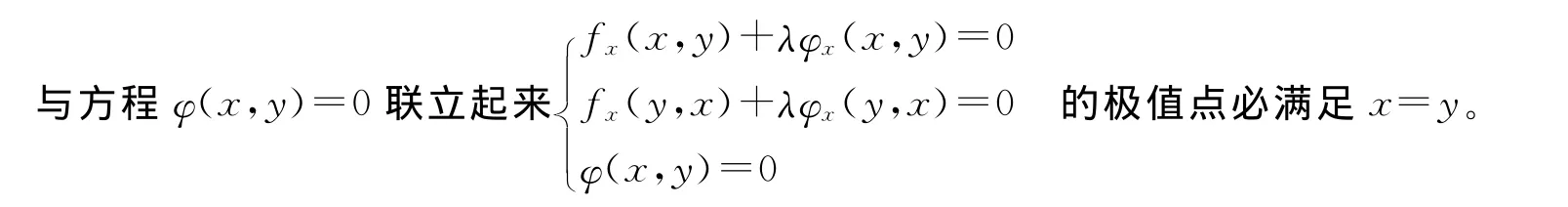
接着我又举了一个具体例子：求表面积为a2而体积为最大的长方体的边长。

设长方体的三棱长x，y，z为则问题就是在条件φ（x，y，z）＝2xy＋2yz＋2xz－a2＝0

下求函数V＝xyz （x＞0，y＞0，z＞0）的最大值。

作拉格朗日函数L（x，y，z）＝x yz＋λ（2xy＋2yz＋2xz－a2）这是一个对称的三元函数即直接可得x＝y＝z然后代入φ（x，y，z）＝2xy＋2yz＋2xz－a2＝0中，便得

对称方法往往使问题解决的过程简捷明快，同学们从中感到原本很复杂的联立方程的求解直接得到了结果。并进一步理解数学美的真正含义。

2．揭示统一美，知识融会贯通

统一性是指部分与部分，部分与整体之间的内在联系或共同规律所呈现出来的和谐、协调、一致。

数学美中的统一性在数学中有很多体现。数学推理的严谨性和矛盾性体现了和谐；表现在一定意义上的不变性，反映了不同对象的协调一致。例如，数的概念的一次次扩张和数系的统一，运算法则的不变性。

例如引人导数概念后，函数y＝f（x）的导数也叫微商记作y′或，两种表示形式差别较大，引人微分概念后，微分dx＝f′（x）dx

（15）一对平行平面x2－a2＝0 （16）一对虚平行平面x2＋a2＝0

（17）一对重合平面x2＝0

和展示完优美的图形后，让学生们把日常生活中见到过哪些曲面找出来，有的同学开玩笑地说，圆筒冰激凌是下面是锥面上面扣着个球面，课堂气氛很活跃，但考虑到这些方程要记住又犯难了，此时，我把它们放在更开阔的视野下，统一在一个带有三个变量的二次方程包含10项的一般形式，如下：

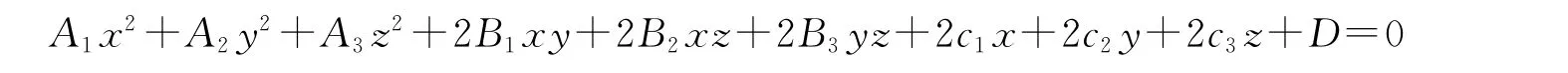
对于上述这个一般形式，告诉他们经过适当的变换或这些常数的取值便可到二次曲面的各个标准方程。

需要说明的是，最后9个标准方程（9）～（17）不包含z的项正是平面oxy上二次曲线的标准方程。在空间中这些方程都表示柱面。这里我们看到的是平面二次曲线和空间二次曲面的高度一致，体现出一种统一美。

在方程（1）～（8）中，方程（2）不被任何有实数坐标（x，y，z）的点所满足，而（6）只有坐标原点的点满足它。而这里的“虚”曲面并不存在。虚曲面是人们的一种理论模式，因为它合于完备性的一种要求，呈现一种对称美。这些标准方程统一在一个三个变量的二次方程中，我们又一次看到数学和谐中的统一美，一致美。

基于数学理论的美既不是客观事物与客观规律本身，也非人的思维和思维本身，而是人的数学思维的美和自然界客观规律美的对立统一，人的思维对自然界规律美的反映是一个无止境的过程，而人的数学思维对自然界规律的反映所形成的数学理论美也是一个无止境的过程，又由于客观规律存在着的美处于运动的永恒过程之中，因此数学思维的美和自然界客观规律美可能会有偏差。所以我们所谈到的数学美，其中有与数学审美标准中比较一致的数学美，也有本人依据数学美学理论对数学美的独特看法。但未来数学思维的美和自然界客观规律美应趋于一致，二者就像双曲函数和它的渐近线一样几乎同步地向前延伸，彼此不断接近，然而永远不会重合。

心理学研究表明：没有丝毫兴趣的强制性学习，将会扼杀学生探求真理的欲望。兴趣是思维的动因之一，兴趣是强烈而又持久的学习动机。只有学生热爱数学，才能产生积极而又持久的求学劲头。因此，如何充分运用数学美的诱发力来引起学生浓厚的学习兴趣、强烈的求知欲望，对学生学好数学这门课有着重要和积极的作用。

［1］吴振奎．数学中的美［M］．上海：上海教育出版社，2004．

［2］易南轩．数学美拾取［M］．北京：科学出版社，2002．

［3］张顺燕．数学的美与理［M］．北京：北京大学出版社，2004．

［4］叶宝生．科学之美［M］．北京：中国青年出版社，2002．

［5］方延明．数学文化 ［M］．北京清华大学出版社，2009．

［6］郑毓信．数学思维与数学方法论［M］．成都：四川教育出版社，2005．

［7］顾沛．数学文化［M］．北京：高等教育出版社，2008．

［8］邹庭荣．数学文化欣赏［M］．武汉：武汉大学出版社，2007．