空间网壳结构极限承载力分析

李俊生

(铁道第三勘察设计院集团有限公司,天津 300251)

在大中型铁路车站和大型体育场馆中,为了实现较好的空间造型和较大的跨度,空间网格结构尤其是空间网壳结构得到了极为广泛的应用。空间网壳结构以其经济、高效、美观的特点深受建筑师和结构师的青睐。空间网壳结构大多数为多次超静定的空间杆系结构体系,也就是说,当结构承受荷载时,部分杆件的受拉屈服或受压失稳并不能引起网壳结构的整体破坏,只有当屈服或失稳的的杆件足以使结构成为机构时,网壳结构才达到极限承载力。相较于空间网架,网壳结构受压杆件更多,杆件屈曲对其影响更大[1]。

1 研究实例简介及建模

老山自行车馆屋盖双层球面网壳如图1所示,以四角锥网格为主,径向网格32个,最外圈环向网格96个,向内经多次收格使网格大小均匀,网壳杆件采用圆钢管截面,钢管规格为φ114×4～φ203×12,节点为焊接空心球节点,规格为φ300×12～φ600×24(加肋),屋盖结构示意如图2所示。球面网壳周边通过环形桁架支承于人字形钢柱柱顶,环形桁架由4根环梁通过腹杆连接而成,如图3所示,全部采用圆钢管截面,其中网壳上、下弦周边的3根环梁截面为φ500×16,人字形钢柱柱顶环梁截面为φ1 200×20,环梁与腹杆及与人字形钢柱均采用钢管相贯节点相连。人字形钢柱沿环向倾斜设置,共24对,截面为φ1200×18的圆钢管,柱脚采用铸钢球铰支座节点。除柱脚铸钢节点钢材为GS-20Mn5N外,全部钢结构采用Q345钢材制作,其中室内钢结构钢材为Q345B,室外钢结构则采用Q345C,以确保低温下的材料性能。

图1 老山自行车馆整体效果图

图2 北京2008奥运会老山自行车馆屋盖结构示意(单位：mm)

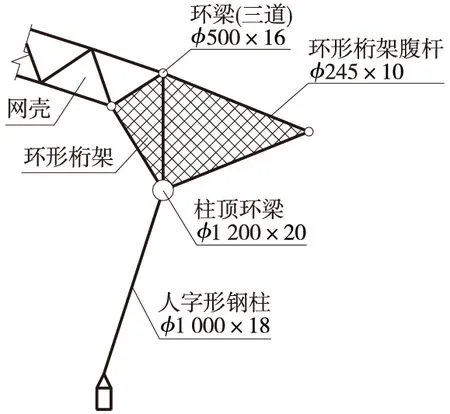
图3 环形桁架示意(单位：mm)

结构荷载取值如下。

(1)结构自重：设计软件按构件轴线长度自动计算结构自重,并放大1.2倍以考虑节点自重；

(2)屋面恒荷：屋盖中部直径D=59.128 m范围内为采光玻璃屋面0.90 kN/m2,周边采用金属板屋面0.40 kN/m2；

(3)吊挂荷载：金属板屋面区域下平均吊挂荷载0.50 kN/m2,包括马道、风道、音响及灯具等；

(4)屋面活荷：0.50 kN/m2；

(5)风荷载：风荷载按《建筑结构荷载规范》(GB50009—2001)并参考风洞试验结果确定,基本风压0.45 kN/m2,风压高度变化系数按网壳最高点高度35.5 m、B类地面粗糙度取为1.49,体型系数按旋转壳体(矢跨比≤1/4)偏于安全地取为-1.0(风吸力),风振系数根据风洞试验结果取为2.5,风荷载标准值：wk=2.5×1.0×1.49×0.45=1.68 kN/m2；

(6)雪荷载：基本雪压0.40 kN/m2,积雪分布系数偏于安全地取1.0,雪荷载标准值sk=0.4 kN/m2,雪荷载不与屋面活荷载同时考虑；

(7)温度荷载：根据北京全年气温变化情况,取网壳设计合龙温度+10 ℃,设计温差±30 ℃,设计覆盖的温度范围为-20～+40 ℃；

(8)地震荷载：结构抗震设防烈度为8度,基本地震加速度0.20g,场地土类别II类,设计中考虑水平及竖向地震作用。

在本文进行极限承载力分析时,只考虑竖向恒载和竖向活载作用,不考虑风荷载等其他荷载,采用荷载组合为：1.35恒荷载+0.7×1.4活荷载(恒载起控制作用)。

本文采用ANSYS有限元软件对2008北京奥运会老山自行车馆建立模型和进行分析。根据已有设计资料中的节点坐标、杆件节点信息以及荷载信息编辑命令流,再由ANSYS运行命令流,进行结构分析。为了得到更好的结果,要先打开弧长法再进行分析,在弧长法的设置中值得注意的一项是，要选大变形小应变假定,因为本文在对空间网壳结构进行分析时是允许大变形的,而钢材则是小应变的材料。通过不断改变最大弧长和最小弧长来筛选最好结果。为了求得空间网壳结构的极限承载力,本文中网壳结构的加载范围为0～3倍的设计荷载,荷载从0开始,逐级加载,直至极限荷载。

当对一个结构进行逐级加载时,结构杆件的内力以及结构的位移也会不断增加,当杆件没有屈曲时,结构的荷载-位移曲线是线性的。可是随着荷载的增加,结构的部分杆件开始屈曲,此时结构的荷载-位移曲线将呈现非线性变化。当荷载加至结构的极限荷载时,结构就会发生卸载现象,也就是说荷载不再随着位移的增加而增加,反而随着位移的增加而下降,这样在结构的荷载-位移曲线上就会出现一个峰值点,得到这个峰值点,也就得到了结构的极限荷载。在本文的分析中,打开弧长法的一个作用就是能得到结构达到极限荷载后荷载-位移曲线及荷载-位移曲线的下降段部分[2]。

2 不考虑节点刚度和压杆失稳问题分析

在ANSYS软件中建模时,采用LINK8单元,假定空间网壳结构所有节点为铰接,但不考虑压杆失稳问题,所用模型的应力-应变关系如图4所示,开始时杆件的应力和应变为线性关系,当杆件达到屈曲点σs(σs=345 MPa)时,其应力不再增加,而应变则继续增加。

图4 不考虑压杆失稳的杆件受力模型

经过分析,得出在不考虑压杆失稳和节点刚度情况下,结构屋顶顶点(结构中位移最大点)的荷载-位移曲线如图5所示。

图5 不考虑压杆失稳和节点刚度的荷载-位移曲线

图5的横坐标轴为空间网壳结构屋顶顶点(结构中位移最大点)的位移,纵坐标为结构的荷载因子,其值乘以3以后得到的就是结构设计荷载的倍数。由图5峰值再结合ANSYS分析所得数据，得出在不考虑压杆失稳和节点刚度时空间网壳结构的极限承载力为设计荷载的2.925(3×0.975)倍,此时结构位移为0.913 m。

3 不考虑节点刚度和考虑压杆失稳问题分析

图6 考虑压杆失稳的杆件受力模型

考虑压杆失稳问题时,同样采用LINK8单元,假定空间网壳结构所有节点为铰接,所用模型的应力-应变关系如图6所示,拉杆的应力-应变关系与不考虑压杆失稳问题时是一样的,但压杆的应力则只增加到受压杆件的受压临界力σcr(σcr=π2Et/λ2)时就不再增加了。可以预见,考虑压杆失稳问题时计算得出的空间网壳结构极限承载力要比不考虑压杆失稳问题计算得出的极限承载力低一些。

在考虑压杆失稳但不考虑节点刚度时,分析得出的空间网壳结构屋顶顶点荷载-位移曲线如图7所示。结合图7和ANSYS分析结果得出,在考虑压杆失稳但不考虑节点刚度时空间网壳结构的极限承载力为设计荷载的2.742(3×0.914)倍,而其相应的位移为0.618 m。从这两项数据可以看出,与不考虑压杆失稳问题时相比,无论是极限承载力还是达到极限承载力时空间网壳结构屋顶顶点的位移都降低了。这说明由于部分长细比较大的压杆的受压临界应力小于其屈曲服点,导致了这些杆件过早的屈曲或者不考虑压杆失稳问题时没有屈曲但在考虑压杆失稳问题时屈曲了,从而使得极限承载力下降。

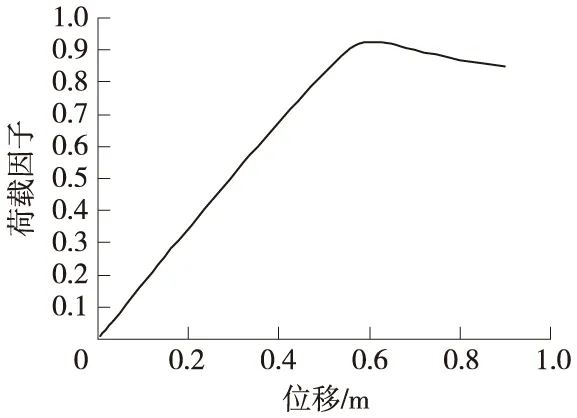
图7 考虑节点刚度但不考虑压杆失稳时荷载-位移曲线

比较两次分析结果,不难看出,在考虑压杆失稳的情况下,结构的屈曲杆件明显增多了,极限承载力和相应位移有所下降,极限承载力下降了0.183倍的设计荷载。由于部分长细比较大的杆件的受压临界应力要小于其屈服点,所以一些在不考虑压杆失稳问题时未屈曲的杆件在考虑压杆失稳问题时屈曲了,但由于前者的极限荷载低于后者,也使一些在不考虑压杆失稳问题时屈曲的杆件在考虑压杆失稳问题时没有达到其极限荷载而不屈曲失稳。还有值得注意的就是,在考虑压杆失稳问题进行分析时,部分受压腹杆出现了屈曲。虽然考虑压杆失稳问题时空间网壳结构的极限承载力有所降低,但降低是比较小的,这是由于受压临界应力较小的杆件在整个结构中所受的力也比较小,因而考虑压杆失稳问题并没有使该空间网壳结构的极限承载力下降很多,这也充分说明了2008北京奥运会老山自行车馆空间网壳结构设计的合理性。

4 考虑节点刚度但不考虑压杆失稳问题分析

本文在考虑节点刚度但不考虑压杆失稳问题对空间网壳结构进行分析时,假定空间网壳结构的单元由杆单元变为梁单元,单元两端节点刚结,在ANSYS分析中采用BEAM188单元。经分析得出空间网壳结构屋顶中点的荷载-位移曲线如图7所示。

观察图7并结合ANSYS分析结果,可以得出,当加载到2.508(3×0.836)倍的设计荷载时,曲线开始呈现非线性变化,说明开始有杆件屈曲,这个值要比不考虑节点刚度和压杆失稳问题时大一些,说明由于节点刚结使得杆件屈曲较晚。当加载到设计荷载的2.778(3×0.926)倍时,曲线达到峰值,说明空间网壳结构达到了极限荷载,相应的空间网壳结构屋顶中点的位移为0.597 m。这个值与不考虑节点刚度的分析结果相比,稍小了一点,但相差不多。这说明在本文的分析中,节点刚度对极限承载力基本没有影响。

5 综合比较

本文是分析空间网壳结构的极限承载力并讨论压杆失稳和节点刚度对空间网壳结构极限承载力的影响,所以很有必要将3种情况下的空间网壳结构屋盖顶点的荷载-位移曲线放到一张曲线图里来比较,以便进行综合分析,从而得出压杆失稳和节点刚度对极限承载力的具体影响。图8即为3种情况下的荷载-位移曲线。

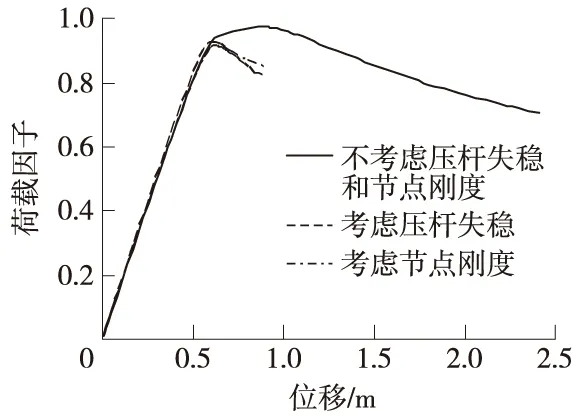
图8 不同情况下的荷载-位移曲线``

观察图8,再结合ANSYS分析结果,可以得出极限承载力由大到小依次为：不考虑压杆失稳和节点刚度时、考虑节点刚度但不考虑压杆失稳问题时、考虑压杆失稳但不考虑节点刚度；达到极限承载力时相应的空间网壳结构屋顶顶点位移由大到小依次为：不考虑压杆失稳和节点刚度时、考虑压杆失稳但不考虑节点刚度时、考虑节点刚度但不考虑压杆失稳问题时；达到极限荷载时空间网壳结构屈曲的杆件数由多到少依次为：考虑压杆失稳但不考虑节点刚度、不考虑压杆失稳和节点刚度时、考虑节点刚度但不考虑压杆失稳问题时。以上比较说明,考虑压杆失稳时结构的极限承载力略有下降,节点刚结并没有提高结构的极限承载力,只是一定程度上限制了结构的位移。

继续观察图8可以发现：在线性阶段,曲线“不考虑压杆失稳”和曲线“考虑压杆失稳”是重合在一起的,这说明在未出现杆件屈曲及压杆尚未达到其受压临界力时,考虑压杆失稳与否是不影响结构的杆件内力的。

6 结论

本文的任务是要分析2008北京奥运会老山自行车馆空间网壳结构的极限承载力,并分析压杆失稳问题和节点刚度对空间网壳结构极限承载力的影响,可以得出如下结论。

(1)2008北京奥运会老山自行车馆空间网壳结构的极限荷载为设计荷载的2.7倍以上,这说明该空间网壳结构的设计偏于安全,同时也说明空间网壳结构这种结构形式安全可靠性较高,是适应现代建筑要求的一种优良结构。

(2)由于长细比较大的压杆的受压临界应力小于其屈服点,致使空间网壳结构极限承载力在考虑压杆失稳问题时有所降低。但由于本文所讨论空间网壳结构受压临界力较小的杆件在整个结构中受力也较小,致使考虑压杆失稳问题对极限承载力的影响不大,所以极限承载力降低的并不是很多。

(3)节点刚结并没有提高本文所研究空间网壳结构的极限承载力,只是在一定程度上限制了整个结构的位移。

[1]蓝 天.空间钢结构的应用与发展[J].建筑结构学报,2001,22(4)：2-8．

[2]陈 昕,沈世钊.网壳结构的几何非线性分析[J].土木工程学报,1990,23(3)：47-57.

[3]吕晓亮.青岛客站风雨棚网壳结构设计[J].铁道标准设计，2009(11)：118-120.