铁路选线设计方案物元优选模型及其应用研究

陈 俊,邵海鹏

(1.中铁第四勘察设计院集团有限公司,武汉 430063；2.长安大学公路学院,西安 710064)

铁路选线设计是一个集决策和设计为一体的、多因素、多层次的复杂工程系统,涉及因素众多,既有运营条件、工程条件、工程费、运营费等定量指标,又有施工及环境影响、社会政治经济意义等定性指标。传统的评选方法是在经济上追求换算工程运营费最省,并结合对各方案的技术条件、环境影响和社会作用等因素的分析,得出最佳方案。由于传统方法在方案较多,且各方案的定性指标特征值出现交叉,各有所长,经济上又差别不大的情况下,很难确定出一个较优方案,而且不能将技术经济定量指标和社会环境影响定性指标综合起来。本文中通过对铁路选线设计方案评价指标的分析研究,应用物元可拓学[1]理论,提出了铁路选线设计方案优选综合评价模型。

1 优选等级划分标准

铁路选线设计方案优选是一个反复迭代、不断改善、逐步逼近最佳方案的过程。根据铁路选线设计方案的状况及其评价等级的特征,将优选等级划分为4个等级：优、良、及格、差[2],如表1所示。

表1 铁路选线设计方案优选等级划分标准

2 铁路选线设计方案评价指标体系

铁路选线设计方案评价指标体系的构建是定性分析和定量研究[3]相互结合的过程。定性分析主要考虑评价指标的完备性、针对性、稳定性、独立性等因素,主观确定指标及其结构的过程,定量研究则是通过一系列检验,使评价指标体系更加科学和合理的过程。根据构建铁路选线设计方案评价指标体系的方法和原则,从技术可行性、经济合理性、施工及环境影响以及社会政治经济意义4方面,先进行评价指标初选,在此基础上,剔除一些与铁路选线设计相关性不大的指标,提出了一个由目标层、准则层、指标层构成的递归层次体系[4～5],如图1所示。

图1铁路选线设计方案评价指标体系

该评价指标体系在空间上反映出铁路选线设计方案的空间布局和结构,在层次上反映其功能和水平,主要从宏观和微观2个层面来体现铁路选线设计方案的内涵。

3 铁路选线设计方案的物元评价模型

3.1 可拓学及物元模型

在客观世界中,事物是质与量的统一体,因此事物的变化有量变和质变之分。在解决矛盾问题的过程中,既要考虑量的变化,又要考虑质的变化。可拓学把质与量有机结合起来,引入了物元概念,从定性和定量两方面去研究解决矛盾问题的规律和方法,通过建立多指标评价模型,完整地反映待评对象的综合质量水平。可拓学的定量化工具是可拓集合理论,包括可拓集合、关联函数、可拓关系等[2]。

可拓学的理论支柱是物元理论和可拓集合论,其逻辑细胞则是物元概念,是以事物、特征及事物关于该特征的量值所组成的三元组,记作R=(事物,特征,量值)。可拓集合既不同于经典集合所描述的确定性概念,也不同于模糊集合所描述的模糊性概念。物元的概念正确地反映了质与量之间的关系,可以贴切地描述客观事物变化的过程,为解决评价问题提供了一个新的途径。

其基本步骤如下。

(1)确定经典域R0j

式中，N0j表示所划分的j个等级；ci为等级N0j的特征,表示第i个评价指标；x0ji为N0j关于ci所规定的量值范围,即各类别关于对应的评价指标所取的数据范围经典域。

(2)确定节域Rp

式中，p为等级的全体；xpi为p关于ci所取的量值范围,xpi=〈api,bpi〉(i=1,2,…,n)。

(3)确定待评物元

对于待评对象,把得到的数据或分析的结果用物元表示

式中，p0为待评对象；xi为p0关于ci所取的量值,即待评对象的具体数据。

3.2 铁路选线设计方案的物元评价

本文将可拓学理论及物元模型应用在铁路选线设计方案优选的综合评价中。在前面建立评价指标体系的基础上,利用物元分析方法建立多指标评价模型,根据关联函数求出待评对象对于某一信用等级的关联度,从而较为全面地反映待评对象的信用程度[1]。

(1)确定各项指标的权系数

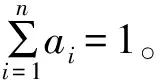
第二层的判断矩阵B1、B2、B3、B4具体如下

B1=

针对构造的5个判断矩阵,用方根法对其特征向量做归一化和正规化处理[5],计算各层次的权重集,具体如下：

A0=(0.482 9,0.272 0,0.157 0,0.088 1),λ0max=4.014 5,CR0=0.005 422 9<0.1

B1=(0.251 6,0.167 0,0.148 5,0.118 7,0.095 2,0.084 2,0.055 8,0.047 0,0.032 0),λ1max=4.125 7,CR1=0.028 227<0.1

B2=(0.417 5,0.166 5,0.180 5,0.093 6,0.085 2,0.056 7),λ2max=6.090 1,CR2=0.014 425<0.1

B3=(0.400 3,0.206 5,0.219 3,0.109 7,0.064 2),λ3max=5.025 8,CR3=0.005 760 5<0.1

B4=(0.380 1,0.221 1,0.173 8,0.118 2,0.054 9,0.051 9),λ4max=6.183 7,CR4=0.029 406<0.1

判断矩阵的随机一致性比率CR=CI/RI<0.1,验证了判断矩阵具有满意的一致性,说明权数分配是合理的[7]。并将单层次权重值转换成合成权重值,得出26个评价指标的权重系数,即A=(a1,a2,…,a11)=(0.121 5,0.080 6,0.071 7,0.057 3,0.046 0,0.040 7,0.026 9,0.022 7,0.015 5,0.113 6,0.045 3,0.049 1,0.025 5,0.023 2,0.015 4,0.062 8,0.032 4,0.034 4,0.017 2,0.010 1,0.033 5,0.019 5,0.015 3,0.010 4,0.004 8,0.004 6)。

(2)确定待评铁路选线设计方案优选等级的关联度

Kj(xi)=

式中

x0ji=〈a0ji,b0ji〉,xpji=〈apji,bpji〉

(3)计算铁路选线设计方案优选等级的关联度

Kj(p0)为待评对象p0关于等级j的关联度。

(4)铁路选线设计方案优选评定

若Kj0(p0)=maxKj(p0),其中j∈(1,2,…,n),则待评铁路选线设计方案p0等级为j0级[2],若对一切j,Kj(p0)≤0,表示铁路选线设计方案优选等级已不在划分之内。

4 实证研究

以某铁路为例来充分说明铁路选线设计方案优选评价,设计方案优选评价各等级经典域为

当j=1,2,3,4时,N0j分别为{优}、{良}、{及格}、{差},x0ji量值范围分别对应<70,100>,<40,69>,<10,39>,<0,9>。

节域为

Rp=(p,ci,xp)=

针对某铁路选线设计方案优选所建立的26个指标,由专家测得各项指标的平均值。

即c1=75,c2=70,c3=65,c4=82,c5=76,c6=62,c7=55,c8=70,c9=63,c10=70,c11=73,c12=70,c13=62,c14=65,c15=70,c16=68,c17=66,c18=73,c19=62,c20=69,c21=72,c22=65,c23=75,c24=74,c25=71,c26=68。表示成待评物元为

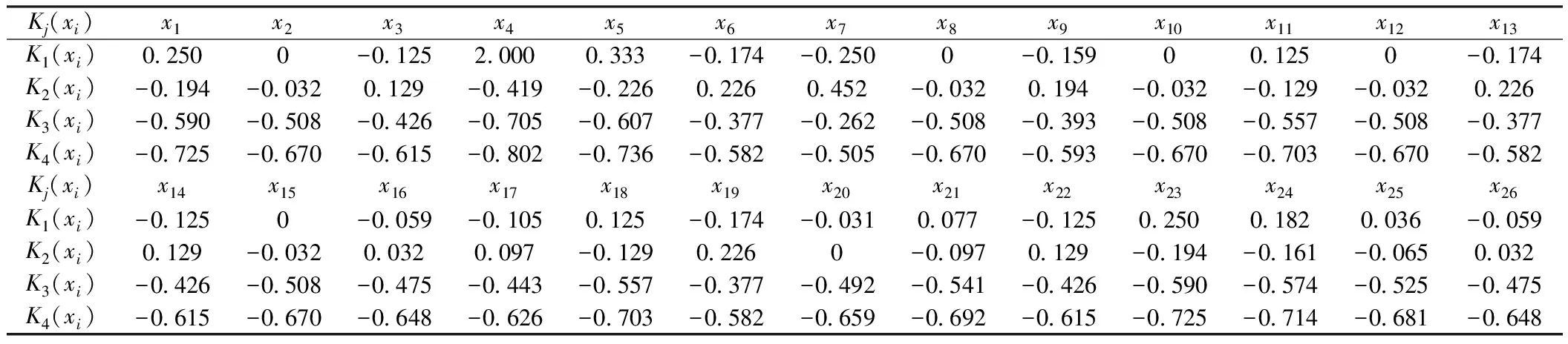
表2 某铁路选线设计方案优选评价等级的关联度Kj(xi)具体数值

5 结语

根据铁路选线设计方案优选评价内容和特点、技术可行性、经济合理性、施工及环境影响以及社会政治经济意义,建立了评价指标体系,并应用物元可拓理论,结合AHP权重确定方法,依据优选等级划分标准,提出了基于物元可拓理论的铁路选线设计方案优选综合评价模型,拓宽了物元可拓理论的应用范围,为铁路选线设计方案优选评价提供了一种新手段。此方法可以达到的目的为：(1)通过优选评价等级划分标准的确定,可以判定铁路选线设计方案优选达到的程度；(2)可以进行不同时期铁路选线设计方案的比较。

[1]蔡 文.物元模型及其应用[M].北京：科学技术文献出版社,1994:267-275.

[2]石为人,黄印林,唐松松.城市机动车交通资源状况的物元评判模型研究[J]. Proceedings of the 24th Chinese Control Conference, 2005,1634-1635.

[3]Zhou Wei, Zhang Shengrui, Sun Xiaoduan. Study on comprehensive evaluation of highway network by artificial neural network[A]. Proceedings of the 4thMeeting of Hong Kong Society for Transportation Studies[C]. Hong Kong∶Hong Kong Society for Transportation Studies, 1999:199-207.

[4]李远富,薛 波,邓域才.铁路选线设计方案多目标决策模糊优选模型及其应用研究[J].西南交通大学学报,2000,35(5)：465-470.

[5]易思蓉,张家玲.基于智能CAD系统的铁路选线方案多目标综合评价方法[J].铁道学报,2000,22(S1):95-101.

[6]常建娥,蒋太立.层次分析法确定权重的研究[J].武汉理工大学学报,2007,29(1)：153-155.

[7]CAI WEN. Extension Management and Application[J]. International Journal of Operations and Quantitative Management,1999,5(1)：59-72.