网络计划图中关键线路的求解方法探讨——以“生产与运营管理”课程的一道习题为例

朱良华

（梧州学院，广西 梧州 543002）

网络计划图中关键线路的求解方法探讨
——以“生产与运营管理”课程的一道习题为例

朱良华

（梧州学院，广西 梧州 543002）

关键线路主要应用于项目进度、网络优化、项目索赔等，是项目网络的瓶颈，准确求解网络图中的关键线路具有十分重要的意义。“生产与运营管理”课程中以一道习题为例，系统介绍了三种常用的求解关键线路的方法：时差法、线路时间比较法、破圈法。通过对比分析和思考，发现时差法并不适用于所有节点时差均为零的这一特殊网络图。由此得出，节点时差为零只是关键线路的必要条件，而非充分条件。在求解关键线路的时候，线路时间比较法和破圈法相对而言更加准确可靠。

网络计划图；关键线路；时差法

有研究表明，在组织管理中引入网络计划技术可比传统管理方法在工期上缩短20%左右，节约成本10%以上[1]。网络计划方法自上个世纪50年代中后期从美国逐渐发展起来后，目前正以其无可比拟的优越性受到工程界的普遍推崇，成为了项目计划管理的重要方法。在“生产与运营管理”课程中，关于网络计划方法的研究、尤其是关于关键线路的判断与优化是课程中的一个重要内容，也是学生学习起来觉得比较吃力的一个内容。在本文中，笔者主要根据个人对课程中的一道练习题的理解与思考，尝试对箭线型网络图中关键线路求解方法进行探讨，期望能够起到抛砖引玉的作用。

一、关键线路在项目管理中的主要应用

关键线路（Critical Path）又称关键路线，在项目管理中，关键线路具有最长的总工期并决定了整个项目的最短完成时间。关键线路是整个网络的瓶颈环节。任何关键线路上的任何延迟都将推迟整个项目的完成时间，即在关键路径上没有浮动时间。管理者应以关键线路上的关键活动为管理重点，调动企业资源，以期更好、更快地完成计划任务。具体而言，关键线路在项目管理中的主要应用有以下3个方面。

（一）基于关键线路进行项目进度管理

进度管理是项目管理的重要内容之一。基于关键线路对项目进度进行管理，这是人们研究关键线路的首要意义。所谓关键，那肯定是核心所在，相当于项目的命脉。项目建设中的工作数量越多、逻辑越复杂，关键线路的重要性就越大。这是因为，一方面，关键线路上的作业活动都是关键活动，这些活动决定了项目的最短完成时间，抓住了关键线路就是抓住了项目进度；另一方面，关键线路上的作业活动数量较少，抓住了关键的少数后，管理者们就可以充分配置有限的资源，做到有的放矢，将“好钢用在刀刃上”，节约资源。

（二）基于关键线路进行项目网络优化

基于关键线路主要可以实现两大网络优化。一是工期优化。因为项目工期是由关键线路决定的，所以可以通过调整关键线路上的施工方案，改变作业活动的逻辑关系，缩短关键线路的长度，从而缩短项目工期。这种网络优化，既缩短了工期，但又没有增加任何实质的投入。二是针对关键线路上的作业活动，有选择性地采用增加投入加快项目进度。只要增加的直接成本少于减少的间接成本，就可以实现网络的费用优化。

（三）基于关键线路进行项目索赔管理

项目实施其实就是执行合同的过程，或者说项目管理的过程就是合同管理的过程。在拟定项目合同的时候，由于认识的局限性和环境的不可预测性，不可能预测到项目实施过程中所有可能发生的情形。当项目在建设过程出现了合同中没有规定的事情的时候，就需要对合同进行调整，这往往就会产生索赔。索赔的内容主要就是工期和费用。在针对项目工期进行索赔的时候，关键线路就起到了重要的作用。如果干扰事件是关键线路上的，那么索赔的工期就是干扰事件发生的持续时间。如果干扰事件是非关键线路上的，那么索赔则只能针对超过了总时差的那一部分时间长度。

由此可见，关键线路在项目管理中具有举足轻重的作用。因此，准确求解关键线路，对开展项目管理具有十分重要的作用。

二、关于关键线路求解方法的思考——以一道习题为例

笔者在讲授“生产与运营管理”课程的时候，使用的教材《生产与运营管理》（第二版）是由陈荣秋、马士华编著，高等教育出版社出版的。该教材第十四章——项目计划管理后面附有一道这样的练习题[2]411：按表a提供的资料， （1）绘制节点型网络图和箭线型网络图；（2）在箭线型网络图上计算事件的时间参数；（3）计算活动的最早可能开工时间和最迟必须开工时间，求出关键线路。

表a 项目活动的基本信息

笔者结合本文的主题，在这里主要是探讨该道练习题中箭线型网络图的关键线路求解方法。

根据已知活动的紧后逻辑关系，按照箭线型网络图的绘制原则画出箭线型网络图，如下图a所示。其中，网络图中的两个虚箭线为虚活动，仅代表活动的先后关系，既不需要消耗时间，也不需要消耗其他资源。

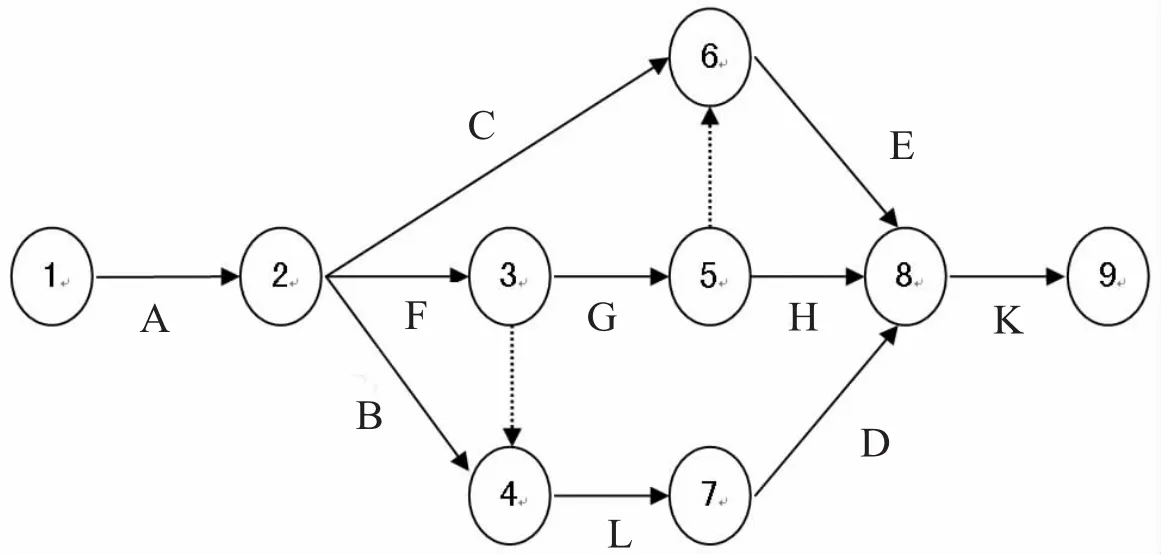
图a 箭线型网络图

常用的求解关键线路的方法主要有时差法、线路时间比较法、破圈法。下面分别运用这三种方法来求解该网络图的关键线路。

（一）基于时差法求解关键线路

该方法是对关键线路的定义的运用。陈荣秋、马士华（2005）等人均认为，从起始节点到终止节点顺序地将所有事件时差为零的节点连接起来的线路即为关键线路[2]387。于是，先计算出图a中各个节点的时间参数（事件最早可能发生时间ET（i），事件最迟必须发生时间LT（i））；再求出网络图中的关键节点，即时差S（i）为零（S（i）=（LT（i）-ET（i）=0）的节点；最后，从起始节点到终止节点顺序地将所有关键节点连接起来，所得到的线路即为关键线路。

网络图a中各个节点的时间参数如表b所示。其中，运用到的计算公式为：ET（i）=max{ET（i）+t（ i，j） }，LT（i） =min{LT（ i） -t（ i， j） }。式中，i和j分别代表箭尾时间和箭头时间；t（i，j）为活动（i，j）所需时间。由于网络图中的虚剪线只反映逻辑关系，不耗用时间和其他资源，因此，t（ 3， 4） =0， t（ 5， 6） =0。

表b 事件时间参数计算表

从表b计算的结果来看，这个网络图比较特殊，图中所有节点的时差均为0。也就是说，网络图中的9个节点均为关键节点。那么从起始节点①号节点到终止节点⑨顺序地将关键节点连接起来，多得到的任何一条线路都是项目的关键线路。显然，这道题目不仅是存在着多条关键线路，而且是每条线路都是关键线路。根据箭线型网络图的逻辑关系，我们一共可以连接出5条线路。按照时差法的计算结果，则这5条线路都是关键线路了，如表c所示。这些线路果真都是所求的关键线路吗？

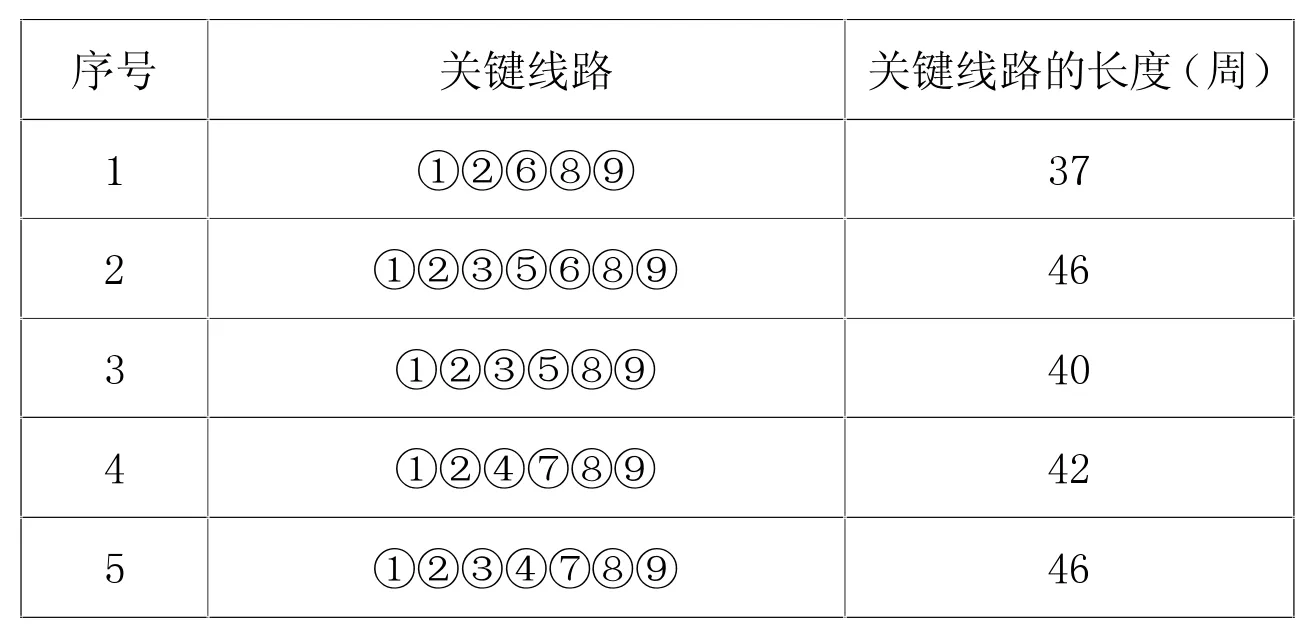
表c 基于关键线路定义求解出的关键线路

我们不妨将上述5条关键线路的长度求解出来，求解方法是对每条关键线路所包含的作业活动的作业时间求和。计算结果如表c所示。但是，这里所求解出来的关键线路的长度并不相同，最长为46周，最短为37周。关键线路的性质告诉我们，关键线路的长度决定了整个工期的长度，线路中各种活动的时间之和一定是最大的[2]390。因此，如果有多条关键线路的话，那么所有关键线路的长度应该是相等的，并且是所有线路中长度最大的。然而，表c的计算结果显然与此相矛盾。莫非这5条关键线路并非都是关键线路？我们运用其他方法来求解看看结果如何。

（二）基于线路时间比较法求解关键线路

该方法是对网络图中关键线路最长这一特性的运用。首先，找出网络图中所有可能的线路；然后，计算出这些线路的长度，其中时间最长的即为关键线路。先列出网络图a中包含的所有线路，共有表c中所列示的5条。既然，关键线路最长，根据这5条线路的长度来看，只有第2条和第5条线路，才是真正意义上的关键线路，它们的长度都为46周，为这5条线路中的最大值，也就是该项目的工期。而第1条、第3条、第4条线路只是伪关键线路。真的是这样吗？我们且看看第三种方法的求解结果。

（三）基于破圈法求解关键线路

这一方法比较实用，而且简便易行，它不需要求时间与时差，而可以直接根据画出的网络图进行分析，并且很快就可以找出关键的线路。具体方法如下： 在网络图中，如果从某一个结点到另一个结点之间存在着两条或两条以上不同的线路，便形成了一个封闭的环，称之为圈。如果这两条线路的时间不相等，则删去线路时间较短的线路，保留下来作业时间较长的线路， 即破圈；如果这两条线路的时间都相等，则破圈时，要把两条线路同时保留下来。把所有的圈都破除后，剩下的首尾连接的线路就是关键线路。破圈时应坚持从前向后，从内向外的顺序进行。

具体到网路图a，求解过程如下： （1）从节点②到节点④存在着两条线路：②④和②③④，其中线路②④要短于线路②③④，所以首先将②④破掉。（2）依此类推，活动H、活动C先后被破除。从节点③到节点⑧存在着两条线路：③⑤⑧和③④⑦⑧，其中③⑤⑧线路要短，于是活动G被删除。（3）至此，所有圈均被破除，剩下两条线路①②③⑤⑥⑧⑨和①②③④⑦⑧⑨，其长度均为46，即为该网络图的关键线路，如下图b所示。

图b 破圈法求解关键线路示意图

显然，破圈法求解出来的关键线路与线路时间比较法所求解出来的结果是相同的，并且这两条线路上节点时差都为零，也都是网络图中最长的线路，完全符合“关键线路至少有一条，可能有多条”和“关键线路所有活动时差均为零，没有任何缓冲余地”的特征[2]390。从另一个角度来讲，时差法并不适用于这道练习题。

笔者所用教材中的这道练习题比较特殊，就是网络图中所有的节点的时差都为零。但是由于并不是每项活动所需要的时间都相等，网络图中的线路长度肯定是有差异的，因此，基于时差法所得出的所有线路都是关键线路的结论肯定是站不住脚的。我们反过来看运用线路时间比较法和破圈法所求解出来的两条关键线路①②③⑤⑥⑧⑨和①②③④⑦⑧⑨，恰好涵盖了网络图中的9个节点。这道练习题反映出由时差为零的节点所连接形成的线路不一定是关键线路，但是关键线路上节点的时差一定为零。可见，节点时差为零并不是判断关键线路的充分条件，而只是必要条件。

三、结论

关键线路是整过网络的瓶颈环节。求解关键线路对科学开展项目管理具有重要意义。但是，在时差法、线路时间比较法和破圈法这三种求解箭线型网络图常用方法中，时差法并不适用于所有节点时差均为零的这一特殊网络图。节点时差为零只是关键线路的必要条件，而非充分条件。在求解关键线路的时候，线路时间比较法和破圈法相对而言更加准确可靠。

[1]杨青.关键线路在工程网络计划中的作用及确定[J].山西煤炭管理干部学院学报,2010（2）.

[2]陈荣秋,马士华.生产与运作管理[M].北京:高等教育出版社,2005.

F224.33

A

1673-8535（2011）02-0095-05

2011-01-20

新世纪广西高等教育教学改革工程“十一五”第4批启动项目（2008CD82）阶段性成果

朱良华（1980-），男，湖北仙桃人，梧州学院讲师、经济师，企业管理硕士，主要研究方向：人力资源管理。

高 坚）