磁层顶日下点距离R0与磁暴Dst指数的相关性
程国胜,苑顺周,赵蕾
(南京信息工程大学数理学院,江苏南京210044)
磁层顶日下点距离R0与磁暴Dst指数的相关性
程国胜,苑顺周,赵蕾
(南京信息工程大学数理学院,江苏南京210044)
利用2004—2006年ACE、WIND卫星观测的太阳风数据和相应时期反映磁暴大小的Dst指数,针对200个不同级别的磁暴事件,分析了磁层顶日下点距离R0与磁暴Dst指数的线性相关性。分析显示,在极端太阳风条件下,Dst指数时间序列比借助于Chao Model计算出的磁层顶日下点距离R0的时间序列延迟了约3 h。经修正时间延迟后,对磁层顶日下点距离R0与磁暴Dst指数的线性相关性进行分析。结果表明:发生超级磁暴时,二者线性相关系数的均值为0.77;大磁暴时,线性相关系数的均值为0.74;中等磁暴时,线性相关系数的均值为0.47。此外,用最小二乘数据拟合得到了不同级别磁暴时的R0-Dst关系图。
磁层顶日下点距离;磁暴;线性相关系数;最小二乘拟合方法
0 引言
磁层顶是磁层与太阳风等离子体的边界,决定着磁层的形状,所以磁层顶的位置参数在空间天气研究中有着至关重要的作用。Chapman and Ferraro(1931)根据太阳风动压与磁层磁压的平衡,首次提出磁层顶边界的存在;随后,Ferraro(1952)描述了磁层顶的形状。Aubry et al.(1970)注意到,行星际磁场的强度大小和方向也会影响磁层顶到地球的距离。随着科技发展,人们采集的卫星数据越来越多,越来越精确,一些空间物理学家们借助于已有数据分析,提出了多个磁层顶模型(Holzer and Slavin,1978;Sibeck et al.,1991;Roelof and Sibeck,1993;Shue et al.,1998;Boardsen et al.,2000;Kalegaev and Lyutov.,2000;Chao et al.,2002),模拟了在不同太阳风条件下的磁层顶位置。通常太阳风条件下,磁层顶日下点距离R0大约有10RE~11RE(地球半径);太阳风条件极弱时,R0可达14RE;极端太阳风条件时,磁层顶日下点会被压缩到地球同步轨道以内,即R0小于6.6RE(Kuznetsov and Suvorova,1998)。Plaschke et al.(2009)给出了磁层顶运动的统计分析研究。Yang et al.(2002)发现PR96模型(Petrinec and Russell,1996)、Shue98模型(Shue et al.,1998)和C02模型(Chao et al.,2002)适合应用于模拟极端太阳风条件下磁层顶位形,其中C02模型能够更好的预测极端太阳风条件下的磁层顶穿越事件。
磁层中的环电流是赤道面附近围绕地球的一个环形电流带,其主体部分是西向电流,磁暴期间总强度可达几百万安培,因而引起地球磁场水平分量大幅度减小。然而,磁层顶日下点距离与磁层顶电流有关,根据等离子体物理的单粒子理论可知,磁层顶电流是由太阳风等离子体产生的一种抗磁电流,亦会引起地球磁场水平分量减小。扰动一般限于高纬极区,但在行星际磁场具有长期的南向分量且具有较大的幅度(大于10~15 nT)时,磁层连续受到压力,磁场扰动到达赤道区域。在中低纬度的测站使用的每一小时量测地磁扰动强度的一种分级指标,称之为Dst指数,主要是量测地磁水平分量强度变化的一种物理量。Dst指数是研究磁暴期间磁场扰动特征的一个关键参数,对分析地磁场活动有重要的作用(刘振兴和濮祖荫,1997),通常Dst<-200 nT为超级磁暴,-200 nT≤Dst<-100 nT为大磁暴,-100 nT≤Dst<-50 nT为中等磁暴,-50 nT≤Dst<-30 nT为小磁暴(Gonzalez et al.,1999)。同时,太阳风动压和行星际磁场是预测磁暴模型的主要输入值(Wei et al.,2007),也是日侧磁层顶位置的主要影响因素,因此磁层顶日下点距离与磁暴指数之间必然存在某种关系。Shue et al.(2000)比较了低纬磁层顶位形模型后发现,众多模型只考虑磁层顶位置变化受外在因素的影响,而没有考虑磁层顶位置是否与磁层磁暴活动有关联的问题。
针对Shue提出的上述问题,迄今还未见到相关的研究。本文利用卫星观测到的数据,对磁层顶日下点距离与磁暴指数之间的关系进行了统计分析。通过比较PR96、Shue98和C02模型所得的R0,发现C02模型更适合用来计算磁层顶日下点距离R0。利用2004年ACE、WIND卫星提供的太阳风流和行星际磁场数据,基于C02模型,分析了不同级别磁暴发生时R0-Dst的相关性;然后,利用2005—2006年相应数据,对所得结论进行验证,发现在发生不同级别磁暴时,R0-Dst之间存在着线性相关性,磁暴越强,线性相关性越大。最后,按磁暴级别,对2004—2006年200个磁暴事件进行统一处理,得到在超级、大、中等磁暴发生时线性相关系数的均值分别为0.77、0.74、0.47,并用最小二乘拟合得到不同级别磁暴时的R0-Dst关系式。
1 数据
所用的太阳风参数和行星际磁场的数据来源于ACE、WIND卫星,分辨率为1 h。在GSM(geocentric solar magnetic system)坐标系下,行星际磁场(IMF)的南向分量Bz、太阳风速度Vsw和密度Nsw数据主要来自ACE卫星,对ACE卫星缺失的数据通过WIND卫星数据进行补充。实时的地磁Dst指数数据来自于WDC(World Data Center for geomagnetism,Kyoto),分辨率为1 h。以上资料均取自NASA的Space Physics Data Facility(SPDF)网站(http://cdaweb.gsfc.nasa.gov/cnofs/)。
2004年太阳活动极为频繁,存在不同级别的磁暴,数据比较完整。根据磁暴级别定义进行统计可知,2004年的82个磁暴,有小磁暴54个、中等磁暴22个、大磁暴5个和超级磁暴1个。利用2005—2006年的118个磁暴(小磁暴76个、中等磁暴31个、大磁暴10个和超级磁暴1个)发生时的数据对2004年的结论进行验证。
2 日侧磁层顶模型比较
在众多的磁层顶位置模型中,大都体现了磁层顶的物理过程,并把这些物理过程转化成为数学模型(Russell,2003)。例如,磁层顶日下点距离对于太阳风压力的指数依赖性体现了磁偶极场的性质;磁层顶日下点距离对IMF Bz的非线性依赖性体现了磁层顶侵蚀的非线性饱和。大部分磁层顶位置模型应用的是通常太阳风条件下磁层顶穿越事件的数据(Dmitriev et al.,2005),而模型用在极端太阳风条件下时需要进一步考虑。PR96模型、Shue98模型和C02模型是拟合磁层顶位置较为合适的模型(Yang et al.,2002)。下面分别介绍这3种模型的日侧部分。
2.1 日侧PR96模型
PR96模型的向阳一侧假设磁层顶关于XGSE(geocentric solar ecliptic system)轴旋转对称,且地心与椭圆交点重合,使用的是XGSE≥-10RE空间范围内低纬磁层顶穿越数据,给出向阳侧磁层顶位形模型如下:
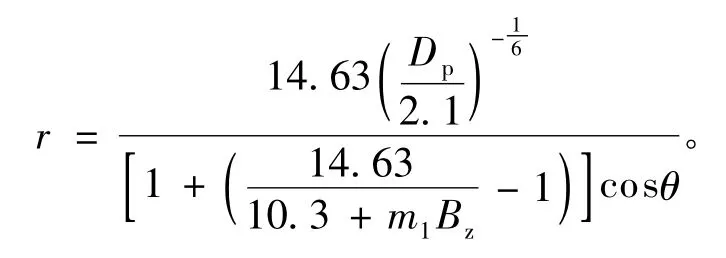
其中:IMF北向时,m1=0;IMF南向时,m1=0.16。这里r代表磁层顶的径向距离,θ是太阳的天顶角;当θ=0时,r=r0代表日下点距离。
2.2 日侧Shue98模型
在处理上游太阳风数据时,采用固定太阳风传输时间,结合ISEE和IMP 8卫星的数据,Shue98模型采用方程
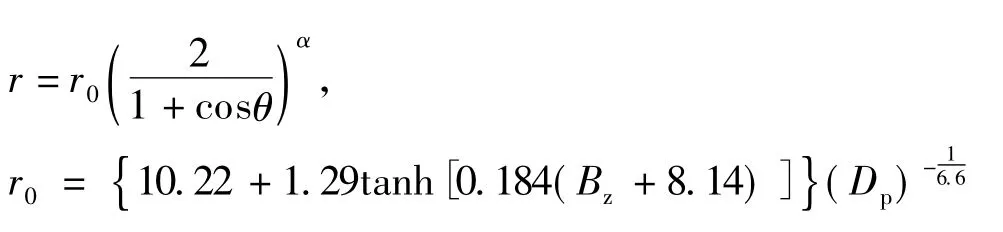
描述了磁层顶的位置和形状。其中:地球作为原点;r代表磁层顶的径向距离;θ是太阳的天顶角;参数r0和α分别代表磁层顶日下点距离和磁层顶张角。
2.3 日侧C02模型
C02模型采用了Shue98模型方程,且用分段函数来描述不同太阳风条件下磁层顶位形。假设在通常和极端太阳风条件下模型具有相同的表达式,r0的具体表达式为:

在通常太阳风条件下(r0≥7.0RE),推导出的系数为:a1=11.646,a2=0.216,a3=0.122,a4=6.215;在极端太阳风条件下(r0≤6.4RE),推导出的系数为:a1=11.646,a2=0.169,a3=0.158,a4=6.800;如果6.7RE<r0<7RE,则ln(r0)-ln(7)=c1(Dpc2);如果6.4RE<r0<6.7RE,则r0-6.4=c3(Dpc4)。由于r0和在r=7R处以及r=6.4R处连续,可分别求出c1和c2以及c3和c4。
2.4 模型的比较
下面将2004年4月的前40 h数据应用于PR96、Shue98和C02模型,分别计算磁层顶日下点距离,然后进行比较(图1)。
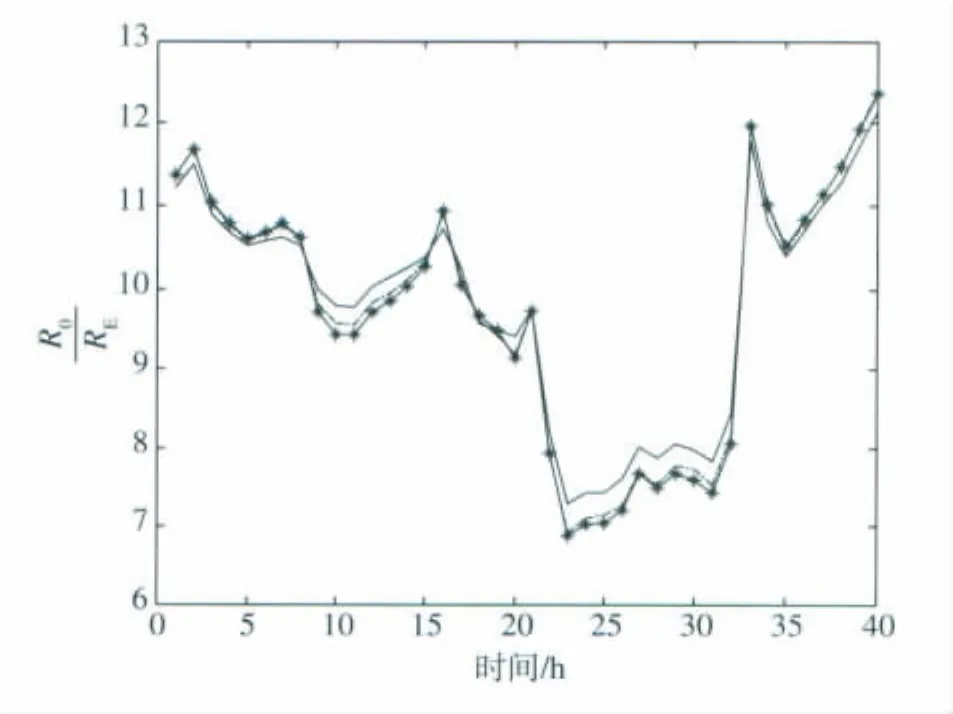
图1 PR96、Shue98和C02模型所计算的磁层顶日下点距离R0的比较(虚线:PR96;实线:Shue98;星形线:C02)Fig.1 Comparison of R0calculated by PR96,Shue98 and C02 models,respectively(The dash line:PR96;the solid line:Shue98;the asteroid line:C02)
Yang et al.(2002)对3种模型进行比较后发现,C02模型能够更好地预测极端太阳风条件下的磁层顶穿越事件。图1显示,3种模型在通常太阳风条件下区别不大,而在极端太阳风条件下区别明显,其中C02模型能够更好地描述磁层顶日下点位置。基于上述原因,本文采用C02模型来计算磁层顶日下点距离R0。
3 R0-Dst的相关性
下面分别考虑2004年的82个磁暴(超级磁暴1个、大磁暴5个、中等磁暴22个和小磁暴54个)的Dst指数与磁层顶日下点距离R0的相关性。在用计算R-D之间的相关系数后,得出不同级别磁暴情况下的线性相关系数均值。
3.1 超级磁暴
对2004年太阳风数据流和地磁指数数据进行统计分析,只找到2004年11月7—18日发生的一个超级磁暴。通过对此次磁暴Dst指数时间序列和R0时间序列比较发现,磁暴Dst指数时间序列比磁层顶日下点距离的时间序列延迟了约3 h。修正时间延迟后,磁暴Dst指数极小值与磁层顶日下点距离R0的极小值有明显的对应。图2给出了修正时间延迟后磁层顶日下点距离R0与磁暴Dst指数的对比。
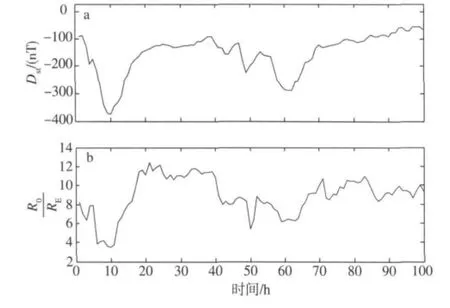
图2 修正时间延迟后的磁暴Dst指数与磁层顶日下点距离R0的对比Fig.2 Contrast between Dstindex and magnetopause standard off distance R0after the lag time corrected
比较图2a与2b发现,在这次超级磁暴中随着时间的变化,磁暴Dst指数和磁层顶日下点距离R0的变化曲线趋势一致。进一步考虑Dst指数和R0之间的相关性,得到二者线性相关系数的均值是0.762。图3给出了对此次超级磁暴266个R0-Dst数据集用最小二乘拟合方法得到的结果(直线为最小二乘拟合得到的结果;方程式y=0.018x+11是拟合关系式)。

图3 超级磁暴期间Dst指数和磁层顶日下点距离R0的线性拟合Fig.3 The linear fitting between Dstindex and magnetopause standard off distance R0during the super storm
3.2 大磁暴
统计分析2004年太阳风数据流和地磁指数数据,一共有5个大磁暴。大磁暴发生时R0-Dst之间的线性相关系数均值为0.724(表1)。

表1 5个大磁暴发生时R0-Dst之间的线性相关系数Table 1 The linear correlation coefficients of R0-Dstduring 5 big storms,respectively
下面研究这5个大磁暴。对每个磁暴发生时Dst指数的时间序列和R0的时间序列进行了对比分析,发现把Dst指数时间序列延迟R0时间序列3 h的情况下,它们之间相关系数最高;而延迟2 h或4 h的情况下,相关系数会明显下降。因此得到结果如下:大磁暴发生时,磁暴Dst指数的时间序列比R0的时间序列延迟了约3 h。修正时间延迟后,Dst指数与R0变化曲线趋势一致。进一步对所有大磁暴事件的303个R0-Dst数据集,用最小二乘拟合方法进行拟合。图4表示的是大磁暴事件Dst指数和R0的线性拟合结果(拟合得到的函数关系式是y=0.028x+12)。
3.3 中等磁暴
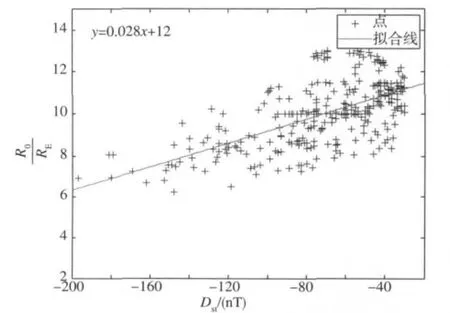
图4 大磁暴期间Dst指数和磁层顶日下点距离R0的线性拟合Fig.4 The linear fitting between Dstindex and magnetopause standard off distance R0during big storms
现在考虑2004年22个典型的中等磁暴,如表2所示。可见,中等磁暴发生时,R0-Dst之间的线性相关系数均值为0.453 4。分析这22个中等磁暴,对每个磁暴发生时Dst指数的时间序列和R0的时间序列进行了对比分析,发现把Dst指数时间序列延迟R0时间序列3 h的情况下,它们之间相关系数最高;而延迟2 h或4 h的情况下,相关系数会明显下降。因此得到结果如下:中等磁暴发生时,磁暴Dst指数时间序列比R0的时间序列也延迟了约3 h。修正时间延迟后,磁暴Dst指数和磁层顶日下点距离R0的变化曲线具有相当程度的一致性。
进一步利用所有中等磁暴事件的587个R0-Dst数据集,用最小二乘线性拟合方法进行拟合。图5表示的是中等磁暴事件Dst指数和R0之间的线性拟合结果(拟合得到的函数关系式是y=0.027x+11)。
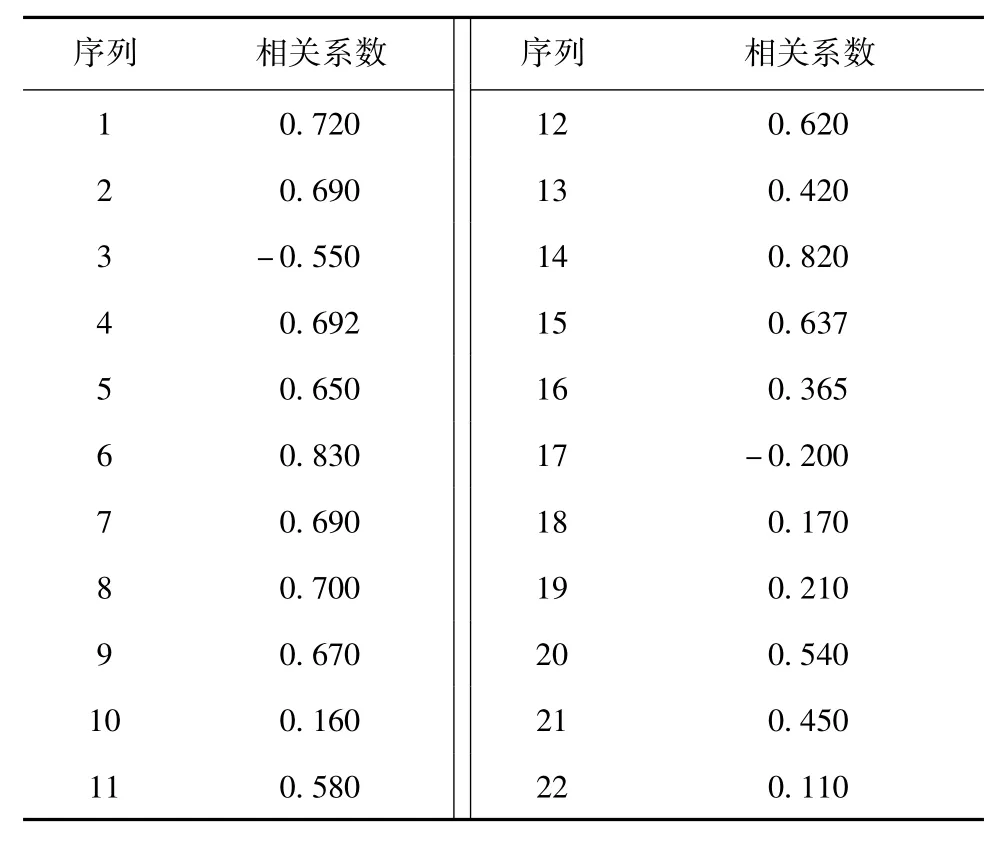
表2 22个中等磁暴发生时R0-Dst之间的线性相关系数Table 2 The linear correlation coefficients of R0-Dstduring 22 middle storms,respectively
对2004年的54个小磁暴进行研究。结果显示,小磁暴发生时R0-Dst之间的线性相关系数均值仅为0.24左右,因此小磁暴事件发生时,Dst指数和R0之间没有明显的线性相关性。
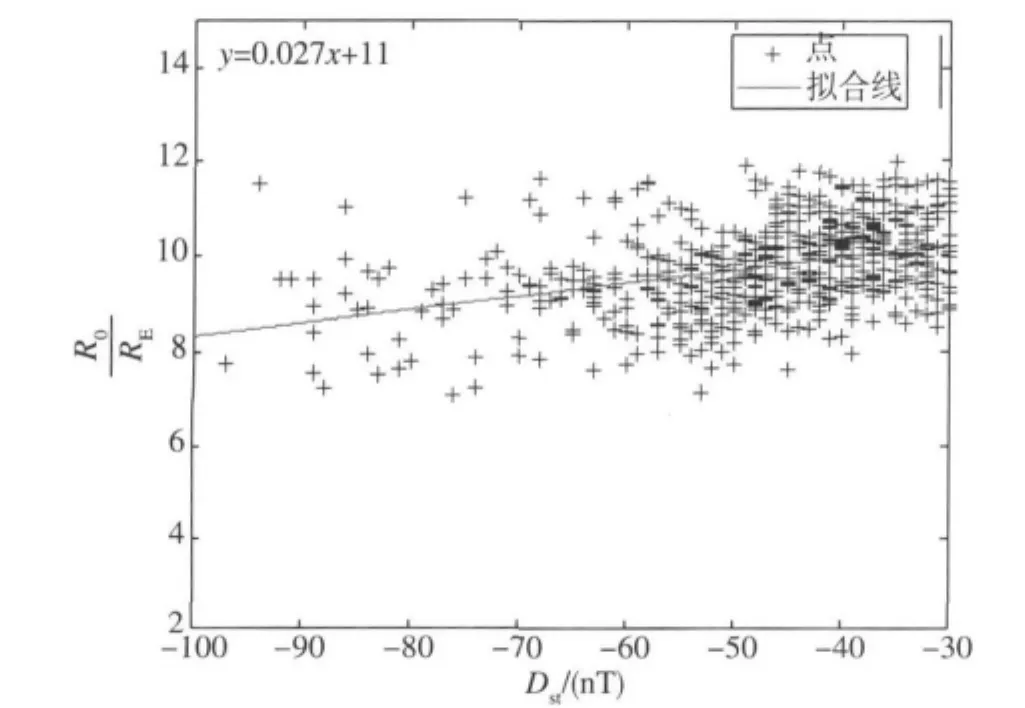
图5 中等磁暴期间Dst指数和磁层顶日下点距离R0的线性拟合Fig.5 The linear fitting between Dstindex and magnetopause standard off distance R0during middle storms
4 验证与讨论
根据上节分析发现,在磁暴发生时R0-Dst之间存在着线性相关性,磁暴级别越强,线性相关性越大。那么,这个结果是否具有普适性呢?针对这个问题,用2005—2006年118个不同级别磁暴数据,对上述结论进行验证,处理方法与上节类似,结果见表3。表3显示,2005—2006年R0-Dst之间平均相关系数与2004年的结果相近,误差值都在0.05以内;在超级磁暴、大磁暴、中等磁暴和小磁暴发生的情况下,误差率分别为1.3%、5.5%、9.1%和8.2%。由此得出结论:在发生不同级别磁暴时,R0-Dst之间确实存在着线性相关性,且级别越强,相关性越大。
最后,将2004—2006年200个不同级别磁暴事件统一进行处理。对表3中2004年和2005/2006年二者的平均相关系数取均值,得到如下结果:发生超级磁暴时,R0-Dst线性相关系数均值为0.77;发生大磁暴时,R0-Dst线性相关系数均值为0.74;发生中等磁暴时,R0-Dst线性相关系数均值为0.47。
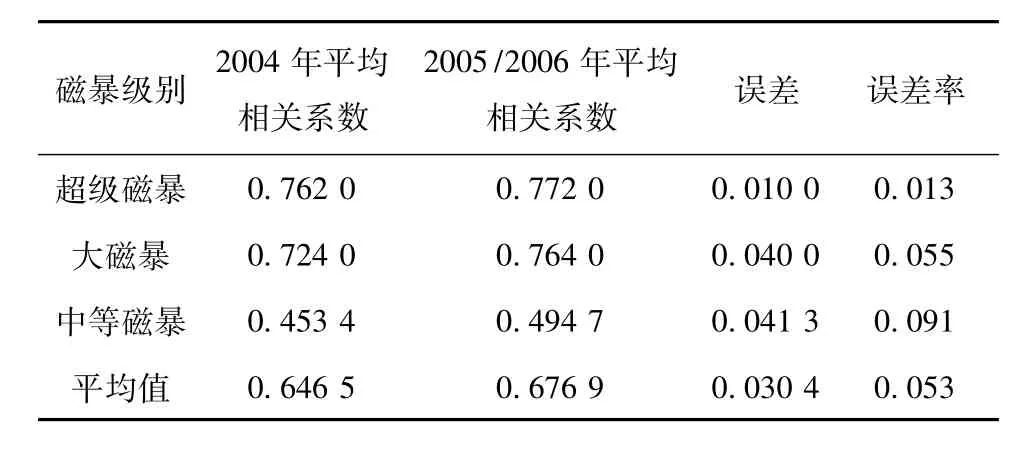
表3 2004与2005/2006年R0-Dst之间平均相关系数的比较Table 3 Comparison of the average correlation coefficients in 2004 and 2005/2006
5 结论
本文利用C02模型得到极端太阳风条件下的磁层顶日下点距离R0,对R0与磁暴Dst指数进行相关性分析后发现,两者存在约3 h的延迟,也就是说,从太阳风激波突然压缩磁层顶到影响磁层电流体系(主要包括磁层顶电流和环电流)产生抗磁效应所需要的时间大概为3 h。修正时间延迟后R0-Dst之间存在着线性相关性,磁暴级别越强,线性相关性越大,且得到了不同级别磁暴时的R0-Dst拟合关系。
本文结果将为研究磁暴活动提供了一个新途径,有助于认识太阳风—磁层耦合过程。R0-Dst的线性相关性研究,为研究磁层顶位置和磁暴活动提供了一个新思路,使得通过磁层磁暴活动强度大小来反演日侧磁层顶位置的远近成为可能。对此问题,我们将进行后续研究。另外,伴随着Cluster、THEMIS等卫星的升空,空间物理学家已经对磁层顶位置进行动态研究(Zhang et al.,2009);以前大部分模型把磁层顶的位置看作仅仅依赖于上游太阳风和行星际磁场,事实上,随着上游太阳风环境的改变,导致了磁层顶的位置在平衡态附近来回震荡。考虑磁层顶运动速度时,磁层顶位置变化与磁暴的关系有待进一步研究。
致谢:对提供帮助的中国科学院空间科学与应用研究中心王赤研究员,台湾国立中央大学太空科学研究所Jih-Kwan Chao(赵寄昆)教授,及提出建设性修改意见的审稿人,一并表示衷心感谢!
刘振兴,濮祖荫.1997.我国磁层物理研究的进展和展望[J].地球物理学报,40(增刊):7-19.
Aubry M B,Russell C T,Kivelson M G.1970.Inward motion of the magnetopause before substorm[J].J Geophys Res,75(34):7018-7031.
Boardsen S A,Eastman T E,Sotirelis T,et al.2000.An empirical model of the high-latitude magnetopause[J].J Geophys Res,105(A10):193-219.
Chao J K,Wu D J,Lin C H,et al.2002.Models for the size and shape of the earth's magnetopause and bow shock[C]//Lyu Ling-Hsiao.Cospar Colloquia series Vol.12:Space weather study using multipoint techniques.Pergamon:Elsevier Science Ltd.:127-134.
Chapman S,Ferraro V C A.1931.A new theory of magnetic storm:1.The initial phase[J].J Geophys Res,36(77/79):171-186.
Dmitriev A,Chao J K,Thomsen M,et al.2005.Geosynchronous magnetopause crossings on 29—31 October 2003[J].J Geophys Res,110,A08209,doi:10.1029/2004JA010582.
Ferraro V C A.1952.On the theory of the first phase of a geomagnetic storm:A new illustrative calculation based on idealized(plane not cylindrical)model field distribution[J].J Geophys Res,57(1):15-49.
Gonzalez W D,Tsurutani B T,Cluade A L.1999.Interplanetary origin of geomagnetic storms[J].Space Science Reviews,88(3):529-562.
Holzer R E,Slavin J A.1978.Magnetic flux transfer associated with expansions and contractions of the dayside magnetopause[J].J Geophys Res,83(A8):3831-3839.
Kalegaev V,Lyutov Y G.2000.The solar wind control of the magnetopause[J].Adv Space Res,25(3/4):1489-1492.
Kuznetsov S N,Suvorova A V.1998.An empirical model of the magnetopause for board ranges of solar wind pressure and Bz IMF[C]//Polar cap boundary phenomena.Netherlands:Academic Publishers:120-131.
Petrinec S M,Russell C T.1996.Near-earth magnetotail shape and size as determined from the magnetopause flaring angle[J].J Geophys Res,101(A1):137-152.
Plaschke F,Glassmeier K H,Auster H U,et al.2009.Statistical study of the magnetopause motion:First results from THEMIS[J].J Geophys Res,114,A00C10,doi:10.1029/2008JA013423.
Roelof E C,Sibeck D G.1993.Magnetopause shape as a bivariate function of interplanetary magnetic field Bzand solar wind dynamic pressure[J].J Geophys Res,98(A12):421-450.
Russell C T.2003.The structure of the magnetopause[J].Planetary and Space Science,51(1):731-744.
Shue J H,Song P,Russell C T,et al.1998.Magnetopause location under extreme solar wind conditions[J].J Geophys Res,103(A8):17691-17700.
Shue J H,Russell C T,Song P.2000.Shape of the low-latitude magnetopause:Comparison of models[J].Adv Space Res,25(7):1471-1484.
Sibeck D G,Lopez R E,Roelof E C.1991.Solar wind control of the magnetopause shape,location,and motion[J].J Geophys Res,96(A4):5489-5495.
Wei H L,Zhu D Q,Billings S A,et al.2007.Forecasting the geomagnetic activity of the Dst index using multiscale radial basis function networks[J].Adv Space Res,40(12):1863-1870.
Yang Y H,Chao J K,Lin C H,et al.2002.Comparison of three magnetopause prediction models under extreme solar-wind conditions[J].JGeophysRes,107(A1),1008,doi:10.1029/2001JA000079.
Zhang H,Zong Q G,Sibeck D G,et al.2009.Dynamic motion of the bow shock and magnetopause observed by THEMIS spacecraft[J].J Geophys Res,114,A00C12,doi:10.1029/2008JA013488.
Correlation between magnetopause standard off distance R0and geomagnetic storm Dstindex
CHENG Guo-sheng,YUAN Shun-zhou,ZHAO Lei
(School of Mathematics&Physics,NUIST,Nanjing 210044,China)
With the solar wind data observed by ACE/WIND spacecraft and the geomagnetic storm Dstindex data during 2004—2006,the linear correlation between magnetopause standard off distance R0and Dstindex,in which the grade of geomagnetic storm is characterized,is investigated in terms of 200 different graded storms.It is a fact that the time series of Dstindex lag about 3 h behind the time series of the magnetopause standard off distance R0calculated by Chao Model under the extreme solar wind.After the time lag corrected,the linear correlation between magnetopause standard off distance R0and geomagnetic storm Dstindex is revealed.The results show that the average linear correlation coefficients are 0.77,0.74 and 0.47,respectively,corresponding to the super,the big and the middle storms.Under different graded storms,the charts of R0-Dstfitted by the least square method are shown.
magnetopause standard off distance;geomagnetic storm;linear correlation coefficient;least square method
P353
A
1674-7097(2011)04-0504-06
2010-10-15;改回日期:2010-12-09
国家自然科学基金资助项目(60973157)
程国胜(1963—),男,安徽肥西人,博士,教授,研究方向为空间天气学、智能计算,chenggs@nuist.edu.cn.
程国胜,苑顺周,赵蕾.2011.磁层顶日下点距离R0与磁暴Dst指数的相关性[J].大气科学学报,34(4):504-509.
Cheng Guo-sheng,Yuan Shun-zhou,Zhao Lei.2011.Correlation between magnetopause standard off distance R0and geomagnetic storm Dstindex[J].Trans Atmos Sci,34(4):504-509.
(责任编辑:倪东鸿)

