基于加固边坡的可靠性分析设计抗滑桩锚固深度
张 松,吴坤铭,谭晓慧
(1.六安市农村公路管理局,安徽六安237000;2.皖西学院建筑与土木工程学院,安徽六安237012;3.合肥工业大学资源与环境工程学院,安徽合肥 230009)
基于加固边坡的可靠性分析设计抗滑桩锚固深度
张 松1,吴坤铭2,谭晓慧3
(1.六安市农村公路管理局,安徽六安237000;2.皖西学院建筑与土木工程学院,安徽六安237012;3.合肥工业大学资源与环境工程学院,安徽合肥 230009)
为了对抗滑桩锚固深度进行合理的设计,建立位移迭代有限元模型模拟桩-土间的相互作用,基于强度折减的位移迭代有限元法对边坡抗滑桩加固工程进行可靠性分析,把计算参数视为随机变量考虑参数变异性对抗滑桩锚固深度及边坡加固工程可靠性的影响。可靠指标的选取应考虑边坡工程等级,以目标可靠度为控制指标去指导抗滑桩锚固深度的设计。工程算例表明采用可靠性方法设计抗滑桩锚固深度是合理的,具有一定的工程应用价值。
位移迭代;有限元法;强度折减原理;可靠性分析
目前边坡抗滑桩加固工程设计及稳定性分析多为定值法。定值法经长期工程实践证明是一种有效的方法,但该方法最大的缺点是没有考虑实际存在的不确定性影响。实际上影响边坡抗滑桩加固工程的诸多因素中,绝大部分都表现为较强的随机性,如岩土体物理力学参数、桩-土间相互作用等。
锚固深度是边坡抗滑桩加固工程设计的重要指标之一。工程中一般先根据经验初步确定锚固深度,然后根据滑面以下桩的最大横向压应力小于或等于地基横向容许承载力的条件进行验算[1](P1-38),计算时均把各计算参数当作定值来处理。如蒋建国等[2]基于文献[1]的地基横向应力的容许值,推导了刚性桩锚固深度的计算公式,该公式在推导中进行了简化,影响了公式的精度和可靠性;张文居等[3]以文献[1]中桩身锚固深度的确定方法为基础,基于蒙特卡罗模拟法建立了刚性桩可靠度分析模型;胡晓军等[4]以强度折减安全系数为基础给出了刚性桩锚固深度的确定方法,该方法用确定性模型处理不确定性问题,仍属定值法。
鉴于此,本文建立位移迭代有限元模型模拟桩-土间的相互作用,基于强度折减的位移迭代有限元法对边坡抗滑桩加固工程进行可靠性分析,以目标可靠度为控制指标以确定抗滑桩锚固深度。
1 位移迭代有限元法
抗滑桩加固边坡传统设计理论[5-8]中所采用的许多假设都不同程度地回避了桩-土间相互作用的全面分析。所以建立一种抗滑桩与滑坡土体相互作用动态过程的设计计算方法,对工程的安全经济尤为重要。因此,本文建立位移迭代有限元模型模拟桩-土间的相互作用。
位移迭代有限元法的实质:以实体单元模拟岩土体,梁单元模拟抗滑桩,从而建立二维平面应变位移迭代有限元模型;有限元模型中梁单元抗滑桩的节点和实体单元在抗滑桩接触处的节点是公共的,通过梁单元抗滑桩的水平位移迭代计算来控制计算结果。
1.1 位移迭代有限元模型
抗滑桩治理滑坡如图1所示,为分析该滑坡桩-土相互作用体系,采用位移迭代有限元模型如图2所示,将整体模型分为桩后土体A、抗滑桩B和桩前土体C三部分。A、B、C三个子计算模型的综合即为抗滑桩与土体相互作用的位移迭代有限元模型。

图1 桩-土相互作用体系

图2 位移迭代有限元模型
1.2 位移迭代有限元法计算步骤
(1)建立子模型的有限元方程

其中,[K]为总刚度矩阵;{δ}为节点位移列阵;{R}为节点荷载列阵;上标A、B、C表示不同模型。
(2)将式(1)的三个方程按位移向量重组,使桩-土共节点处的水平位移集中在一起,并对刚度矩阵和荷载列阵分块,即

其中,{δAC}为A、B、C共节点的位移;{RAB}、{RCB}分别为A对B的作用力,C对B的作用力;{δA}、{δC}为{δAC}以外的各节点位移分量列阵;{RA}、{RC}分别为{δA}、{δC}对应的节点荷载;为各模型总刚度矩阵的子块。
(3)假定桩孔开挖瞬间完成,有限元迭代计算的初始条件设定为桩后和桩前土体不变形,即{δAC}0=0,代入式(2)、(4),可分别求得岩土体各节点的水平约束力{RAB}0、{RCB}0。
(4)将{RAB}0、{RCB}0作为边界条件作用于桩上,并代入式(3),可求得抗滑桩各约束节点的位移{δAC}1。
(5)将{δAC}1代入式(2)、(4),求得与该位移相应的岩土体各节点水平约束力{RAB}1、{RCB}1。
(6)将{RAB}1、{RCB}1代入式(3),求得与该土压力相应的抗滑桩各约束节点的位移{δAC}2。
(7)按下式(5)计算抗滑桩各约束节点位移的相对误差ε,若ε满足给定精度要求,则结束迭代计算;若ε不满足给定精度要求,重复第(5)~第(7)步,直至满足要求为止。相对误差ε精度由工程要求确定。

2 抗滑桩加固边坡的可靠性分析
由于位移迭代有限元模型能模拟桩-土间相互作用的动态变形协调过程,且有限元法具有不受边坡几何形状和材料不均匀限制的优点。因此,本文提出基于强度折减的位移迭代有限元法对边坡抗滑桩加固工程进行可靠性分析。
为了对文中方法及程序的合理性进行验证,本文采用验算点法计算可靠度指标,把计算参数视为随机变量考虑参数变异性对可靠指标的影响。以下给出验算点法基本求解过程。
设结构中存在n个互相独立的正态随机变量X1,X2,…,Xn,其均值为,均方差为。当结构功能函数为非线性函数时,为计算可靠度指标,将功能函数在验算点处展开。假定验算点x*=(x,…,)是已知的,则结构功能函数的一次展开式为:

实际上验算点x*=(,…)是未知的,需要用下述条件进行迭代计算:

(1)列出极限状态条件,并确定所有基本变量Xi的分布类型和统计参数μXi及σxi。

(3)由式(7)计算可靠指标β。
(4)由式(9)计算方向余弦αxi。

(6)若前后两次迭代计算满足式(10)的条件(ε规定的允许误差),则停止迭代;否则,取x*(0)=x*(1),转至第(3)~第(6)步继续进行迭代直至满足要求为止。

3 工程实例
安徽六霍公路某段,如图3,上层滑体组成物质主要为粘土,下层滑床为泥质岩,土体参数如表1。滑坡体为粘性土,其滑坡推力设为均匀分布。若该边坡设计安全等级为三级,延性破坏对应的可靠度指标β=2.7,安全系数FS=1.20,以稳定性分析为依据,拟采用抗滑桩进行加固。

图3 边坡剖面图

表1 土体参数表
(1)常规设计
采用单排抗滑桩加固,抗滑桩设置在距路堤24m处,桩体附近滑体厚度为5.0m。抗滑桩采用C30混凝土,弹性模量Ec=3×107kPa,泊松比v=0.2。桩截面为b×a=1.5m×2m,桩受荷段h1=5m,初选锚固深度h2=7.7m,桩间距l=3m。
由定值法计算此时边坡整体安全系数FS= 1.201,故初选锚固深度h2=7.7m满足设计要求。
(2)加固后边坡的可靠性分析
设φ、c、γ是互为独立的正态变量,E、v为定值,均值见表2,变异系数δ的取值见表3。采用验算点法计算加固后边坡的整体可靠度指标β,可靠指标对应的抗滑桩有效长度见表4。

表2 各计算参数的均值

表3 各计算参数的变异系数δ取值
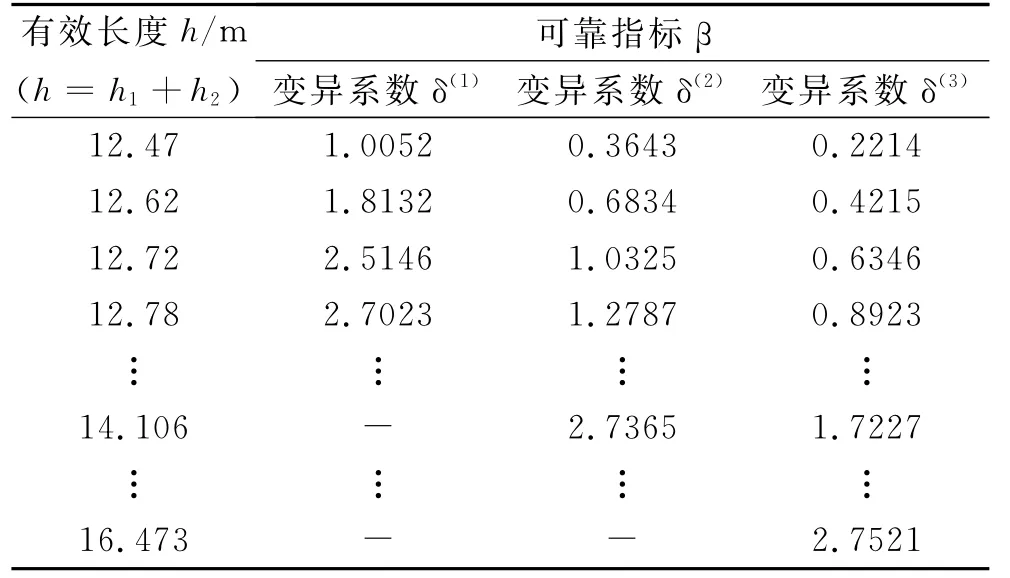
表4 可靠指标-抗滑桩有效长度表
由表4计算结果可知:
抗滑桩加固边坡的整体可靠指标随参数变异程度增大而减小。边坡的整体目标可靠指标β=2.7;由计算结果可知当变异系数取δ(1)时,β=2.7023,相应的锚固深度为7.78m(12.78m-5m=7.78m)、失效概率为3.4×10-3,传统强度折减有限元法可靠指标β=2.685,定值法安全系数FS=1.211,满足设计要求;当变异系数取δ(2)时,β=2.7365,相应的锚固深度为9.106m(14.106m-5m=9.106m)、失效概率为3.1×10-3,传统强度折减有限元法可靠指标β=2.7119,定值法安全系数FS=1.25,满足设计要求;当变异系数取δ(3)时,β=2.7521,相应的锚固深度为11.473m(16.473m-5m=11.473m)、失效概率为2.96×10-3,传统强度折减有限元法可靠指标β=2.7357,定值法安全系数FS=1.31,满足设计要求。
由上述分析可知:锚固深度取7.7m虽然能满足常规设计要求,却无法满足三级边坡可靠性要求。当计算参数变异程度不同时,抗滑桩锚固深度应作相应的调整;文中方法可靠指标计算结果与传统强度折减有限元法可靠指标计算结果相近,因而文中方法是准确的。因此,抗滑桩锚固深度的确定应将常规设计与可靠性分析相结合,考虑计算参数的随机性,以目标可靠度为控制指标去指导抗滑桩锚固深度的设计。
4 结论
(1)建立位移迭代有限元模型模拟桩-土间相互作用的动态变形协调过程,基于强度折减的位移迭代有限元法对边坡抗滑桩加固工程进行可靠性分析。
(2)可靠性分析时将计算参数视为随机变量,由算例分析可知,加固后边坡的整体可靠指标随参数变异程度增大而减小。
(3)常规设计中未考虑计算参数的随机性,而可靠性分析弥补了这一不足。因此,工程实践中应考虑边坡工程等级,以目标可靠度为控制指标考虑参数的变异性,逐步调整桩长使加固后边坡的整体可靠指标满足设计要求,以此确定抗滑桩锚固深度。
[1]铁道部第二勘测设计院.抗滑桩设计与计算[M].北京:中国铁道出版社,1983.
[2]蒋建国,邹银生,周绪红.刚性抗滑桩锚固深度的简化计算[J].工程力学,2001,(增):457-460.
[3]张文居,赵其华,刘晶晶.参数变异对抗滑桩锚固深度可靠度的影响[J].水文地质工程地质,2006,(3):61-63.
[4]胡晓军,王建国.基于强度折减的刚性抗滑桩锚固深度确定[J].土木工程学报,2007,40(1):65-68.
[5]Stwart D P,Jewell R J,Randolph MF.Design of Piled Bridge Abutments on Soft Clay for Loading From Lateral Soilmovments[J].Geotechnique,1994,44(2):277-296.
[6]王年香.被动桩与土体相互作用研究综述[J].水利水运科学研究,2000,(3):69-76.
[7]K X Liu,F H Lee,K Y Yong.Journal of Geotechnical and Geoenvironmental Engineering[J].International Journal for Numerical Methods in Geomechanics,2004,154:441-450.
[8]Bransby MF,Springman S M.3-D Finite Element Modeling of Pile Groups Adjacent to Surcharge Loads[J].Computer and Geotechnics,1996,19(4):301-324.
Design for Anchoring Depth of Anti-slide Piles Based on Reliability Analysis of Slope Reinforcement
ZHANG Song1,WU Kun-ming2,TAN Xiao-hui3
(1.Lu’anCityRuralRoadsAuthority,Lu’an237000,China;
2.CollegeofArchitectureandCivilEngineering,WestAnhuiUniversity,Lu’an237012,China;3.SchoolofResourcesandEnvironmentEngineering,HefeiUniversityofTechnology,Hefei230009,China)
To rational design the anchorage depth for rigid anti-slide piles,a calculated method of interaction process of the pilesoil is presented in this paper:the displacement iterative finite element method,research on reliability of slope reinforced by antislide piles based on the method of strength reduction theory with displacement iterative finite element method,the calculated parameters are regarded as random variables when considering the different values of random variable impact on the reliability of anchoring depth for anti-slide piles and reinforced slope.The classification of a slope project should be considered in selecting the reliability index,the target reliability as control index to guide the design for the anchoring depth of anti-slide.Examples show that the reliability analysis to design the anchorage depth of anti-slide piles is rational and useful for engineering applications.
displacement iteration;finite element methods;principles of strength reduction;reliability analysis
TU473
A
1009-9735(2011)05-0128-04
2011-05-04
国家自然科学基金项目(40972194);安徽高校省级自然科学研究计划项目(KJ2010B267)。
张松(1977-),男,安徽六安人,工程师,研究方向:道路桥梁工程;吴坤铭(1978-),男,安徽六安人,讲师,博士,研究方向:岩土力学可靠度;谭晓慧(1971-),女,安徽宣城人,教授,博士,硕导,研究方向:岩土力学可靠度。

