宏观干预与通货膨胀
孙中才
(中国人民大学农业经济系,北京 100872)
宏观干预与通货膨胀
孙中才
(中国人民大学农业经济系,北京 100872)
从G函数这个理论范式出发,构造出反映生产与金融并行的市场经济模型;并在局部均衡的意义上给定了相应的固定数量约束条件,从而将货币投入量或货币供给水平耦合到了模型之中,得到了可以进行货币使用量分析的初始结构。依据经济内在的固定替代弹性规律,计算出固定替代弹性矩阵,实际上就得出了经济运行的本底背景,置于该背景上的经济结构及其格局变化,便归于了增长率与约束条件相互独立变化的交叉效应结果。据此,通过实际观测货币数量的增长率与货币约束最小紧缩率之间存在的差距,陈述了通货膨胀的确切定义;再通过最小紧缩率的结构,分析出宏观干预的切入点和干预行为的陈述;最后计算出宏观干预的测度。
宏观干预;基准运行;固定替代弹性;通货膨胀
一、引 言
通货膨胀(Inflation)是现代经济的常见现象之一,早已引起经济学家的关注,并给出过重要的解释[1]。在现实经济生活中,它经常导致经济体运行出现紊乱,促使实际工作部门创造了一些指示器,专门用来标示通货膨胀的程度,还在经验中摸索出了能够有效表示通货膨胀危害深度的指数[2]14-17。 其中,CPI(Consumer Price Index,CPI)已经成为很有用的衡量工具,用它可以给出通货膨胀程度的临界值,并在经验中,人们认可了这些临界值所表征的通货膨胀危害[2]71-72。 资料表明,无论是从基本理论的意义来讲,还是从实际工作的经验来讲,关于通货膨胀的探索都取得了很深入的成果。
然而,随着经济核心理论实现了新的综合,新的理论范式成为科学思路的新起点,其便利性和精确性以及给人们提供的新概念,使得已有的关于通货膨胀的传统解释和经验手段都不得不接受更加严格的审视,以便得到更加真实的理论解释或批评,从而肯定或撇弃已有的经验性近似,而采取更加准确的概念和测度,令有关实际做法更加向着科学指导下的技术方向进展。[3]
已有的关于通货膨胀的理论和指示性测度,大多属于事实层面上的症状归纳[4],[5]。 在科学发展史上,人们容易看到,对照更加深入的理论,以往的概念通常是流行未必真实、实用未必正确;坚持了正确的逼近方向,但并未达到精确的程度,通常是很普遍的。至于流传很广、深得人心,却并非真实;很能调动思路、立时可以取得经验成果,然而却不符合科学原理的情况,在某些现时社会工作中,或者在文明程度和科学知识欠缺的环境下,也是屡见不鲜的。[6]
正如上文已经提到的,在最新经济理论范式诞生之前,也就是在G函数成为经济学理论核心的最新综合之前,虽然F函数已经为通货膨胀理论提供了令人瞩目的思想基础。但是,由于F函数本身还难以将金融市场与货币供给的关系统一在同一种模型里,某些经济规律还难以表达为一致的思想构成。缺乏理论表达的保证,必定阻碍着亟需的理论探索。
G函数的确立明显地改变了这样的局面[7]。其关键所在就是G函数克服了F函数的困难,为经济学理论的明确表达和有关规律的解释,提供了统一的模型,给定了更便利的初始陈述结构[8]。就我们所要分析的宏观干预与通货膨胀的关系来说,便明显地体现了这一点。
二、固定替代弹性与基准运行
设所考虑的经济为两个生产部门与一个金融部门所组成,固定数量约束分别为各自的市场需求数量,对生产部门的需求是商品数量,对金融部门的是货币数量。这样,在G函数的框架下得出:

式中,π(.)--利润函数,
p1--生产部门1的产品价格,
p2--生产部门2的产品价格,
p3---金融价格,
v1---生产部门1的产品需求数量,
v2---生产部门2的产品需求数量,
v3---货币的固定数量。
式(1.1)的 Jacobi向量为:

由式(1.2),可以得出式(1.1)的 Hessian 矩阵为:
式(1.3)中的各个元素体现了该经济体在运行过程中,各个因子之间在二阶微分水平上的相互作用。
由式(1.3)可以得出的替代弹性矩阵为:

从式(1.4)-(1.6)的结构可以看出,式(1.1)中各个因子的系数和影响因素的变化,均不会导致式(1.4)-(1.6)的结果随之变化。 也就是说,经济总量水平上的结构性变化,均不会引起替代弹性的变化。 例如,如果式(1.1)的结构变成了式(1.7),即:

这便是经济学所发现的固定替代弹性(Constant Elasticity of Substitution,CES)。它是一个自然法则。
替代弹性所表征的是两个对应量之间,一方增长百分之一,另一方可以减少(或者也增加)百分之几。反之亦然。另一方是减少还是增加,则由Hessian矩阵中所对应的元素的符号来决定,若为“+”,则是假替代,表示一方增长,另一方也是增长;若为“-”,则是真替代,表示一方增长,另一方是减少。而式(1.3)中各个元素的符号,又取决于式(1.2)中元素的定义,因为在式(1.2)中,对应的数量若为产出,其符号为“+”,若为投入,则符号为“-”。作为约束条件的固定数量,其符号一律为“-”,因此其一阶导数也为“-”,因而可以视为广义的投入。这样,可以看到,在式(1.2)中,符号相同的数量,它们之间的交叉效应,导致式(1.3)中相对应元素的符号是“+”的,致使相应的固定替代弹性是假替代,表示一方增长,另一方也增长。而式(1.2)中符号不相同的数量,它们之间的交叉效应,导致式(1.3)中相对应元素的符号是“-”的,致使相应的固定替代弹性是真替代,表示一方增长,另一方会减少。与F函数中所定义的替代相一致,在G函数中,广义的产出与产出、投入与投入之间的替代是假替代,实则是相互促进的增长,即为此长彼长、此消彼消的关系;只有产出与投入之间的替代才是真替代,是此长彼消或彼消此长的关系。
从式(1.4)-(1.6)的结构可以看出,经济体中各个因子的任何数值变化均不能传递到二阶微分水平的替代关系中去,这种关系是固定的内在比例关系。也就是说,经济运行实际上遵循着这样的规律,即在二阶微分水平上,或者说在加速发展的水平上,因子数量的比例是保持不变的,加速背景是固定的、均匀的,继续的加速变化只能是因子自身增长率的变化在起作用。式(1.7)表示的内容,以及据此得出的替代弹性结果表明,经济结构所具有的固定替代弹性是初始性给定的,是经济具有的内在基准状态,价格、技术,以及种种干预和外来作用,可能会影响到因子数量的增长率,却不会改变固定替代弹性的值。这意味着,对于一个增长的经济来说,其中各因子的增长变化,必然会传递到经济内部,并作用于其余因子,因为它们统一地联系在利润这个点上。然而,由于固定替代弹性矩阵的存在,令人们知道这种传递必定是规范、依照固定比例的,并且是按照给定途径的。这也令人们知道了,经济的增长是相对于不变基准的膨胀,平稳而持久地发展是由这个基准所给定的,是由在加速水平上不变的比例
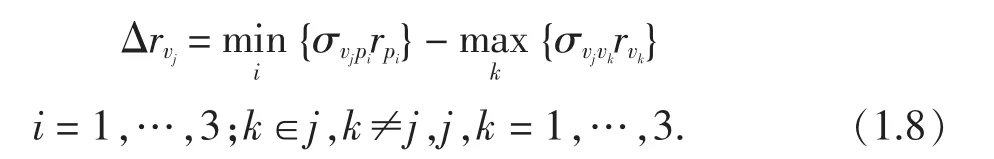
这里,Δrvj--约束条件vj的数量的被替代率;
σvjpi--约束条件vj与第i种产品之间的固定替代弹性值,i=1,…,3;j=1,…,3
rpi--第i种产品的价格增长率,i=1,…,3
σvjvk--约束条件vj与约束条件vk之间的固定替代弹性值,k≠j,j,k=1,…,3;关系所决定的。
在报酬递减率的研究中,经济学家们首先发现了因子比率“最小率”,随之,在对偶理论的基础上,又发现了约束条件的最小缩减率,或称约束最大放松规律。约束最小缩减率决定着经济运行过程中实际起着内在作用的那些约束条件的最优增长率,从而保证经济以正则状态来运行。
通俗地说,约束最小缩减规律就是在没有其它外来干预的情况下,经济自身的约束条件会客观地依据固定替代弹性所给定的比例,自动地确定自己最小的被替代水平,从而以最放松的水平,保证经济的正则运行。
从数值上来看,约束条件的最小被替代水平,就是最小的真替代减去最大的假替代所得到的差。
对于式(1.1),可以计算出约束条件vj的最小被替代率为:
rvk--约束条件 vk的数量增长率,k≠j,j,k=1,…,3.
一般地讲,给定观测到的增长率(rpi*,rvk*),式(1.8)的解是唯一的,并因此得到唯一的约束条件的缩减率Δrvj。这就是初始模型在基准状态上的解。数学对偶定理保证了这个解的存在性和唯一性,即在给定的基准点上得出:

依据上文的分析结果,特别是依据对偶定理可以得知,这里的 eβj,j=1,…,3,为第 j种约束条件的数量的最佳增长速率。而且,为便于理解,我们能够写出:

由这个公式右端项里各个因子的唯一性和已知性,或者说,由式(1.8)的结构可以得知,这个eβj是唯一的,并且是自我挑明的。也就是说,随着经济的增长,最优的固定数量的扩张速率是经济运行自身唯一给定的。因为经济运行遵循着固定替代弹性规律和资源利用的对偶规律,它的给定是自然的。
如果实际观测到的约束条件的增长率为eβj*,j=1,…,3,那么,其缩减率为 Δrvj*,且有 eβj*=Δrvj,若βj>βj*,也就是实际观测到的缩减率的增长率小于基准缩减率的增长率,最小约束限制将成比例地相应解除,部分资源属于过量被占用或投入,给经济带来一个扩张底数,而实际效率仍由固定替代弹性所规定,保持着内在的比例关系。此时,最小约束被解除的程度为eβj-βj*。这个被解除的程度就是实际的扩张速率。
对于式(1.7),可以理解为是由于技术进步和其它种种原因的作用,经济在总量水平上出现了变化。假定这种变化沿着一定的机制传导为下列数值,成为相应增长率的指数,即:

αi*--第 i种产品的价格增长率,i=1,…,3;
fpi(.)--第 i种产品的价格的传导函数,i=1,…,3.
同理,在约束条件方面,也存在类似的传导机制,导致:

βj*--第 j种约束条件的增长率,j=1,…,3;
fvj(.)--第 j种约束条件的传导函数,j=1,…,3.
容易证明,固定数量的增长,如同价格的增长和技术进步一样,可以明显地传递为相应变量或者约束条件的系数[9]。就此可以形成一定基础理论的形式化表达,进而,可以借用有关定理来进行深入的研究。
三、讨论与结论
约束条件的最小被替代率,意味着经济容量会自动地依据固定替代弹性所给定的比例调节出最小的限制程度,也就是给出经济发展的最适度的范围。如果市场是自由的,市场结构是自行调节出来的,例如就一个增长的经济来说,市场价格的增长率是自行调节的结果,那么,根据经济本身所具有的固定替代弹性和约束条件的自动最佳配置的规律,经济本身会沿着市场价格增长结构自行地进行调节,调节出经济发展的最适度的范围。这种增长是以基准状态为基线的,初始给定的约束条件,也就是出发点上的固定数量,会依据经济运行的最优化需要,不断缩减最小限制率,从而创造出经济容量,令经济不断扩展[10]。
依据自由市场自行调节的经济规律,对经济的直接干预通常会与约束条件有关。容易理解,在宏观干预里,金融干预通常是最为直接的,也是最为有效的。就我们现在所进行的这项研究来说,焦点可以聚集在货币数量的控制与通货膨胀的遏制上。
根据上述的约束最小替代规律和由固定替代弹性所决定的基准解,根据式(1.4)-(1.6)可以首先计算出式(1.1)中的固定替代弹性矩阵;然后根据式(1.8)计算出v3的最小被替代率为:

由式(1.1)给出的陈述可以知道,式(1.9)的结果便是货币固定数量的最小缩减率,是货币供给量的最小紧缩率,或者换一个角度说,也就是货币需求的最大宽松率。
显然,随着市场结构和固定数量的变化,在增长的经济里,价格、固定数量都会有所增长,导致货币投放数量也会有所增长。当然,这里所说的增长,是包括正的和负的两种增长情况在内的。设在t时刻,观测到价格的增长率为eαi*trpi*,固定数量增长率为 eβk*trvk
*,那么,货币的最佳增长率应该为 eβ3tΔrv3。为便于理解和计算,以式(1.9)为准,可以写出

eβ3t便是货币数量的最佳增长指数。根据上述分析,它也就是货币数量的最低紧缩指数。并由式(1.8)得知,决定它的最低紧缩速率是唯一的,是经济运行过程自然给定的。
另外,若令式(1.10)中的 t=0,便得出式(1.9)。 因而可以看出,式(1.10)所呈现的现象是以式(1.9)为本底的、在时间上的扩张。并且,就经济现象的观测而言,可以视式(1.10)为一般的表达,而式(1.9)是指定观测点上的结果。
由货币供给最小缩减率的定义可以知道,在增长的经济中,式(1.10)里的eβ3t为最低的紧缩指数。若实际观测到的货币供给量的缩减率低于它,那么,意味着现时的货币供给量的缩减率不及经济发展实际所需要的最小缩减率,也就是,货币供给量超出了经济发展实际所需要的最大宽松程度,投放的货币数量过多了,实物数量之间的比例被衡量其市场价值的尺度虚幻地放大了,那便实际上出现了通货膨胀。
设观测到的实际货币供给的指数为eβ3*t,且紧缩速率 β3*< β3,即出现了通货膨胀。对式(1.10)两侧同除 eβ3*t,得出:
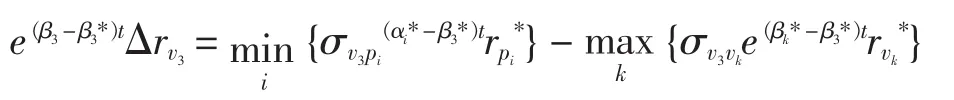
这里的 e(β3-β3*)t便是实际货币数量紧缩指数与最小约束紧缩指数的差,为增长速率的差距,是导致通货膨胀的重要因子;同时,我们也能看到,e(αi*-β3*)t和 e(βk*-β3*)t也不可忽视,是它们这 3 项(其中涉及4个因子)共同决定了通货膨胀的程度。因此,从遏制膨胀的角度来看,似乎就是下列的最优化选择,即:

这3个大于等于1的约束条件,体现了经济正则运行的要求。依据对数变换,可以将这个选择简化为:

这里,从可以进行干预的角度来看,只有βk*和β3*能够成为变量,即对膨胀进行遏制的切入点仅在于这两项。因为,“自由市场自行调节”决定了对市场价格的增长率αi*不应进行干预,仅能是给定的。而货币最小约束缩减率β3是基准值,更是给定的。

依据这个解所指示的,人们可以得出这样的概念:对于已经确定了的通货膨胀,遏制的切入点就是调节货币供给量的增长率和对货币用量具有最大促进弹性的这种需求数量的增长率。将货币数量投入的增长率调整至最小紧缩率,即β3*=β3;再将这种对货币用量具有最大促进替代弹性的需求数量的增长率调整到对货币用量具有最小替代弹性的产品价格的增长率,即βk*=αi*。这一选择过程的实现,或者说,可以对通货膨胀实施有效的遏制,依据经济学原理,只可是这样的结果。这个结果体现着宏观干预的作用,因为这个选择仅可在宏观水平上取得。另外,式(1.10)右端的两项内容,依据经济学原理可以认为,前一项,即的值可以完全由自由市场的力量来决定;而后一项,即则完全取决于市场外的宏观干预,因为这里的增长率完全是市场外生的。
值得注意的是,上述分析所依据的核心概念,或称有关通货膨胀的基本概念,就是货币约束的最小紧缩率,它的理论基础和内在的真实是经济世界实际存在的固定替代弹性规律。一切真实与规律都是看不见的,只有通过科学的抽象和推理才能把握它[11]。经济的真实和规律也是如此。
综合上文的全部内容可以看到,由于经济本底特性的真实存在,即固定替代弹性的规律的存在,导致经济的运行具有一致的和均匀的基本背景。任何具体的经济体,其内在的固定替代弹性都是给定的。因而,经济的运行,或者说自由市场自行调节的内容,是受着这个规律支配的,是有着固定特性可循的。在具体的运行过程中,会呈现出不同的结构和不同的格局,但其内在的决定均匀比例性的规律是不变的。经济科学发展到今天,人们已经发现了固定替代弹性这个规律,运用这个规律来解释和探索经济增长中出现的现象和问题,必定可以得到更加深入的认识,并得到更加精确的测度。上述的关于通货膨胀的分析即属于这方面的一个例子。
分析过程表明,对于具体的经济体而言,首先需要明确的便是它的固定替代弹性矩阵,也就是首先要计算出它的本底性的均匀不变的数值结构,由此出发,才可以确定基准的最小约束缩减率,自然也可以揭示不同生产和不同约束数量在确定最小约束缩减率中的地位。规律解释了现象,给定了真实的定义;科学指明了技术发展的方向。
模型(1.11)-(1.14)的结构表明,通货膨胀取决于 4 个因素,即 β3,αi*,βk*和 β3*。显然,当这里的αi*为消费品的价格增长率,且通货膨胀已经很明显时,它的效应可能会凸显出来。特别是如果这种消费品是农产品,在通货膨胀已经很明显的时候,如果把它用来作为膨胀的指示器,那应该是很简单、很明了的。似乎这便是CPI成为通货膨胀指示器的基本理由之一,似乎也是运用农产品价格增长率来回归通货膨胀指数这种经验做法的基本理由之一。可以认为,这些经验的摸索找对了方向,但不一定准确,更不够精确。人们已经习惯于用CPI指数作为通货膨胀的指示器,似乎从经验的角度表明了,在经济增长中,农业的增长对货币供给量的替代弹性是比较小的,因此,它的价格增长率的变化对货币基准用量的影响比较大。但这只是其中一个因素,从模型(1.11)-(1.14)的结构,以及由此所进行的上述分析结果可以看出,要准确分析通货膨胀的原因,还需要顾及另外那3个因素。因此,在经验运用中只注意到了CPI指数的作用,其实是不够精确的,仅是粗略的近似。而且,就引起通货膨胀的原因而言,它也未必是准确的。总之,似乎存在不少可以质疑的地方,需要得到实际验证。以往简单地围绕CPI测度所进行的数量分析,特别是以某种农产品价格增长率作为习惯变量所进行的数值计算和定量分析,应该有更坚实的经济学理论分析予以保证。有了这样的保证,相应的定量分析才会成为对经济理论的证明,而不仅仅成为统计学意义上的证明,更不是习惯臆想意义上的证明。
值得指出的是,迄今为止,对于通货膨胀的研究,在经济领域里,仍然是社会工作性的探索远远超过有关基础理论性的探索,而且,所运用的概念,来源于经验约定俗成的,更是远远超过由经济规律得以解释的[12,13]。 可喜的是,随着科技共同体的发展,某些基础理论的进展正在给经济学理论提供着新的启示。例如,天体物理学中的宇宙大爆炸理论,就曾经运用经济学中的有关通货暴涨的描述,来模拟宇宙本底的平直性,从而取得了重大的科学进展。反过来,借助基础科学的重大发现,运用其发现的重要规律,探索经济领域里类似通货膨胀这类的问题,也应该是可行的,而且也应该是可以取得明显进展的。
[1]Samuelson,P..Foundations of Economic Analysis [M].Cambridge,MA:Harvard University Press,1947:122-124.
[2]艾慧.中国当代通货膨胀理论研究[M].上海:上海财经大学出版社,2007.
[3]H.西蒙.社会科学与行为科学[M]//D.J.凯福尔斯 J.L.斯托尔乔,等.美国科学家论近代科技.范岱年,孟长麟,等,译.北京:科学普及出版社,1987:28.
[4]P.萨缪尔森 W.诺德豪斯.经济学[M].萧琛,译.北京:华夏出版社,1999:16-18.
[5]N.Gregory Mankiw.经济学原理[M].梁小民,译.北京:三联书店和北京大学出版社,1999:28-30.
[6]原宇,夏慧.金融学基础[M].北京:科学出版社,2010:72-75.
[7]孙中才.G函数与经济学的新进展[J].汕头大学学报:人文社会科学版,2006(6):20-24.
[8]孙中才.农业经济数理分析[M].北京:中国农业出版社,2006:114-123.
[9]Harrigan,J..Technology,Factor Supplies,and International Specialization:Estimating the Neoclassical Model[J].The AmericanEconomicReview1997,87(September):475-494.
[10]McFadden,D..Cost,Revenue,and Profit Functions,in:M.Fuss and D.McFadden(ed.),Production Economics:A Dual Approach to Theory and Applications,Volume 1,The Theory of Production[M].North-Holland Publishing Company:Amsterdam·New York·Oxford,1978:4-7.
[11]Einstein,A.,“Autobiographical Notes” in Albert Einstein,Philosopher-Scientist [C]//Schilpp,P.(ed),Open Court.Evanston,Ⅲ.,1949:17-18.
[12]F.Mishkin.The EconomicsofMoney,Banking,and Financial Market(Sixth Edition)[M].Pearson Addison-Wesley Press,2004:127-129.
[13]F.米什金.货币金融学[M].刘毅,蒋理,王秀萍,刘霞,夏乐,等,译.北京:中国人民大学出版社,2005:89-92.
Macro-intervention and Inflation
SUN Zhong-cai
(Department of Agricultural Economics,Renmin University of China,Beijing,100872)
Starting with the theoretical paradigm of the G function,the market economy model is constructed to reflect the concurrent operation of production and finance.Given the restraint to the corresponding fixed quantity in the sense of partial balance,the primary structure is obtained,in which the quantity of currency input or the level of currency supply is integrated.The primary structure can be used in the analysis of the quantity of currency employed in the economic operation.Based on the law of Constant Elasticity of substitution is computed the matrix of constant elasticity of substitution,which means the basic background of the economy running.Against the background,the changes in the structure of the economy and in its pattern are attributed to the cross effects between rate of growth in sector and the change in restraint.From this,the definition of inflation is given exactly by the difference between the growth rate of currency quantity observed in practical economy and the computed minimum reducing rate of restraint to currency quantity.Then the structure of this minimum reducing rate can be used to analyze the entry point of intervention at a macro level and the structure of the optimal behavior of the intervention.Finally,the measurements of macro-intervention are calculated.
running on the basic standard;Constant Elasticity of Substitution;inflation
F 123.16
A
1001-4225(2011)06-0060-06
2011-03-31
孙中才(1950-),男,辽宁辽阳人,经济学博士,中国人民大学农业经济系教授;兼任国务院第五届学位委员会学科评议组成员,美国纽约科学院(New York Academy of Sciences)院士。
佟群英)

