基于多源卫星测高数据的新一代全球平均海面高模型

金涛勇，李建成，姜卫平，王正涛

1.武汉大学测绘学院，湖北武汉430079；2.武汉大学地球空间环境与大地测量教育部重点实验室，湖北武汉430079

基于多源卫星测高数据的新一代全球平均海面高模型

金涛勇1，2，李建成1，2，姜卫平1，王正涛1，2

1.武汉大学测绘学院，湖北武汉430079；2.武汉大学地球空间环境与大地测量教育部重点实验室，湖北武汉430079

基于多源卫星测高数据，包括Geosat／GM、Geosat／ERM、ERS－1／168、ERS－2、Envisat－1、T／P和Jason－1数据，采用统一精密的模型或方法对各项地球物理改正和传播介质误差进行改进或重新计算，然后以T／P和Jason－1两种数据的共线平差作为参考基准，通过发展的全组合交叉点整体平差方法大幅度削弱了径向轨道误差和时变海面高影响。经比较后优选最小二乘配置格网化方法，以EGM2008高阶重力场模型由移去－恢复方法得到全球纬度－80°～82°范围内海域2′×2′平均海平面高模型WHU2009。与国际上较常用的CLS01平均海平面高模型及实测2年平均Jason－1比较表明WHU2009模型整体精度优于CLS01模型。

卫星测高；地球物理改正；交叉点平差；最小二乘配置；平均海面高

1 引 言

高精度高分辨率平均海面高模型是研究海洋动力环境变化的重要基础，在大地测量学和海道测量中的参考基准面均采用平均海面或与平均海面具有一定关系的参考面。卫星测高首次提供了直接测量全球海面高的技术，极大地提高了海洋观测数据的时空分辨率。自20世纪70年代成功获取第一颗测高卫星Geos－3观测数据以来，利用卫星测高观测数据先后建立了一系列全球和区域平均海平面高模型。早期，文献［1—4］利用Geos－3和Seasat数据计算得到了全球范围内精度为米级的平均海面高模型，其分辨率达到0.125°×0.125°。随后实施的Geosat／GM和ERS－1／168测高任务提供了海量海面高观测数据，T／P测高任务的观测精度有了厘米级水平新突破，由此相继出现了一系列接近厘米级精度的平均海面高模型，如OSU95MSS、GFZ MSS95A等［5－6］。在积累了海量的卫星测高观测数据和丰富的数据处理经验后，又发展了多源测高数据融合处理技术，推动了原有模型序列的升级换代，精度达到了厘米级水平，如GSFC00.1、CLS01、DNSC08等［7－9］，其中CLS01作为参考模型被广泛应用于最新一代测高卫星的数据处理中。我国在平均海面高模型研制领域也取得多项成果，建立了一系列中国海域平均海面高模型［10－12］。文献［13］建立的WHU2000是我国具有代表性的全球平均海面高模型之一，它利用7年的T／P卫星共线平均海面高作为参考基准，与ERS－1／168、ERS－2和Geosat／ERM数据进行联合交叉点平差得到，其精度水平与同时期的OSU MSS95和CLS＿SHOM98.2相当。

目前以卫星测高技术为主观测的海面高受多种误差影响，特别是系统性误差，基于该数据研制的平均海面高模型是含有误差的模型，有不同的精度水平。因此，建立高精度平均海面高模型首先要求采用的卫星测高数据有足够长的时间跨度以削弱更多的时变误差影响，例如至少20年。其次要求采用有效的数据处理方法，在研制的模型中平滑或消除各种短周期海平面变化的时变影响，如小波分解与重构的方法［14］。最后，更重要的是采用更严密精细的数据处理方法，最大限度地削弱或消除观测误差影响，例如精化各种系统性误差的改正模型。据此，本文采用了20.5年多源卫星测高数据，削弱时变影响和轨道误差的共线平差和全组合交叉点平差等数据处理方法，重点是对6种系统性误差精化改正模型，由此建立全球平均海面高模型WHU2009。

2 数据选取

针对各种卫星观测数据的精度和时间跨度，考虑海面时变信号的周年特性，本文所选取的数据如表1。为尽量削弱季节性海面时变信号，选取整周年的重复周期观测数据，而为提高海面高模型的分辨率，选取所有的非重复周期卫星观测数据。T／P卫星观测数据中只考虑精度较高的Topex测高仪观测数据。由于Jason－1作为T／P的后续卫星，两者具有相同的地面轨迹，本文采用全部的Topex数据，并补充Jason－1数据使两者总的时间跨度从1993年至2009年。

在所选数据中，重复周期观测数据Geosat／ERM、Topex、Topex／TDM、ERS－2、Jason－1和Envisat－1在赤道处的轨道间距分别约为164km、316km、316km、80km、316km和80km，其中Topex／TDM数据是T／P卫星轨道变换之后的观测数据，其轨道处于原T／P卫星轨道的中间，使其地面覆盖率增加一倍。而大地测量任务观测数据Geosat／GM和ERS－1／168在赤道处的轨道间距分别约为6km和8km，两者都是分别由两个观测时期组成，第二个观测时期的轨道经过调整后处于第一个观测时期轨道的中间，从而也使其地面覆盖率增加了一倍。由此可知，本文所选单星测高数据在赤道处的最小间距可达3km，而各种数据组合之后，可填充单星测高数据地面轨迹覆盖空白，大大地提高数据的空间采样率。因此，本文选择2′×2′作为平均海面高模型的有效空间分辨率，生成格网数值模型。

表1 本文全球平均海平面高模型建立中所采用的卫星观测数据Tab.1 Satellite measurements used in the establishing of global MSSH model

3 数据处理

3.1 数据预处理

卫星测高各种地球物理环境误差改正项对获得高精度海面高有很大影响，其改正精度直接影响到海面高的观测精度。近年来一些学者发现原始数据处理手册提供的相关改正模型存在问题，据此本文对现有同类改正模型作了深入分析对比，参阅国际最新处理方法和经验［15－23］，提出采用统一的精密改正模型及其算法，对所有的卫星测高数据地球物理环境误差改正作了改进或重新计算［24］。主要包括：① 对采用双频电离层改正的测高数据进行沿轨噪声平滑削弱影响，以Topex卫星为例比较得到平滑后相对平滑前差值均方差减小约6mm；对现常用的电离层改正模型，经与平滑后Topex双频电离层改正比较发现GIM实测模型精度最高，IRI2007模型精度优于其前期系列模型，故选择了IRI2007模型和GIM模型组合的方法对单频测高仪数据进行改正，即在GIM模型有效时选择该模型改正，否则选择IRI2007模型，同时比较发现Topex平滑双频测高仪存在约10mm的系统偏差，并在后续计算中进行了改正；② 针对现有海潮模型中已顾及大气潮汐分量S1和S2的情况，在与大气压相关的对流层干分量改正中进行扣除，避免重复改正，该项改正约达到±7mm；③对ERS－1、ERS－2、Envisat－1、T／P的对流层湿分量改正偏差进行校正，修复微波辐射计中个别频段漂移引起的误差，该项误差可使海面高产生约±1～2mm／a的偏差；④采用顾及大气正压高频信号的逆气压改正模型对所有测高数据进行重新改正，该项改正相对采用平均值为参考的逆气压改正时交叉点不符值均方差平均小约5.70mm，最大时达22.7mm；⑤利用最新的高精度GOT4.7海潮模型替换原有测高数据中改正模型；⑥ 对未采用严密非参数估计方法计算的ERS－1和ERS－2卫星海况偏差按该方法进行重新计算，该项改正使ERS－1和ERS－2数据相对原始改正的交叉点不符值方差减小了20～60cm2和1～5cm2。

除此之外，对ERS－1、ERS－2和Envisat－1测高卫星的仪器偏差和跟踪误差进行了改正［25－26］，其中，ERS－1和ERS－2的扫描点目标响应（SPTR）的距离改正误差分别达到－8～40mm和－60～7mm，超稳定振荡器（USO）的钟漂误差分别达到－11～25mm和－6～52mm，Envisat－1的USO误差在第40周期之前为20～30mm，而在第46周期后达到了5～6m。还将所有卫星的参考椭球转换到T／P卫星采用的参考椭球，有效地削弱了各卫星参考基准不一致误差，从而完成了多源卫星测高数据的精细预处理。

3.2 共线平差

对于建立分辨率低于2′×2′格网平均海平面高模型，可认为重复周期相同，地面轨迹同纬度观测值对格网点值的贡献大致相等。故对原有的共线平差法进行简化，避免正常点计算，选取参与共线的重复周期观测数据中稳定、观测状况好、数据多的轨迹作为参考轨迹，将其他重复周期观测数据内插到参考轨迹上，由此进行整体共线平差获得长时间平均海面高。计算中，对参考点和内插点间的海面高差再次进行限定以避免粗差，当大于0.5m时剔除。为保证平差后的数据至少能够消除一年内的时变影响，故当参与共线平差的观测值少于1年时，将该点位剔除。

共线法利用重复轨迹上同纬度点海面高的时间平均，可有效地消除周期短于所用共线轨迹时间跨度的时变海面高影响，和具有随机特性的时变量，共线平均海面可以认为至少在观测时间跨度内的稳态平均海面。T／P卫星和其后续卫星Jason－1被认为具有最高轨道精度和测量精度，在T／P卫星轨道改变之前，两者有相同的地面轨迹，其连续观测时间已有近16年，在如此长时间内获得的共线平均海面高与真实平均海面高应最接近，故将这两代T／P数据一起进行共线平差，其结果将作为以下交叉点平差中的参考基准。共线平差前后各数据的交叉点不符值比较如表2。

表2 重复周期观测数据共线平差前后交叉点不符值统计Tab.2 The crossover difference between before and after collinear adjustment of repeat cycle measurements m

3.3 多源卫星全组合交叉点平差

通过共线平差可以削弱重复周期观测数据的长波海面高变化，但残余径向轨道误差、海面时变短波信号和地球物理改正残差仍是平均海面高确定的主要影响。对长时间平均的海面高而言，所有测高卫星地面轨迹在交叉点处的平均海面高应该一致，据此可利用交叉点上轨道精度高的测高卫星观测数据改进轨道精度低的测高卫星观测值。交叉点平差就是将高精度卫星轨道作基准控制与其交叉的低精度卫星轨道，进一步消除上述残余误差，实现对后者观测值的改进。针对目前存在的多源卫星测高数据，本文对原有交叉点平差算法进行了扩展，使其能够同时整体平差9种测高数据。

交叉点平差中选择固定的高精度观测弧段数据解决秩亏问题。在本文采用的数据中，Topex和Jason－1测高卫星都具有很高的观测精度，两颗卫星组合的16年连续观测数据共线平差后交叉点不符值降低到2.2cm（表2），被选择作为交叉点平差中的固定观测值。轨道误差的高阶拟合多项式用于较小平差区域可得到较高的平差精度，但为避免轨道误差的过渡拟合，一般选择一阶多项式拟合大于100s的弧段，小于100s的弧段用常数偏差拟合［5］，在此原则下，进一步根据对平差精度的预估选取大小合适的平差区域。本文考虑大地测量任务测高数据存在的海面时变信号，认为较小的平差区域不仅能够削弱径向轨道误差，而且还能减小海面时变信号的影响。经比较并顾及计算效率，选取10°×90°作为区域平差范围，同时研究各平差区域之间的协调性和连续性问题，确定相邻纬度带平差区域应保持5°重叠，相邻经度方向平差区域保持45°重叠。

4 格网化方法比较

本文选择Shepard方法、连续曲率张力样条方法和最小二乘配置三种格网化方法进行比较择优。格网化过程中作了以下改进及参数的选择：

（1）考虑格网数据的密度分布及2′×2′的格网间距，Shepard方法拟合半径选取2倍格网间距，搜索半径内数据点个数不少于3个，当少于3个时，扩大拟合半径至满足条件为止。顾及数据的先验误差信息，将交叉点平差后单星交叉点不符值的作为对应数据噪声的方差引入到格网化过程中。

（2）因平均海面高是一个相对平滑的表面，连续曲率张力样条拟合内插方法的张力参数选择了0.25。该方法无法利用数据的先验误差信息，而交叉点平差后某些交叉点不符值可能较大，如果在格网化中采用相等的权，在其附近格网点的结果会产生较大波动［27］。由真实海面高观测值形成的交叉点不符值应为零，因此，本文首先将交叉点平差之后的交叉点不符值残差按卫星进行分配，使交叉点不符值为零，然后利用Akima样条插值，内插出相同轨道上其他观测点的改正值，改正后作为格网化的输入数据。

（3）最小二乘配置方法可有效利用观测值的先验信息解算内插值的最优统计估值。上面得到的超大规模海面高数据集使各格网点周围都分布了密集的观测值，此情况下最小二乘配置解对协方差函数的精确度已不敏感。本文采用Rene Forsberg于1987年编制GEOGRID程序，使用二阶Markov过程来描述协方差函数，由局部最小二乘配置法对离散数据进行格网化，减小计算工作量。Small证明了这种简化的协方差与严格确定的协方差用于大地水准面数据的格网化的结果几乎是一致的［28］。

最小二乘配置要求格网数据和推估信号具有零均值统计特性，故在格网化过程中，对三种方法都首先移去了EGM2008全球重力场模型计算的大地水准面，然后对残余海面高进行格网化，最后恢复大地水准面得到平均海面高模型。最小二乘配置格网化中还减去残余海面高的平均值使其严格满足零均值特性。下面选取纬度40°～50°，经度180°～200°范围作为试验区，对这三种方法进行了比较和分析。

图1～图3分别给出三种方法得到的格网化残差海面高。可以看出，都反映了较好的残差海面高整体变化特征，但前两种方法表现了较多的点位高频信息，呈现轨迹状条纹，而最小二乘配置结果非常平滑。为作进一步分析，选取全球平均海面高模型DNSC08和CLS01，以及两年共线平均的1～76周期实测Jason－1数据对三种方法恢复的平均海面高模型进行验证。其中，参与验证的Jason－1数据中的第1～第22周期数据在上述交叉点平差中未采用。

表3给出三种方法的数值比较结果，基于最小二乘配置格网化的平均海面高不论是与模型还是与实测Jason－1数据都吻合最好，说明其平滑作用并没有损失海面高高频信息。也就是说Shepard和连续曲率张力样条格网化结果存在沿轨迹高频抖动，造成这种问题的原因可能是沿轨迹海面高观测值存在相关性，而这两种方法都是格网化的解析法，不可能顾及沿轨数据相关性影响，且平噪功能低。而最小二乘配置法是基于观测值的协方差信息的统计推估方法，充分顾及利用了数据之间的统计相关性，且平噪功能高于解析法，因此更适合于对卫星测高沿轨观测数据的格网化。

表3 三种格网化平均海面高模型比较Tab.3 Comparison of the three gridded MSSH models m

5 模型建立与精度评定

基于上述比较结果，选取最小二乘配置方法用于格网化生成全球平均海面高模型。考虑到最小二乘配置计算速度问题，对测高数据全球覆盖范围（－80°～82°，0°～360°）进行分块处理，在－80°～60°，0°～360°范围内共分成126块20°×20°区域，60°～82°之间分成18块22°×20°区域。在全球共144块格网区域中，2个块区（40°～60°，60°～100°）处于亚洲大陆，1个块区（40°～60°，240°～260°）处于美洲大陆，均无观测数据。分块格网化之后对全球141块格网数据进行合并，对于重叠的经线和纬线以相邻两个块区的误差估值定权，进行加权平均，最终得到全球格网化残差平均海面高。

由于最小二乘配置同时具有内插和推估的功能，所以上述得到的141块格网残差平均海面高在每个格网点上都有数值，无法准确识别陆地和海洋界限。本文利用GMT生成了全球2′×2′陆地海洋界限数据，并联合上述合并的全球格网化残差平均海面高和全球EGM08大地水准面高生成了全球平均海面高模型WHU2009（图4），其中陆地上格网点值以EGM08大地水准面高补充，海洋和水域格网点值为残差平均海面高和EGM08大地水准面高之和。

图1 Shepard方法得到的格网残差海面高Fig.1 The gridded residual sea surface height by Shepard method

图2 连续曲率张力样条方法得到的格网残差海面高Fig.2 The gridded residual sea surface height by continuous curvature splines in tension

图3 最小二乘配置方法得到的格网残差海面高Fig.3 The gridded residual sea surface height by least square collocation method

图4 全球平均海面高模型WHU2009Fig.4 The global MSSH model WHU2009

下面采用格网化中相同的验证方法，联合WHU2000模型，对WHU2009模型进行了精度比较和分析。表4为－80°～82°范围内四个模型的差值统计，为避免粗差干扰，剔除了大于3倍标准差的模型差值。由于DNSC08模型采用近12年的T／P数据和大量其他卫星的重复周期数据，以及经过波形重跟踪处理的Geosat／GM和ERS－1／168两种大地测量任务数据，可以看出，其精度高于其他三个模型，而其他三个模型精度从高到低依次为WHU2009、CLS01、WHU2000。与WHU2000模型相比，WHU2009模型不仅精度有了提高，而且空间数据覆盖也更广泛。从所采用的数据来看，CLS01模型采用的Topex数据仅为7年，均少于WHU2009和DNSC08，因此精度较低。表5给出了四个模型与2年共线平均的Jason－1实测海面高在全球海域的比较结果，采用了纬度余弦定权。以Jason－1实测海面高为参考，各模型精度表现了与上述模型之间比较相同的结果。

6 结束语

本文利用统一精密的模型和方法对多源卫星测高数据地球物理环境误差改正进行了精化或重新计算，以T／P卫星轨道及其沿轨观测数据作为控制基准，通过共线平差和交叉点整体平差消除或大幅度削弱了径向轨道误差和时变海面高影响。Shepard、连续曲率张力样条和最小二乘配置三种格网化方法比较显示前两种方法格网化结果表现沿迹高频抖动，而最小二乘配置方法相对平滑，数值比较结果也表明该方法用于沿轨测高数据的格网化具有较高的精度。故选择该方法，以EGM08大地水准面模型作为参考场，由移去－恢复方法建立了全球海域－80°～82°范围内平均海面高模型WHU2009，与CLS01和DNSC08平均海面高模型以及实测2年平均Jason－1数据比较，验证了该模型的可靠性，结果表明该模型整体精度优于CLS01。

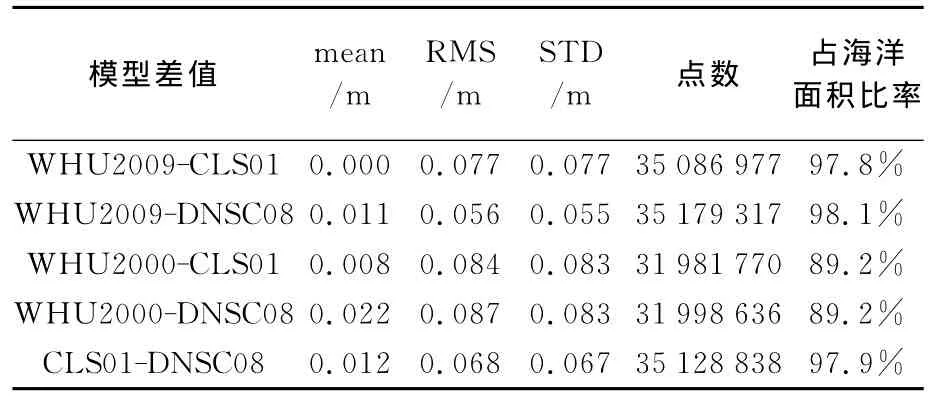
表4 剔除3倍标准差后全球平均海面高模型精度比较Tab.4 Comparison of global MSSH models after deleting 3 times’STD error

表5 全球海面高模型与2年平均Jason－1海面高比较Tab.5 Comparison of global MSSH models and 2－years’MSSH from Jason－1 m

［1］ RAPP R H.Mean Gravity Anomalies and Sea Surface Height Degradation from Geos－3Altimeter Data［R］.Columbus：Ohio State University，1977.

［2］ RAPP R H.Gravity Anomalies and Sea Surface Heights Derived from a Combined GEOS－3／Seasat Altimeter Data Set［J］.Journal of Geophysical Research，1986，91（4）：4867－4876.

［3］ MARSH J G，MARTIN T V，MCCARTHY J J.Global Mean Sea Surface Computation Using GEOS－3Altimeter Data［J］.Journal of Geophysical Research，1982，87（B13）：10955－10964.

［4］ MARSH J G，KOBLINSKY C J，ZWALLY H J，et al.A Global Mean Sea Surface Based Upon GEOS 3and Seasat Altimeter Data［J］.Journal of Geophysical Research，1992，97（B4）：4915－4921.

［5］ YI Y.Determination of Gridded Mean Sea Surface from TOPEX，ERS－1and Geosat Altimeter Data［R］.Columbus：Ohio State University，1995.

［6］ ANZENHOFER M，GRUBER T，RENTSCH M.Global High Resolution Mean Sea Surface Based on ERS－1 35and 168Day Cycles and Topex Data［EB／OL］.Postdam：GFZ，1995［2010－06－22］.http：∥adsc.gfz－potsdam.de／altimetry／mss／paper＿mss.html.

［7］ WANG Y M.GSFC00Mean Sea Surface，Gravity Anomaly，and Vertical Gravity Gradient from Satellite Altimeter Data［J］.Journal of Geophysical Research，2001，106（C12）：31167－31174.

［8］ HERNANDEZ F，SCHAEFFER P.The CLS01Mean Sea Surface：A Validation with the GSFC00.1Surface［EB／OL］.2001［2010－06－22］.http：∥www.aviso.oceanobs.com／fileadmin／documents／data／products／auxiliary／cls01＿valid＿mss.pdf.

［9］ ANDERSEN O B，KNUDSEN P.The DNSC08Global Mean Sea Surface and Bathymetry［R］.Vienna：EGU－2008，2008.

［10］ WANG Haiying，WANG Guangyun.Mean Sea Surface Determination From Geosat／ERM Altimeter Data in the China Sea and Its Vicinity［J］.Acta Geodaetica et Cartographica Sinica，1996，25（1）：25－30.（王海瑛，王广运.利用GEOSAT／ERM卫星测高数据计算中国近海海平面［J］.测绘学报，1996，25（1）：25－30.）

［11］ CHEN Junyong，LI Jiancheng，CHAO Dingbo.Determination of the Sea Level Height and Sea Surface Topography in the China Sea and Neighbour by T／P Altimeter Data［J］.Journal of Wuhan Technical University of Surveying and Mapping，1995，20（4）：321－326.（陈俊勇，李建成，晁定波.用T／P测高数据确定中国海域及其邻海的海面高及海面地形［J］.武汉测绘科技大学学报，1995，20（4）：321－326.）

［12］ LI Jiancheng，JIANG Weiping，ZHANG Lei.High Resolution Mean Sea Surface over China Sea Derived from Multi－satellite Altimeter Data［J］.Geomatics and Information Science of Wuhan University，2001，26（1）：40－45.（李建成，姜卫平，章磊.联合多种测高数据建立高分辨率中国海平均海面高模型［J］.武汉大学学报：信息科学版， 2001，26（1）：40－45.）

［13］ JIANG Weiping，LI Jiancheng，WANG Zhengtao.Determination of Global Mean Sea Surface WHU2000Using Multi－satellite Altimetric Data［J］.China Science Bulletin，2002，47（19）：1664－1668.

［14］ ZHANG Chuanyin，WEN Hanjiang.Fine Characteristics of Along－track Sea Surface Heights and Preliminarily Study of Its Applications［J］.Acta Geodaetica et Cartographica Sinica，2002，31（2）：112－117.（章传银，文汉江.卫星测高沿轨海面高的精细结构及其应用技术初探［J］.测绘学报，2002，31（2）：112－117.）

［15］ IMEL D.Evaluation of the TOPEX／POSEIDON Dualfrequency Ionosphere Correction［J］.Journal of Geophysical Research，1994，99（C12）：24895－24906.

［16］ BILITZA D，REINISCH B.International Reference Ionosphere 2007：Improvements and New Parameters［J］.Advances in Space Research，2008，42（4）：599－609.

［17］ RAY R，EGBERT G.The Global S1Tide［J］.Journal of Physical Oceanography，2004，34（8）：1922－1935.

［18］ RAY R.Comparisons of Global Analyses and Station Observations of the S2Barometric Tide［J］.Journal of Atmospheric and Solar－terrestrial Physics，2001，63（10）：1085－1097.

［19］ SCHARROO R，LILLIBRIDGE J，SMITH W，et al.Cross－calibration and Long－term Monitoring of the Microwave Radiometers of ERS，TOPEX，GFO，Jason，and Envisat［J］.Marine Geodesy，2004，27（1－2）：279－297.

［20］ CARRÈRE L，LYARD F.Modeling the Barotropic Response of the Global Ocean to Atmospheric Wind and Pressure Forcing：Comparisons with Observations［J］.Geophys Res Lett，2003，30（6）：1275－1578..

［21］ JIN Taoyong，LI Jiancheng，WANG Zhengtao，et al.The Inverse Barometer Correction in Satellite Altimetry and Its Effect on Mean Sea Level Change［J］.Geomatics and Information Science of Wuhan University，2010，35（9）：1017－1020.（金涛勇，李建成，王正涛，等.卫星测高逆气压改正及其对海平面变化的影响［J］.武汉大学学报：信息科学版，2010，35（9）：1017－1020.）

［22］ RAY R D，LYARD F，ROBLOU L.Thoughts on Shallow－water Tides ＆Altimetry［R］.Silver Spring：CIOSS／NOAA Coastal Altimeter Workshop，2008.

［23］ GASPAR P，LABROUE S，OGOR F，et al.Improving Nonparametric Estimates of the Sea State Bias in Radar Altimeter Measurements of Sea Level［J］.Journal of Atmospheric and Oceanic Technology，2002，19（10）：1690－1707.

［24］ JIN Taoyong.Research on Global Mean Sea Level and Its Change from Multi－oceanic Observations［D］.Wuhan：Wuhan University，2010.（金涛勇.多源海洋观测数据确定全球海平面及其变化的研究［D］.武汉：武汉大学，2010.）

［25］ MARTINI A，FÉMÉNIAS P.The ERS SPTR2000Altimetric Range Correction：Results ＆Validation［R］.Frascati：ESA／ESRIN，2000.

［26］ FAUGÈRE Y，OLLIVIER A.Design and Assessment of a Method to Correct the Envisat RA－2USO Anomaly［R］.Frascati：ESA，2006.

［27］ OLGIATI A，BALMINO G，SARRAILH M，et al.Gravity Anomalies from Satellite Altimetry：Comparison between Computation via Geoid Heights and via Deflections of the Vertical［J］.Journal of Geodesy，1995，69（4）：252－260.

［28］ SMALL H.A Comparison of Techniques for the Gridding of Satellite Altimeter Data［R］.Columbus：Ohio State University，1992.

The New Generation of Global Mean Sea Surface Height Model Based on Multi－altimetric Data

JIN Taoyong1，2，LI Jiancheng1，2，JIANG Weiping1，WANG Zhengtao1，2
1.School of Geodesy and Geomatics，Wuhan University，Wuhan 430079，China；2.Key Laboratory of Geospace Environment and Geodesy，Ministry of Education，Wuhan University，Wuhan 430079，China

Based on multi－satellite altimetric data，including Geosat／GM、Geosat／ERM、ERS－1／168、ERS－2、Envisat－1、T／P and Jason－1，it is improved and re－computed their geophysical corrections by unified accurate models and methods.Then，by assuming the dataset combing the T／P and Jason－1 measurements which are collinear adjusted as reference，the radial orbit error and time－variation affect of sea surface height are reduced through the developed whole combination crossover adjustment.Furthermore，global MSSH model named WHU2009 with the boundary from－80°to82°and resolution of 2′×2′is achieved by remove－restore method and least square collocation grid method with EGM2008 high degree gravitation model.Compared with CLS01 model that commonly used internationally and the dataset that collinear adjusted with 2 year Jason－1 measurements，it is concluded that WHU2009 has better integrated accuracy than CLS01.

satellite altimetry；geophysical correction；crossover adjustment；least square collation；mean sea surface height

JIN Taoyong（1982－），male，PhD，lecturer，majors in satellite geodesy.

1001－1595（2011）06－0723－07

P228

A

国家863计划（2009AA121402）；国家自然科学重点基金（406374034）；教育部新世纪优秀人才计划（NCET－07－0633）；地球物理大地测量国家测绘局重点实验室开放基金（10－02－08）

丛树平）

2010－12－06

2011－05－15

金涛勇（1982－），男，博士，讲师，研究方向为卫星大地测量学。

E－mail：tyjin＠sgg.whu.edu.cn