一种用于无线传感器网络节点递增式定位的新方法*

熊伟丽，唐蒙娜，徐保国

(江南大学轻工过程先进控制教育部重点实验室，江苏无锡214122)

无线传感器网络技术作为一种新的信息获取和处理技术，具备传统技术不可比拟的优势，在军事和民用领域拥有广阔的应用前景。正确的节点定位是无线传感器网络构建和维护、监测定位、目标跟踪等功能实现的前提和基础［1］。目前用的较多的节点定位方法是最小二乘法、加权最小二乘法等，然而最小二乘法虽然考虑了参考节点的定位误差，但没有考虑到递增式定位方法中不同级的参考节点定位误差的不同［4－5］;加权最小二乘法虽然考虑了各级参考节点的定位误差的不同，但其权值的确定不能使节点定位达到最优。

本文延续递增式模型中不同级参考节点定位误差不同的特点，针对加权最小二乘法中权值选取的不足，提出最优加权最小二乘法对该问题进行改进，在估计误差方差矩阵最小时取得最优权值，最终得到最优估计解。该方法能使节点的估计坐标与真实坐标间的误差保持在一个较稳定状态，同时也使误差减小，确保后级节点定位的准确性，尽量减小递增误差带来的影响。仿真结果表明，最优加权最小二乘在递增式节点定位中具有明显的优越性。

1 递增式定位与累积误差的形成

按照节点定位的先后次序不同，定位方法可分为递增式定位法与并发式定位法。并发式定位法中所有节点同时进行位置计算，要求锚节点通信范围较大，适用于小型传感器网络。当网络中节点较多、覆盖范围较广时采用递增式定位法较为合理［6－7］。为了降低成本，应减小WSN中锚节点所占的比例，但同时也降低了定位节点覆盖率。为了提高定位节点的覆盖率，将已定位节点升级为参考节点，利用参考节点迭代定位将定位节点的范围逐步扩展到整个网络，这就是递增式定位法［8］。锚节点为能够通过GPS直接定位的节点。

递增式定位法引入了误差累积的问题，参考节点本身可能存在较大的位置误差，由于测距误差和参考节点位置误差同时作用，在下一轮的定位估计中引入了更大的误差，当网络规模较大时，误差累积造成的位置误差将不容忽视［2，9－10］。递增式定位方法中，被定义为同一级节点的定位是同时进行的。假设目标节点与定位节点之间的距离已获得，且测距误差与距离有关，建立一个模拟无线传感器网络来对递增式定位中的累积误差进行分析［3，11］。图 1 中，假设 S1、S2、S3为锚节点，节点A～E为待定位的未知节点。连线表示在通信范围内的节点，图中线段长度不代表距离。设锚节点为零级节点，一级节点是指只由锚节点直接定位的节点A;只由一级节点定位或由锚节点和一级节点共同定位的节点C称为二级节点;以此类推，B、D为三级节点，E为四级节点。假设锚节点定位无误差，由前面提到的递增模式可知，后级节点的定位误差通常都大于其前级节点，节点定位误差随着定位的逐级进行呈现增大的趋势。因此，各节点误差大小关系为:S1、S2、S3＜A ＜C ＜B、D ＜E。为了解决误差累积问题，引入最优加权最小二乘估计的方法，在最小二乘估计中加入最优权值，使定位误差方差达到最小，提高定位精度。

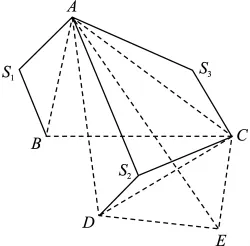
图1 网络中的节点

2 最优加权最小二乘的节点定位方法

改进的最优加权最小二乘法相对于其他普通的加权最小二乘，不仅考虑了不同级节点误差因子的差异，并在估计误差的方差矩阵E［(－H)(－H)T］达到最小时取得权值，能使为真值H的最优估计。下面分别对一级节点、二级及二级以上节点的定位进行分析。

2．1 一级节点定位

在本段中，对无线传感器节点定位算法进行建模，列出方程，针对传统的加权最小二乘法存在的估计有偏问题，列出使估计最优的两个条件，引入最优加权最小二乘法，不仅得出对节点位置的最优估计，且此最优估计无偏。

在实际无线传感器网络中，各级节点都可能有无数个。假设网络中零级节点坐标为Si(Xsi，Ysi)，且不存在位置误差，一级节点坐标为A(XA，YA)，测得待定位节点A到各零级节点的距离为dsi，其中测距误差εi1与节点间距离成比例，独立且服从方差为高斯分布，则可建立如下方程组:

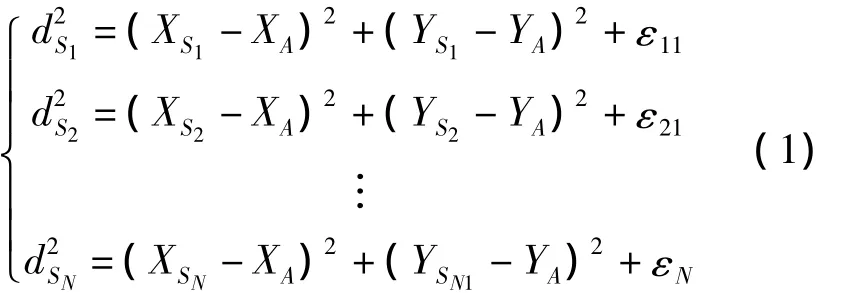
从方程组(1)的第一个方程开始分别减去最后一个方程，所得的方程组表示为矩阵形式:

式中:

本文针对上述问题提出最优加权最小二乘法，其核心是找到最优的权系数阵W，使其估计误差的方差矩阵达到最小，并且为无偏估计。推导如下:

估计误差为:

式中:Kij是相关系数，由于各测距误差不相关，当i≠j时，Kij=0。

在一级节点的定位中，权值取值的不同主要取决于测距误差的不同。上面计算的权值是在方程作差的基础上取得的。因此，要了解各参考节点的权值，需再组建一个简单方程组，经过计算得到各节点的权值，且各权值略小于1。

2．2 二级及二级以上节点定位

由于无线传感器节点间存在距离测量误差，造成一级节点的定位有误差，而这些存在误差的节点将被后一级节点作为参考节点来对自身进行定位。由于参考节点受本身的定位误差和距离测量误差的影响，后一级节点的定位误差呈现增大的趋势。要提高节点的定位精度，除了提高距离测量精度外，还需减小参考节点定位误差的影响。

如图1所示C为二级节点，其参考节点包括两个零级参考节点和一个一级节点。由于一级节点受距离测量误差影响，其估计位置必然存在误差，因此一级节点的定位误差大于零级参考节点的定位误差，根据不同节点对C节点精确定位的影响大小，赋予不同的权值。

对于二级及二级以上的节点，其参考节点存在不同程度的定位误差，设各参考节点定位误差εi2符服从高斯分布，设其均值为零，方差为σ2il。由于测距误差εi1也服从高斯分布，因此εi1+εi2仍服从高斯分布，方程组可表示为:

在定位级数为二级以及二级以上的待定位节点时，由于参考节点可能是不同级的，而各级的定位精度不同，赋予的权值也各不同，甚至有较大差异。参考节点中，除了锚节点权值略小于1，而对于其它节点，由于存在节点位置本身的定位误差，其权值都小于1，且级数越高，其本身误差越大，越不利于后级节点的正确定位，对应的权值也越小。

3 误差分析

当只存在测距误差，各级参考节点的定位误差没有显著差别，即测距误差对各级节点的影响大致相同;当只存在参考节点定位误差时，后级节点的定位误差明显大于前级节点。在递增式定位过程中，各级节点定位误差来源于测距误差与参考节点的定位误差，因此存在严重的累积误差，在相同测距误差的情况下，累积误差主要是由节点的定位误差决定的，如图2所示。

图2 三种情况下的定位误差对比图

每条路径的测距误差与其路径长度有关，路径最短的测距误差服从独立的高斯分布 N(0，σ2)。假设待定节点共K个，第i个待定位节点的真实坐标为(Xi，Yi)，而根据本文所运用的定位算法得到的定位坐标为(i，i)，i=0，1，2，…，K。定义节点定位误差为节点的真实位置与估计位置间的距离与通信距离D之比各级节点平均定位误差为同级节点定位误差之和除以节点数。

本文利用的最优加权最小二乘可以尽量减小累积误差带来的问题，通过计算给不同级节点引入了不同的权值，误差越大的节点对正确定位越不利，相应的权值就越小，并赋予了结果对误差方差最优的特点。下一节对改进方法进行仿真分析与对比。

4 仿真与对比

以100 m×100 m的正方形农田为单位部署100个节点，将节点射频通信距离设为15 m，测距精度使用相对误差表示，即误差占射频通信距离的比例，测距误差服从高斯分布。部署于农田中的无线传感器节点的主要功能是采集节点周围的土壤信息，如温度、湿度及土壤紧实度等。

仿真阶段必须选择出合理的权值，使定位误差达到最小。加权最小二乘法中，为了取得能使定位误差达到相对小的权值，需多次取值进行结果对比。最优加权最小二乘法较加权二乘法的最大优势是权值能根据方差阵的逆阵来取得最高精度的估计值，结果同样遵循级数越高，权值越小的原则。测距误差增大时，要达到最小定位误差，权值有相应的减小，但这种减小的趋势不明显，即测距误差的影响不占主导作用，影响主要是由参考节点的位置误差造成的。图3为参考节点定位误差ε的方差取不同值时的平均误差图。

图3 ε方差不同时各级节点平均定位误差对比图

由图3可知，ε取不同值时，各级节点平均定位误差各不同。ε的方差越大，节点平均定位误差也越大。在测距误差为1%时，由于测距误差在距离的±1%间呈正态分布，因此其节点位置误差也有变化。图4是ε的方差一定时，应用最小二乘法、加权最小二乘法和最优加权最小二乘法所得到的待定位节点误差的对比图。

图4 测量误差一定时不同算法的误差对比图

从图4中的对比可以看出，应用最优加权最小二乘法得到的定位误差明显低于最小二乘法和加权最小二乘法，对节点的正确定位具有有效的改进作用。另外由图可知，不管用何种方法，同一点处的定位误差呈现相同的趋势，即低级节点的定位误差小于高级节点，也验证了本文方法的正确性。

5 结束语

本文根据递增式定位方法的特点，提出最优加权最小二乘的方法来改进递增式节点定位中的缺陷，通过不同测距误差下定位误差大小的对比，在一个相对最小的测距误差下，运用最优加权最小二乘法与运用其他定位方法进行MATLAB仿真对比。从仿真结果可以看出，该方法能有效抑制无线传感器定位迭代循环过程中误差累积的影响，使递增式节点定位方法能够越来越广泛的应用于无线传感器网络的定位中。

［1］ 曹晓梅，俞波．传感器网络节点定位系统安全性研究［J］．软件学报，2008，9(4):869 －877．

［2］ 王建刚，王福豹，段渭军．加权最小二乘估计在无线传感器网络定位中的应用［J］．计算机应用研究，2006，(9):41 －42．

［3］ 嵇玮玮，刘中．递增式传感器节点定位方法的累积误差分析及其改进［J］．南京理工大学学报，2008，32(4):496 －501．

［4］ 范伟军，周必方，夏良正等．基于最小二乘法准则的光学综合孔径观测目标傅里叶信息提取［J］．光子学报，2004，33(4):72－475．

［5］ 包志华，周晖，邵世煌．基于智能估计的无线传感器网络定位算法［J］．传感技术学报，2008，21(10):1755 －1769．

［6］ Hwang S，Willians D B．A Constrained Total Least Square Approach for Sensor Position Calibration and Direction Finding［C］//Proc of the IEEE National Radar Conference．USA，1994:155 －159．

［7］ Huang Z，Lu J．Total Least Square and Equilibration Algorithm for Range Difference Location［J］．Electronics Letter，2004，40(5):121 －122．

［8］ Savvides A，Han C C，Srivastava M B．Dynamic Fine-Grained Localization in Ad-Hoc Networks of Sensors［C］//Proc of 7th Annual International Conf on Mobile Computing and Networking(MobiCom)．USA，2001:166－179．

［9］ 魏叶华，李仁发，罗娟，等．基于支持向量回归的无线传感网络定位算法［J］．通信学报，2009，30(10):44 －50．

［10］黄浩，卢文科．无线传感器网络中基于锚节点反馈的多跳测距定位算法改进［J］．传感技术学报，2009，22(2):269 －272．

［11］ C K Chui，G Chen．Kalman Filtering with Real-Time Applications［M］．Springer-Verlag，1987．

［12］ CostaJ A，Patwari N，Hero A O．Distributed Weighted Multidimensional Scaling for Node Localization in Sensor Networks［J］．ACM Transactions on Sensor Networks，2006，2(1):1 －26．

［13］ Niculescu D，Nath B．DV Based Positioning in Ad Hoc Networks［J］．Telecommunication systems-Modeling，Analysis，Design and Management，2003，22(1/4):267 －280．