基于SVR的多传感器数据融合处理方法*
丁 蕾,廖同庆,陶 亮*(.安庆师范学院物理与电气工程学院,安徽安庆4633;).安徽大学计算智能与信号处理教育部重点实验室,合肥30039
在实际的测量系统中,大多数传感器都存在交叉灵敏度,表现在传感器的输出不仅决定于其目标参量,还受其它参量的影响。存在交叉灵敏度的传感器,其性能不稳定,测量精度低。多传感器数据融合技术就是通过对多个参数的监测并采用一定的信息处理方法达到提高每一个参量测量精度的目的,为开发多功能传感器系统开辟了途径。[1]
传统的多传感器数据融合处理方法主要有两种:①多维回归分析法[2-4],它由多维回归方程来建立被测目标参量与传感器输出量之间的关系,然后按最小二乘法原理来计算回归方程中的系数,但该方法需要求解较大规模的矩阵方程。②人工神经网络方法[5-7],它不需要建立复杂的函数解析式,具有很强的非线性逼近能力,但存在过拟合现象,泛化能力较差。而支持向量机是Vapnik及其研究小组在统计学习理论的基础上提出来的一类新型的机器学习方法[8],用于回归估计的支持向量机方法(support vector machine for regression,即SVR)以可控制的精度逼近非线性函数,具有全局最优、良好的泛化能力等优越性能。因此将SVR方法引入到多传感器数据融合处理中。实验表明该方法降低了交叉灵敏度,提高了传感器的测量精度,而且处理速度快,是一种行之有效的多传感器数据融合处理方法。
1 用于回归估计的SVR算法
基于结构风险最小化准则构造的支持向量机(SVM)方法,最早是针对模式识别问题提出的,Vapnik引入ε不敏感损失函数,将其推广到回归估计中并且表现出很好的学习效果。下面简要介绍一下用于回归估计的SVR标准算法[9]。
假设给定了训练数据{(xi,yi)i=1,2,…,l},其中是第i个学习样本的输入值,且为一d维列向量,yi∈R 为对应的目标值。
先定义ε不敏感损失函数为

即如果目标值和经过学习构造的回归估计函数的值之间的差别小于ε,则损失等于0。
支持向量机通过定义适当的核函数K(xi,xj)将输入样本空间非线性变换到另一个特征空间,然后在这个特征空间中构建回归估计函数,其中K(xi,xj)=φ(xi)·φ(xj)为某一非线性函数。
假设非线性情形下的回归估计函数为:

目标是寻找ω、b对,使在(1)式固定的条件下最小化置信范围。考虑到约束条件不可实现时引入松弛变量,这样最优化问题为
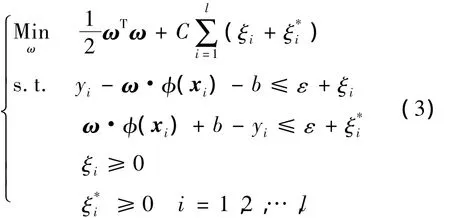
利用拉格朗日乘子法求解(3)式,并根据最优化理论得到(3)式的对偶最优化问题为:


其中

上式中NNSV为标准支持向量数量。
2 压力传感器数据融合处理方案
众所周知的压阻式压力传感器存在对静压、温度的交叉灵敏度,尤其是它对温度的敏感成为它的最大缺点。硅压阻式压力传感器作为一个两功能传感器可测量两个目标参量,目标参量压力p的输出值为电压U,目标参量温度t的输出值为电压Ut。这两个测量值不仅是其目标参量的函数,还受到另外一个环境参量(工作温度t或所受压力p)的影响,为此可构造两个二元函数 U=f1(p,t)和 Ut=f2(p,t)来反映传感器的两个输出量,两者之间相互存在交叉灵敏度。
考虑到当工作温度t一定时,U和Ut只是压力p的一元函数U=f3(p)和Ut=f4(p),此时可以利用SVR模型对两个输出电压进行融合处理,为此构造一个形如(2)式的回归估计函数p=g1(U,Ut),反映目标参量p与这两个测量电压值之间的关系。此时(2)式中的,它作为学习样本的输入值是一个2维列向量,实验中的标定压力即为对应的目标值。依据SVR理论,用构造的回归估计函数g1(x)去逼近标定压力的问题转化为形如(3)式的约束最优化问题,求解这个问题就可得出形如(5)式的回归估计函数g1(U,Ut)。用这个函数建立的模型可以提高目标参量p的测量精度,减小交叉灵敏度。同理,我们也可以构造一个函数t=g2(U,Ut),反映所受压力p一定时,目标参量t与这两个电压值之间的关系,从而提高它的测量精度。基于SVR的压力传感器数据融合系统框图如图1所示。

图1 SVR数据融合模型
3 仿真实验与分析
文献1利用JCY-101型压力传感器进行了二维标定实验,它选取了6个压力标定点和5个温度标定点,实验数据如表1所示。其温度灵敏度系数αs和压力灵敏度系数αp分别定义为:

式中t2、t1为工作温度的上、下限值;p21为压力输入的上、下限值;U(t2)、U(t1)为同一输入压力下,工作温度分别为 t2、t1时压力传感器的输出;Ut(p2)、Ut(p1)为同一温度下,输入压力分别为p2、p1时温度传感器的输出。

表1 二维实验标定数据
由实验标定数据可计算出工作温度在28℃到70 ℃范围内,p=0 kPa时,αs=1.02 ×10-2/℃;p=40 kPa时,αs=1.76 ×10-3/℃;输入压力在 0 kPa到50 kPa范围内,t=28 ℃ 时,αp=7.26 ×10-2/50 kPa;t=70 ℃时,αp=6.58 ×10-2/50 kPa。
利用SVR模型对表一中的实验数据进行数据融合处理,可分别计算出输出压力值和输出温度值,它们与压力标定值和温度标定值的比较列在表2、表3中。此时传感器的灵敏度系数也可采用下式来表示:

式中ΔT为工作温度的变化范围;Y(FS)为传感器的量程;Δym为当温度变化ΔT时,全量程范围内某一输入量漂移的最大值。
当Δym表示温度变化ΔT时零位值的最大改变量时,αs表示零位温度系数 α0,减小 α0的数值,提高零位值相对温度变化的稳定性对于降低温度附加误差,校正零点漂移是非常必要的[10]。
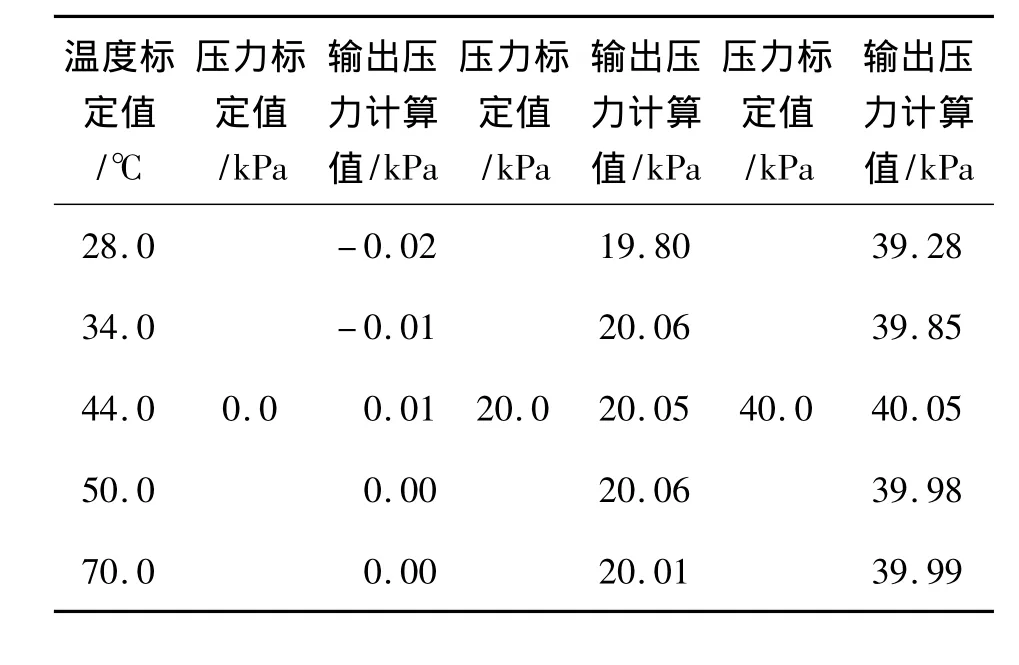
表2 SVR方法计算的压力值与压力标定值
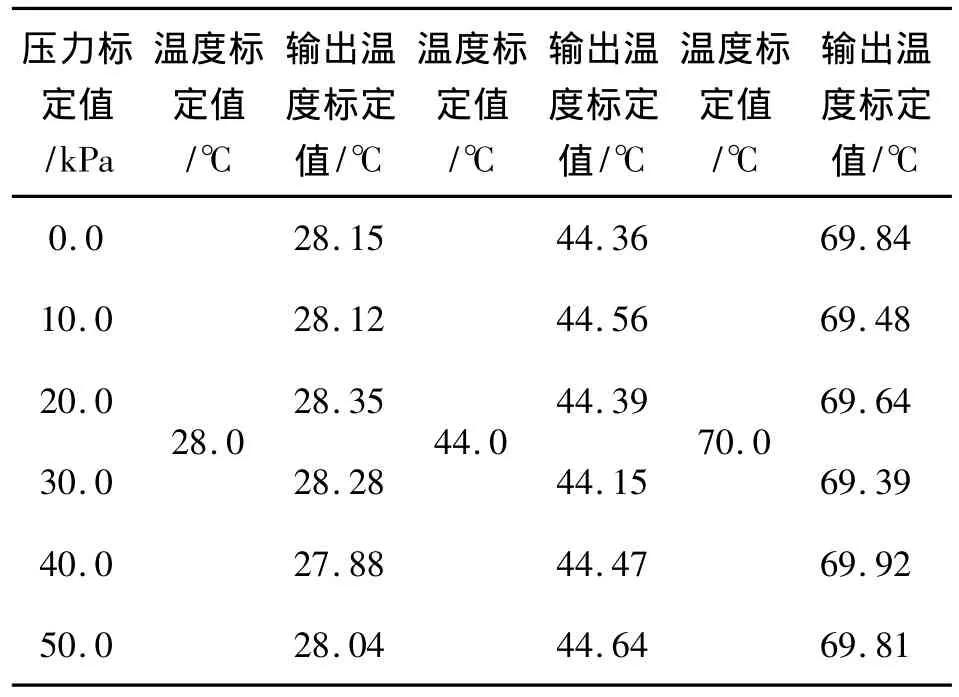
表3 SVR方法计算的温度值与温度标定值
由(8)式可计算出工作温度在28℃到70℃的范围内变化时,零位变化0.03 kPa,其等效零位温度灵敏度系数为1.43×10-5/℃;p=40 kPa时,漂移最大值为0.23 kPa,其等效温度灵敏度系数为1.09×10-4/℃。输入压力在0 kPa到50 kPa范围内,t=28℃时漂移最大值为0.47℃,其等效压力灵敏度系数为1.12×10-2/50 kPa;t=70℃时漂移最大值为0.61℃,其等效压力灵敏度系数为1.45×10-2/50 kPa。可见进行数据融合处理后的灵敏度系数均降低1~2个数量级,也就是说传感器的稳定性提高了1~2个数量级。
将这个计算结果与文献1和3中的多维回归分析法和神经网络方法比较,会发现SVR方法达到了上述方法的处理效果;而且等效零位温度灵敏度系数α0降低了3个数量级,这个结果比文献1中的α0=4.9 × 10-5/℃,文献[11]中的 α0=3.5 ×10-4/℃下降得更多,零位压力相对温度变化的稳定性明显优于上述两种传统的数据融合处理方法。
另外标准SVR算法的速度不快,这会影响该方法的实时处理,若在本实验中采用LSVM-R算法[12]进行融合处理,可在保持相同精度的前提下将速度提高56.8%。
以上实验均利用 matlab6.5编程,运行于Core2/2G,2G 内存PC。
4 结束语
将用于回归估计的支持向量机(SVR)方法引入到多传感器数据融合处理中,对两功能的硅压阻式压力传感器的目标参量压力和温度进行数据融合处理,可以降低交叉灵敏度系数,提高测量精度和稳定性。而且,这种新方法融合处理后的零位压力相对温度变化的稳定性明显优于传统的数据融合处理方法。
[1] 刘君华.智能传感器系统[M].西安:西安电子科技大学出版社,1999.264 -265.
[2] 黄永武,王伟平,王晓书.基于数据融合的压力传感器温度误差补偿方法[J].仪表技术,2008(4):65-67.
[3] 张艳锋,严家明.基于最小二乘法的压力传感器温度补偿算法[J].计算机测量与控制,2007,15(12):1870 -1871.
[4] 赵秋,孙思梅,孙以材.信息融合在压力传感器中的实现[J].传感技术学报,2006,19(4):1268 -1271.
[5] 张银慧,何平,李晓峰,等.基于径向基神经网络的压力传感器信息融合技术[J].河北工业大学学报,2008,37(1):22 -26.
[6] 张耀锋,孙以材,刑晓辉.基于人工神经网络的压力传感器的温度补偿[J].电子学报,2008,36(2):358 -361.
[7] 高美静,赵勇,谈爱玲.基于遗传小波神经网络的多传感器信息融合技术的研究[J].仪器仪表学报,2007,28(11):2103-2107.
[8] Vapnik V N.Statistical Learning Theory[M].New York:Simon Haykin,1998:91 -101.
[9] 杜树新,吴铁军.用于回归估计的支持向量机方法[J].系统仿真学报,2003,15(11):1580 -1585.
[10]苏亚,孙以材,李国玉.压力传感器热零点漂移补偿各种计算方法的比较[J].传感技术学报,2004,17(3):375 -378.
[11]田立强,孙以材,赵彦晓.两种多传感器信息融合方法的比较[J].传感器世界,2002,8(11):9 -13.
[12]丁蕾,陶亮.改进的用于回归估计的支持向量机学习算法[J].计算机工程与应用,2005,41(19):44 -46.

