The Factorization Method to Solve a Class of Inverse Potential Scattering Problems forSchrdinger Equations∗

LI YUANAND MA FU-MING

(1.School of Mathematics,Jilin University,Changchun,130012)

(2.School of Mathematics,Heilongjiang University,Harbin,150080)

The Factorization Method to Solve a Class of Inverse Potential Scattering Problems for
Schrdinger Equations∗

LI YUAN1,2AND MA FU-MING

(1.School of Mathematics,Jilin University,Changchun,130012)

(2.School of Mathematics,Heilongjiang University,Harbin,150080)

This paper is concerned with the inverse scattering problems for Schrdinger equations with compactly supported potentials.For purpose of reconstructing the support of the potential, we derive a factorization of the scattering amplitude operatorAand prove that the ranges of (A∗A)1/4andGwhich maps more general incident fields than plane waves into the scattering amplitude coincide.As an application we characterize the support of the potential using only the spectral data of the operatorA.

factorization method,inverse scattering,Schrdinger equation,interior transmission problem

1 Introduction

Inverse scattering problem for Schrdinger equation is an important class of problems in mathematical physics.It’s more difficult and challenging than the case of Helmholtz equation for the complexity brought by the potential term.One way of stating this problem is to reconstruct the potential or at least its support given the scattering amplitude data.For one-dimensional and radial Schrdinger equations,the inverse scattering problems are fairly well understood(at least for certain classes of potentials)(see[1]).In higer dimensions, however,there are still many open problems,and the methods developed are also far from being complete.Some tipical methods developed in multidimensional inverse scattering problems can be found in[2]–[5].A uniqueness theorem and some inversion formulas with both exact and noisy data and the stability results for the three-dimensional problems with compactly supported potentials were obtained by Ramm(see[6]–[7]).

For acoustic problems,the factorization method appeared in[8]for reconstructing anobstacle pointwise from knowledge of the normal far field integral operator F,and then was extended to reconstruct the support of 1−n(n denotes the index of refraction)for inverse medium scattering problem(see[9]).For an operator G which maps more general incident f i elds than plane waves into the scattering amplitude andthe basic idea of the factorization method is to solve the equation Gg=rz,and the test point z lies inside the obstacle or the support of 1−n is equivalent that the equation is solvable.The far field operator F has a factorization related to the operator G,and thus one can get that(F∗F)1/4and G have the same range.This range and as an application the boundary of obstacle or the support of 1−n can be characterized by the spectral data of the normal operator F. Grinberg extended this method to cover some kinds of boundary conditions which leads to non-normal operators for inverse obstacle scattering problems(see[10]).

In this paper we extend this method to the inverse scattering problem for Schrdinger equation to reconstruct the support of potential.Similar conclusions as the cases of inverse obstacle and medium scattering problems in acoustics can be obtained.We make the analysis carefully for the three-dimensioal case and state at last that this method can also be applied to the two-dimensional case.

Since the injectivity of the scattering amplitude opertor A is related to the existence of‘interior transmission eigenvalues’,we have to consider that there are‘how many’such eigenvalues.We can follow the argument of inverse medium scattering problem under further assumption on potential,but it is not enough to make a simple parallel discussion for the di ff erence of the operators in inverse medium and potential scattering cases.We resolve it by giving another assumption on potential so that the analytic Fredholm theorem can still be used to yield that there exists at most a countable number of eigenvalues k2.

This paper is organized as follows.In section 2 we introduce the direct scattering problem for Schrdinger equation with compactly supported potential and sketch the proof of its existence and uniqueness and the equivalence with the Lippmann-Schwinger integral equation.Both the concept of weak solution and the inverse potential scattering problem are introduced in Section 3 and we derive a factorization of the scattering amplitude operator A.We discuss the interior transmission problem in Section 4 and prove that A is injective if k2is not an interior transmission eigenvalue.In section 5,the main theorem of this paper is given to describe those points inside the support of the potential.In Section 6,we first explain that all of the results also hold for the two-dimensional case with possibly different constants,and then give two numerical experiments to illustrate the theorem.

2 The Direct Potential Scattering Problem

Let D⊂R3be a bounded domain with C2boundary∂D andR3D connected,and where C0,α(R3)denotes the Hlder continuous function space with Hlder index α.Letdenotes a plane wave inR3of directionˆθ∈S2where S2denotes the unit sphere inR3and k＞0 denotes the wave number.We consider the following scattering problem for Schrdinger equation:

where usdenotes the scattering wave.

Under the assumption(2.1)on q(x),it can be proved that there exists a unique solution for the direct scattering problem(2.2)–(2.4)by transforming the scattering problem into an equivalent integral equation.We sketch this approach since it is the basic tool in our further analysis.

We denote byΦ(x,y)the fundamental solution of the Helmholtz equation inR3,i.e.,

In fact,Φ(x,y)depends also on k and thus should be written asΦk(x,y).But,in this paper we omit the index k most of the time except for several places.The main properties of the volume potential are summarized in the following lemma.

Lemma 2.1We de fi ne the volume potentialωwith densityφ∈L2(D)by

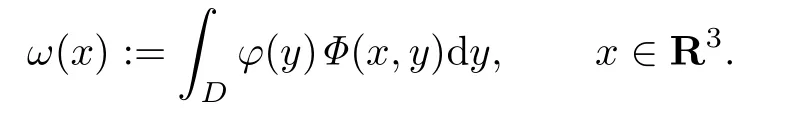
Then the following holds:

(a)ωis continuous inR3,analytic in the exteriorR3ofD,and satis fies the Helmholtz equation∆ω+k2ω=0inR3and the Sommerfeld radiation condition(2.4);

(b)Ifφ∈C(),thenω∈C1,α(D)for everyα∈(0,1);

(c)If evenφ∈C0,α(D)for someα∈(0,1],thenω∈C2,α(D)and∆ω+k2ω=−φinD. Furthemore,ifφ∈C0,α(D)is of compact support,thenω∈C2,α(R3),and∆ω+k2ω=−φinR3,whereφis extended by zero into the whole ofR3.

We can prove it according to the idea of[11]for the case of Newtonian potential.

A repeated application of this lemma and Theorem 5.6 in[12]shows that u∈C2(R3) is a solution of the scattering problem(2.2)–(2.4)if and only if u∈C()satis fies the Lippmann-Schwinger equation

Equation(2.5)is then written in short form as u+Tu=uior

Theorem 2.2Under the assumption(2.1)onq(x),there exists a unique solutionuof the scattering problem(2.2)–(2.4)or,equivalently,the Lippmann–Schwinger equation(2.5).

Proof.A similar proof to that of Theorems 5.4 and 5.5 of[12]shows that if q(x)satis fies the assumption(2.1),then the scattering problem(2.2)–(2.4)has at most one solution,i.e., the operator I+T is injective.Furthermore,T with weak singular kernal is compact,so the Riesz theorem([12],Theorem A.34)yields that I+T is also surjective,and thus there exists a unique solution of the equation(2.5)or,equivalently,the scattering problem(2.2)–(2.4).

We give the following lemma as preparation for later.

Lemma 2.3Ifq(x)satis fies(2.1),then the operatorI+Tis an isomorphism fromL2(D)onto itself.

Proof.Clearly,T is compact in C()and I+T is injective from C()onto itself,so I+T is also surjective by the Riesz theorem,which shows that I+T is an isomorphism from C()onto itself.

If there exists g∈L2(D)such that(I+T)g=0,then Tg∈C()by Lemma 2.1(a),and thus g∈C().We get g=0 for I+T is an isomorphism from C()onto itself,and thus I+T is injective from L2(D)onto itself.Since T is compact in L2(D),the Riesz theorem again yields that I+T is an isomorphism from L2(D)onto itself.This ends the proof.

3 The Factorization of the Scattering Amplitude Operator

The Lippmann-Schwinger equation(2.6)leads to a concept of weak solution as follows.

De fi nition 3.1Forh∈L2(D),the solutionv∈L2(D)of the integral equation

is called a weak solution of the direct potential scattering problem.

Under the assumption(2.1)on q(x),the scattering wave vsof the scattering problem (2.2)–(2.4)satis fies

As a special case,the scattering amplitude of the scattering problem(2.2)–(2.4)takes the form

Now we de fi ne the scattering amplitude operator A:L2(S2)→L2(S2)by

We note that Ag is the scattering amplitude pattern of the scattering problem(2.2)–(2.4) corresponding to the incident wave

If q(x)is of compact support,an argument analogous to the proof of Theorem 5.15 in[12] can show that the operator A is normal,and the scattering operator

Following the idea in[9],we de fi ne the operator G:L2(D)→ L2(S2)which maps h∈L2(D)into the scattering amplitude vaof the weak solution v of the problem(3.1),i.e.,

Instead of L2(D)we will work with the weighted space L2(D,q)which is de fi ned with respect to the inner product

In the following lemma we collect properties of the operators T and G in L2(D,q).

Lemma 3.2(a)The operatorTis well de fi ned and compact fromL2(D,q)into inself;

(b)The adjointT#ofTinL2(D,q)with respect toh·,·iqis given by

(c)BothI+TandI+T#are isomorphisms fromL2(D,q)onto itself;

(d)The operatorGis also well de fi ned and compact fromL2(D,q)intoL2(S2).

Proof.For a proof we refer to Lemma 2.3 in[9].

Theorem 3.3The scattering amplitude operator is

whereG#andT#are the adjoints ofGandTrespectively.

Proof.We de fi ne the auxiliary operator H:L2(S2)→L2(D,q)by

The function w=Hg is an entire solution of the Helmholtz equation

inR3and is called the Herglotz wavefunction.Observe that

and substituting this into A=−GH known by the de fi nition of A and G yields the assertion. This ends the proof.

For further reference we write(3.10)as

We see that the injectivity of the scattering amplitude opertor A is related to the existence of“interior transmission eigenvalues”.This investigation is the subject of the following section.

4 An Interior Transmission Problem

First,we formulate the interior transmission problem in spaces of smooth functions.

Given z∈D and α∈C, find v,w∈C2(D)∩C1(¯D)such that

We show at the end of this section that there exist at most a countable number of k∈R+for which the homogeneous problem corresponding to(4.1)–(4.2),i.e.,(4.1)–(4.2)with α=0, admits nontrivial solutions under more assumptions on q(x).

We de fi ne two closed subspaces of L2(D,q)as follows:

Here and in the following the closure,the orthogonal complement,and the adjoint are always taken with respect to the inner product h·,·iqin L2(D,q).

Lemma 4.1Ifq(x)satis fies the condition(2.1),then the following conclusions hold:

(a)BothI+TandI+T#are isomorphisms fromHqontoH1;

(b)The space{(Hg)|¯D:g∈L2(S2)}of Herglotz wavefunctions is dense inH1;

For a proof we refer the reader to the Lemma 3.1 in[9].

For our analysis it is necessary to introduce the concept of weak solutions of the interior transmission problem(4.1)–(4.2).

De fi nition 4.2Fixz∈Dandα∈R.

(a)A pair(v,w)∈L2(D,q)×L2(D,q)is called the weak solution of(4.1)–(4.2),if

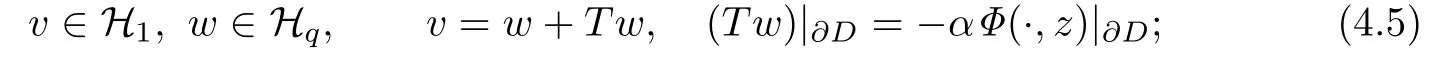
(b)k2is called an interior transmission eigenvalue if there exists a weak solution(v,w)(0,0)of the homogeneous interior transmission problem corresponding to(4.5),i.e.,(4.5)withα=0.

The equivalence of(4.1)–(4.2)and(4.5)is shown in the following lemma.

By Lax-Milgram theorem,for any φ∈L2(D,q)there exists a uniqueˆφ∈H with

We de fi ne P:L2(D,q)→H by Pφ=ˆφ and note that P is linear and bounded.

We transform the interior transmission problem into an equivalent equation in the following.

Lemma 4.4Fixz∈Dandα∈C.De fi ne

A similar proof as that of Lemma 3.4 in[9]can be given without essential di ff erence.

In order to show that A is injective,we prove the following lemma.

Lemma 4.5g∈L2(S2)is a solution of the homogeneous integral equationZ

Proof.Let g∈L2(S2)be a solution of(4.10)and de fi ne v(x)by(4.11).We observe that the left-hand side of(4.10)is a superposition of the scattering amplitude patterns.Therefore, the scattering amplitude waof the scattered wave wsthat corresponds to the incident wave v vanishes.The corresponding total solution w=ws+v satis fies the Schrdinger equation

By(4.10)and Rellich lemma(Lemma 5.2 in[12]),the scattered wave ws=w−v vanishes outside of.This yields that

This proves the first part of the lemma.

Now let v be of the form(4.11)and there exist w∈C2(D)∩C1()such that(v,w)solves the interior transmission problem(4.1)–(4.2)with α=0.Now we extend w(x)to the whole ofR3by setting w(x):=v(x)for x/∈D.Then w(x)∈C1(R3)and even w(x)∈C2(R3)by the similar proof to that of Lemma 5.12 in[12],and furthermore,w satis fies the Schrdinger equation

in the whole ofR3.w−v vanishes outside of D and obviously satis fies the Sommerfeld radiation condition.Therefore,w is the unique total solution corresponding to the incident wave v.The scattering amplitude waof the corresponding scattered wave w−v vanishes. As in the previous part,we see that wais a superposition

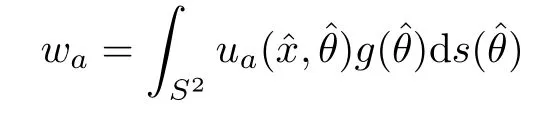
of total solution,and thus

for allˆx∈S2,i.e.,(4.10)holds.

Now we give the most important theorem of this section.

Theorem 4.6Ifk2is not an interior transmission eigenvalue,then for everyz∈Dandα∈C,there exists a unique weak solution of the interior transmission problem(4.5).In this case,Ais injective.

Proof.By Lemma 4.4,the equations(4.5)and(4.9)are equivalent.If k2is not an interior transmission eigenvalue,then w=0 for α=0,which means that I+PT is injective.Since P is bounded and T is compact we know that PT is compact.By the Riesz theorem again, I+PT is surjective too and(I+PT)−1is bounded.Thus there exists a unique solution for (4.5).If there exists g∈L2(S2)such that Ag=0,then(4.10)holds,and thus by Lemmas 4.5 and 4.3 there exists a unique weak solution of(4.5),i.e.,

where v is a Herglotz function,i.e.,

We know that v vanishes in the whole ofR3by the unique continuation principle of Helmholtz equation,and thus

which means that A is injective.This ends the proof.

Now we give further assumptions on q(x)as follows:

whereΦk0(x,y)denotes the fundamental solution of Helmholtz equation for k=k0.The following conclusion holds:

Theorem 4.7Ifq(x)satis fies the conditions(2.1),(4.12)and(4.13),then except for at most a countable number ofk,for everyk∈R+,k2is not an interior transmission eigenvalue.

Proof.If(v,w)solves the interior transmission problem(4.1)–(4.2)for α=0,then v∈H1, and thus Pv=0.For any u satisfying∆u+k2u=0 inR3,by Green’s second theorem and (4.2),

from which we know w∈H,and thus Pw=w.Rewrite(4.1)–(4.2)by Green’s representation theorem as follows:

Apply P to both sides of this equation to get

Obviously,both P and T are dependent of k,i.e.,(4.14),in fact,should be written as

If q(x)satis fies(4.12),the similar discussion to that of Section 8.6 in[15]yields that Pkand Tkare operator valued analytic functions in k.Pkis an orthogonal projection operator,and thus

if(4.13)is satis fi ed again,then

and thus the operator(I+Pk0Tk0)−1exists by the contraction mapping principle.We can conclude from the analytic Fredholm theorem that except for at most a countable number of k,for every k∈R+,the operator(I+PkTk)−1exists and thus w=0.By Green’s representation theorem and(4.2)again we know v=0.This ends the proof.

Remark 4.8Assume that D is contained in a sphere with radius a,V and M denote the volume of D and the upper bound of q(x)respectively.Now we give a condition to make (4.13)hold as follows:

Compared with(4.13),this condition can be checked much easily.

5 The Range of G

We denote by λj∈Cand ψj∈L2(S2)the eigenvalues and eigenfunctions,respectively,of A.Their existence is assured by the general spectral theory for compact normal operators. Furthermore,{ψj,j∈N}is a complete orthogonal system in L2(S2)provided A is injective.

Let

In the following we get the conclusions analogous to the case of inverse medium scattering problem.In order to prove that{φj:j∈N}forms a Riesz basis in

we want to apply the following lemma.

Lemma 5.1[8]LetHbe a complex Hilbert space,andK:H→Hbe linear and compact withImhKφ,φi0for allφ∈H,φ0.Let{φj:j∈N}be linearly independent and complete inH,i.e.,span{φj:j∈N}is dense inH.Let the elementsφjbe“orthogonal”in the sense that

wheresj∈Csatisfy the following conditions:There existsr＞0with

Theorem 5.2Assume thatk2is not an interior transmission eigenvalue.Then the functions{φj:j∈N}from(5.1)form a Riesz basis in

i.e.,every elementφ∈Hqhas a unique representation in the form

Proof.We wish to apply Lemma 5.1 to the space Hqand the operator

where Pqis the orthogonal projection operator from L2(D,q)to Hq.We only need to check the assumptions of Lemma 5.1 one by one,and for details we refer the reader to Theorem 4.2 of[9]for the case of inverse medium scattering problem.

Now we can give the main result of this section.

Theorem 5.3Assume thatk2is not an interior transmission eigenvalue,then we have

whereλj,ψjare the eigenvalues and eigenfunctions,respectively,ofA.HereG|H1is the restriction ofGto the closed subspaceH1ofL2(D,q).

We can prove it according to the idea of Theorem 4.3 of[9]without essential di ff erence.

As an application we give a simple characterization of the support of q(x)as follows.

Theorem 5.4Assume thatk2is not an interior transmission eigenvalue.De fi ne the functionrz∈L2(S2)by

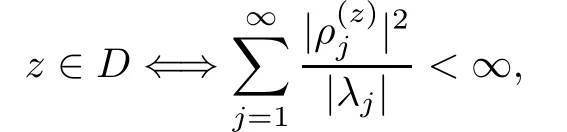
Thenz∈Dif and only ifrz∈R(G|H1),i.e.,by the previous theoremwhere∈Care the expansion coefficients ofrzwith respect toψj.

Once again,a similar proof to that of Theorem 4.4 of[9]can be given.

6 Numerical Implementation

Before we use the results of the previous section to visualize some examples we discuss brie fl y the di ff erence for two-dimensional scattering problems.Due to the asymptotic form of the fundamental solution of Helmholtz equation inR2taking the form

i.e.,S is unitary.This implies that the eigenvalues ofA lie on the circle of radiusand centreWe can now argue exactly as in the three-dimensional case,but for the operatorA instead of A.The phase shift,however,does not a ff ect the range of the scattering amplitude operator.Therefore,Theorem 5.4 remains true for this case.Though the factorization method can be applied to the two-dimensional case,we must remember that the uniqueness of the inverse scattering problem for this case has not been proved yet (see[16]and[17]).

Theorem 5.4 suggests a visualization of D in a very natural way.Let G be a domain containing the support of q(x).We choose a grid of test points P in G.Given k＞0,assume that we know the approximate values of the scattering amplitude ua(,),j,l=1,···,M, at equidistantly distributed directions

where θj=2πj/M.We call the discret form of the scattering amplitude operator as scattering amplitude matrix which is also denoted by A,i.e.,

Then we compute a singular value decomposition

of A.For each z in P we compute the expansion coefficients ofwith respect to the columns of V by

which is a matrix-vector multiplication

For each z we compute

By Theorem 5.4,the values of W(z)should be much smaller for z/∈D than for those lying within D.

We now consider the following two examples both assuming that

Example 1For x∈R2,let

where D denotes the unit circle inR2.

Example 2For x=(x1,x2)∈R2,let

where D denotes the domain enclosed by the curve obtained from being rotated π/3 anticlockwise around the point(0,0)for the‘kite-shaped’curve parametrized by

We solve the integral equation

to obtain the scattering amplitude matrix(ua(,)),where the solution u of the direct scattering problem is computed by the PML technique(see[18]).

For this two examples,we show the contour maps of W(z)in Figs 6.1 and 6.2 respectively. The broken line denotes the exact boundary of the support of the potential in each fi gure. Maybe the data of the scattering amplitude we used are not enough to describe the support of q(x)and,in addition,the error produced by solving the direct problem especially the integral equation must a ff ect the efficiency of reconstruction unavoidablly.

Fig.6.1 Example 1,Contour map of W(z)

Fig.6.2 Example 2,Contour map of W(z)

[1]Chadan,K.and Sabatier,P.C.,Inverse Problems in Quantum Scattering Theroy,2nd ed., Springer-Verlag,New York,1989.

[3]Ramm.A.G.,Inverse Problems,Springer,New York,2005.

[4]Aktosun,T.and Mee,C.V.D.,Solution of the inverse scattering problem for the threedimensional Schrdinger equation using a Fredholm integral equation,SIAM J.Math.Anal., 22(1991),717–731.

[5]Ramm,A.G.,Finding potential from the fixed-energy scattering data via D–N map,J.Inverse Ill-Posed Prob.,4(1996),145–152.

[6]Ramm,A.G.,Stability of the solutions to 3D inverse scattering problems with fixed-energy data,Milan J.Math.,70(2002),97–161.

[7]Ramm,A.G.,Fixed-energy inverse scattering,Nonlinear Anal.,69(2008),971–978.

[8]Kirsch,A.,Characterization of the shape of the scattering obstacle by the spectral data of the far- field operator,Inverse Problems,14(1998),1489-1512.

[9]Kirsch,A.,Factorization of the far- field operator for the inhomogeneous medium case and an application in inverse scattering theory,Inverse Problems,15(1999),413–429.

[10]Grinberg,N.I.,The operator factorization method in inverse obstacle scattering,Integral Equations Operator Theory,54(2006),333–348.

[11]Gilbarg,D.and Trudinger,N.S.,Elliptic Partial differential Equations of Second Order,2nd ed.,Springer,Berlin,1983.

[12]Kirsch,A.,An Introduction to the Mathematical Theory of Inverse Problems.Springer,Berlin, 1996.

[13]Ramm.A.G.,Completeness of the product of solutions to PDE and uniqueness theorems in inverse scattering,Inverse Problems,3(1987),L77–L82.

[14]Ramm,A.G.,Uniqueness theorems for multidimensional inverse problems with unbounded coefficients.J.Math.Anal.Appl.,136(1988),568–574.

[15]Colton,D.and Kress,R.,Inverse Acoustic and Electromagnetic Scattering Theory,Springer, New York,1992.

[16]Isakov,V.and Sun,Z.,The inverse scattering at fixed energies in two dimensions,Indiana Univ.Math.J.,44(1995),883—896.

[17]Serov,V.S.,Some inverse scattering problems for two-dimensional Schrdinger operators,in: Proceedings of the 5th international conference on inverse problems in engineering:theory and practice,Cambrige,UK,11-15th,July,2005.

[18]Chen,Z.M.and Liu,X.Z.,An adaptive perfectly matched layer technique for time-harmonic scattering problems.SIAM J.Numer.Anal.,43(2005),645–671.

35R30,65K05,81U40

A

1674-5647(2010)04-0321-16

date:Dec.26,2008.

The Major State Basic Research Development Program Grant(2005CB321701)and the Heilongjiang Education Committee Grant(11551364)of China.