数字电位器的数学模型及测试技术

李 玮,沙占友,于健骐,李永伟

(1.河北科技大学电气信息学院,河北石家庄 050018;2.河北科技大学信息科学与工程学院,河北石家庄 050018;3.中国环境管理干部学院信息工程系,河北秦皇岛 066004)

数字电位器的数学模型及测试技术

李 玮1,沙占友2,于健骐3,李永伟1

(1.河北科技大学电气信息学院,河北石家庄 050018;2.河北科技大学信息科学与工程学院,河北石家庄 050018;3.中国环境管理干部学院信息工程系,河北秦皇岛 066004)

数字电位器是一种颇具发展前景的新型电子器件,可在许多领域取代传统的机械电位器。单片机通过接口电路对数字电位器进行编程,即可构成可编程增益放大器、可编程滤波器等各种可编程模拟器件,实现“把模拟器件放到总线上”(即微控制器通过总线来控制系统中的模拟功能块)这一全新的设计理念。首先建立了数字电位器(DCP)的拓扑结构,不仅从本质上表述了数字电位器的调节特性及内部2个电阻变量的依存关系,为深入分析数字电位器在模拟电路中的工作特性提供了便利条件。阐述了数字电位器的测试电路原理、测试方法、测试数据及注意事项。

数字电位器;数学模型;测试电路;非线性误差

数字电位器(digital potentiometer)亦称数控电阻器(digitally controlled potentiometers),可简称为DCP。它是采用CMOS工艺制成的数字-模拟混合信号处理集成电路,可广泛用于仪器仪表、计算机及通信设备、家用电器、医疗保健产品、工业控制等领域。实际上,任何需要用电阻来进行参数调整、校准或控制的场合,都可使用数字电位器构成可编程模拟电路[1]。

1 数字电位器的数学模型

数字电位器(DCP)的数学模型如图1所示。其中,图1a)为数字电位器的拓扑结构,它从本质上反映了数字电位器的调节特性及内部2个电阻变量的依存关系。图1b)为数字电位器的等效电路,它等效于由2个可调电阻串联而成、能同步调节的电阻。假定数字电位器的总抽头数为n,所用抽头序号为n1,数字电位器滑动端的比例位置为k,则有关系式:

式中,0≤k≤1。因此,数字电位器的总电阻R就被滑动端划分成2个互补电阻:kR,(1-k)R。二者呈互补关系,具体电阻值取决于由输入代码所确定的滑动端的位置[2]。

图1 数字电位器的数学模型Fig.1 Mathematicalmodel of digital potentiometer

图1c)为对数字电位器集成电路进行计算机仿真的SPICE(sim ulation p rogram w ith integrated circuit emphasis)模型。图中,R为数字电位器的总电阻,RW为滑动端电阻,CW为滑动端对地的电容,CH和CL分别为数字电位器高端、低端对地的电容。通常,R=1 kΩ～1 MΩ,RW=40～400Ω,CW=3～80 p F,CH,CL=7.5～20 p F。通常 ,CW>CH,CL[3]。

由上可归纳出数字电位器具有的特点:1)数字电位器可等效于三端可编程电阻,互补电阻kR和(1-k)R是输入代码的函数;2)数字电位器的输出量是电阻值或电阻比率,可视为电阻式数/模转换器(RDAC);3)数字电位器的输出电阻可转换成电压或电流输出[4]。

2 数字电位器的测试电路及测试方法

在介绍数字电位器测试电路及测试方法中,被测参数包括积分非线性误差(INL)和微分非线性误差(DNL)、滑动端电阻(RW)和滑动端电容(CW)。

2.1 测试数字电位器的非线性误差

非线性是指数字电位器的输出与输入之间不呈线性关系。数字电位器的非线性有2种:一种为积分非线性(integral nonlinearity,INL),另一种为微分非线性(differential nonlinearity,DNL)。积分非线性误差(INL error,简称INL),是指扣除失调误差和增益误差后,实际传递函数曲线与理想传递函数曲线的最大偏差,其单位用LSB(least significant bit,最低有效位)来表示;当 INL>0时,表示实际电阻值比理想电阻值高;当INL<0时,表示实际电阻值比理想电阻值低。微分非线性误差(DNL error,简称DNL),是指实际代码宽度与理想代码(1LSB)宽度的误差;这里讲的代码宽度,就是1个步长所对应的十进制编码。

数字电位器的积分非线性误差曲线和微分非线性误差曲线分别如图2a)、图2b)所示。

由图可见,积分非线性误差是从整个传递函数曲线的角度来反映非线性误差大小的,它具有“积分”特性;微分非线性误差则是从传递函数曲线的微观角度(1个步长所对应的十进制编码)来反映非线性误差大小,具有“微分”特性。这是二者的区别。

数字电位器在分压器模式下,积分非线性误差和微分非线性误差的测试电路如图3a)所示。

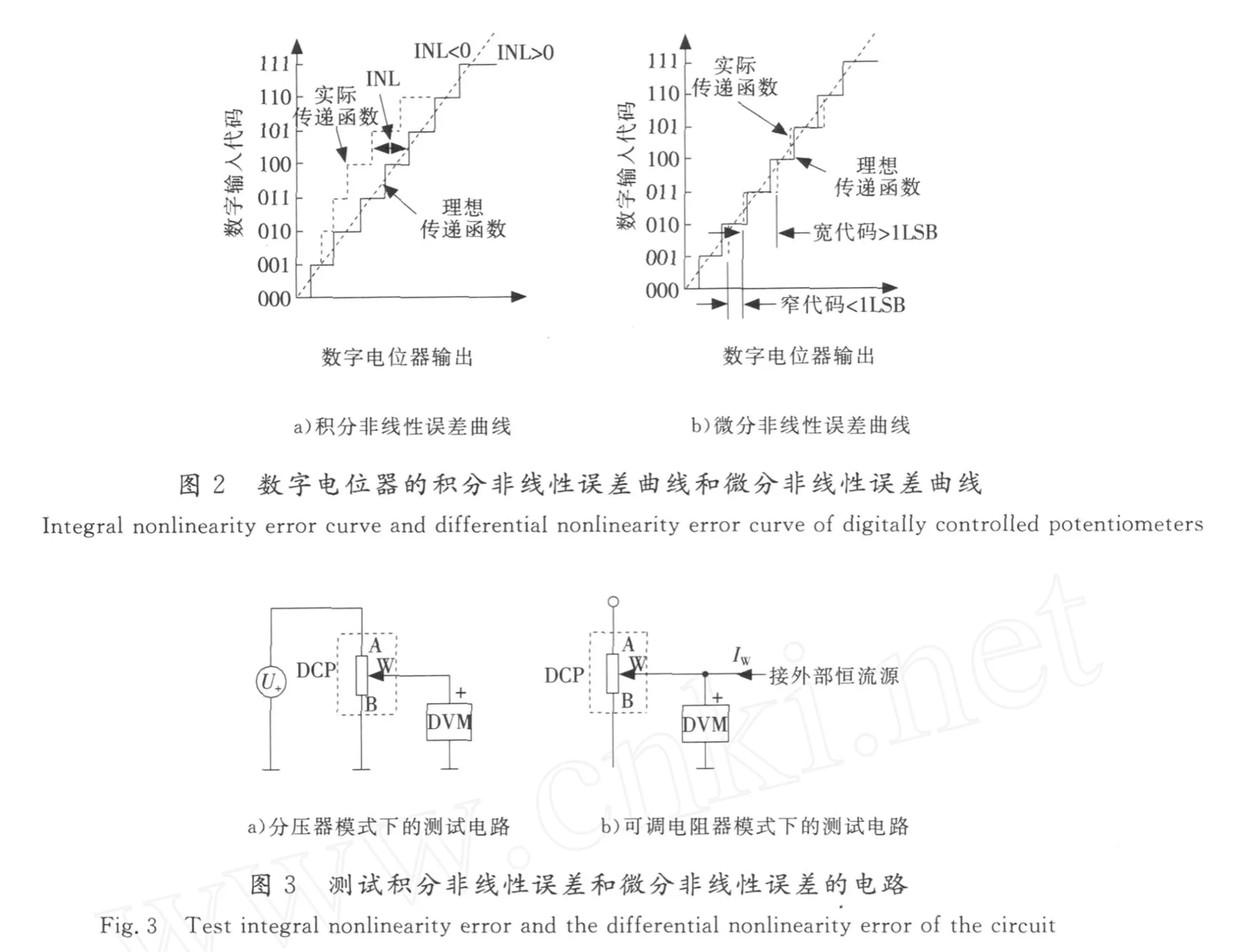
图中的U+为高阻抗电压源,并且U+=UDD。U+经过数字电位器分压后,接高输入阻抗的数字电压表(DVM)。由于DVM的读数代表实际测量值,DCP的滑动端编码代表理想值,因此只要将滑动端位置从B端滑动到A端,即可测出积分非线性误差。若只将滑动端移动1个步长,则可测出微分非线性误差。例如,实测MCP41XXX/42XXX系列数字电位器在分压器模式下,积分非线性误差、微分非线性误差均为±1/4LSB。

在可调电阻器模式下,积分非线性误差和微分非线性误差的测试电路如图3b)所示。将数字电位器的A端悬空,由外部恒流源提供滑动端电流IW。IW流过W,B端所形成的压降,可用数字电压表测量,具体测量步骤同上。MCP41XXX/42XXX系列数字电位器在可调电阻器模式下,实测的积分非线性误差、微分非线性误差分别为±1/4LSB(典型值),最大值为±1LSB。

2.2 测试数字电位器的滑动端电阻

滑动端电阻是指数字电位器内部模拟开关(亦称传输门)的导通电阻。该电阻值与数字电位器的内部电路结构有关,通常为几十欧姆至一百几十欧姆。MCP41XXX/42XXX系列的滑动端电阻测试条件为UDD=+5.5 V,IW=1 m A,16进制编码为00H(所对应的十进制编码为0)。测试数字电位器滑动端电阻的电路如图4所示。

E1为0.1 V直流电源,给数字电位器的W,B端提供电流。E2为可调直流电源,调节范围是0～UDD。当16进制编码为00H时,滑动端位于B端,此时W,B两端之间的电阻就等于滑动端电阻RW。滑动端电流IW可用电流表测出。计算滑动端电阻的公式为

测量时需要注意2点:第一,E1不得超过0.1 V,以免因IW过大而损坏滑动端,通常选1 m A为宜;第二,滑动端电阻与工作电压有关,实际测量时B端还应接一个直流工作电压,用可调直流电源E2代替,但E2不得超过数字电位器的电源电压范围,一般应低于5.5 V。

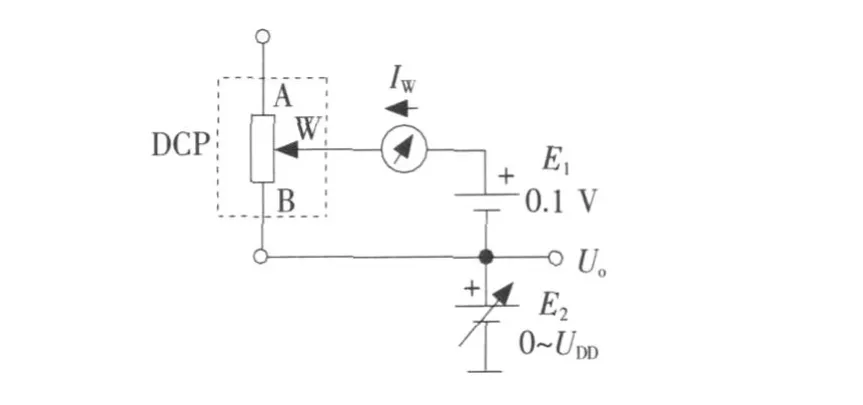
图4 测试数字电位器滑动端电阻的电路Fig.4 Circuit for testing digital potentiometer w iper resistance

2.3 测试数字电位器的滑动端电容

测试数字电位器滑动端电容的电路见图5。

虽然微胖，但周岱翰的身体极好，因为他精通食疗之法，其著作《中医肿瘤食疗学》中介绍的食材和烹调方法多是他实践的成果。

UI为交流信号源,R1为输入电阻。数字电位器(DCP)工作在可调电阻器模式,接在运放的反相输入端与输出端之间,起负反馈作用。设数字电位器的总电阻值为R,预先将滑动端W移动到中央位置,以256抽头数字电位器为例,其中央位置所对应的16进制编码为80H(折合十进制编码为128),此时数字电位器的实际电阻值为R/2。W端与B端之间的电容就是滑动端电容CW。CW与R/2相并联,使反馈电路具有一定的容抗性质。CW的容量非常小(例如,MCP41XXX/42XXX系列的典型值仅为5.6 p F),在低频(几千赫兹以下)时CW的容抗为无穷大,可忽略其并联作用。但在高频情况下,CW在反馈电路中的容抗效应就不容忽略,CW与R/2并联后会使反馈电路的总阻抗显著降低。只要用示波器或高频数字电压表分别测量出运放在输入低频、高频信号时的输出电压,即可计算出CW值。下面分析该电路的测量原理[5]。

设CW的容抗为XC,XC与R/2并联后的阻抗为Z,输入低频信号UI时(f=10 kHz),运放的输出电压为Uo,输入高频信号(f=1 M Hz)时,运放的输出电压为U′o。关系式如下:

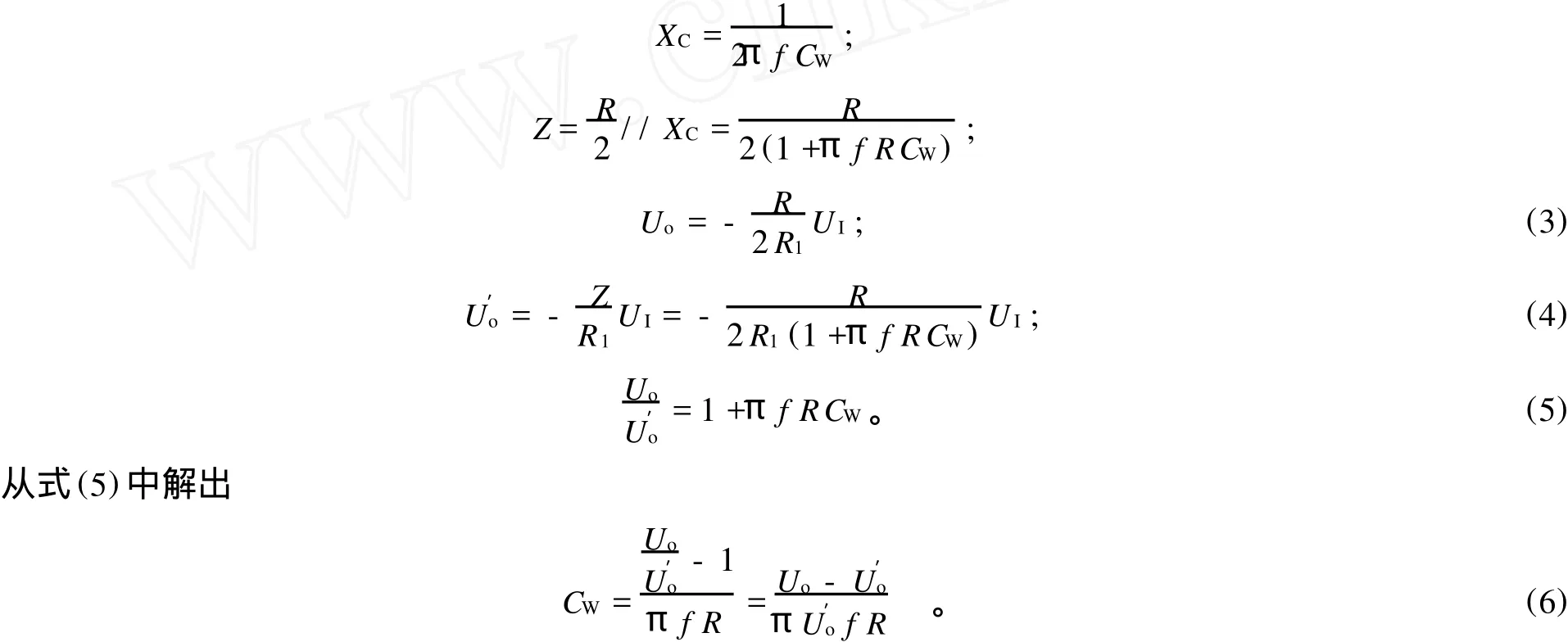
图5 测试数字电位器滑动端电容的电路Fig.5 Circuit for testing digital potentiometer w iper capacitance

举例说明,已知数字电位器MCP41100的总电阻R=100 kΩ,MCP41100和运放的电源电压取+5 V,输入高频信号频率f=1 M Hz。在输入信号幅度不变的情况下,实测Uo=1.5 V,U′o=1.0 V,即Uo/U′o=1.5。代入式(6)中得到CW=6.3 p F,与典型值5.6 p F很接近。

需要说明几点:

1)MCP41XXX/42XXX系列的-3 dB带宽仅为145 k Hz(典型值),而输入高频信号频率选1 M Hz,目的是为了使CW的容抗效应更加突出;

3)所采用的运放必须具有满幅电源电压输出特性(即“轨对轨”),例如MCP601型低功耗单运放,其电源电压范围是+2.7～+5.5 V,恰好与MCP41100相同。

3 结 语

掌握数字电位器的拓扑结构、配置模式及测试方法,对实现数字电位器的优化设计具有重要意义。单片机通过接口电路对数字电位器进行编程,即可构成可编程增益放大器、可编程滤波器等各种可编程模拟器件,实现微控制器通过总线来控制系统中的模拟功能块这一全新的设计理念。

[1]沙占友.数字化测量技术与应用[M].北京:机械工业出版社,2004.

[2]吴晓波,方志刚.一种精密集成温度传感器的研制与应用[J].仪表技术与传感器(Instrument Technique and Sensor),2007(1):13-16.

[3]陈巧玲.一种简易数字式信号测试仪的设计[J].漳州师范学院学报(Journal of Zhangzhou Teachers College),2004(6):2-5.

[4]薛同泽,沙占友,张永昌.开关电源的节能新技术[J].河北科技大学学报(Journal of Hebei University of Science and Technology),2003,24(3):54-58.

[5]李庆恒,沙占友.基于以太网接口的电源变换器的设计[J].河北科技大学学报(Journal of Hebei University of Science and Technology),2006,27(1):74-77.

Topology and test technology of digitally controlled potentiometers

L IWei1,SHA Zhan-you2,YU Jian-qi3,L I Yong-w ei1
(1.College of Electrical Engineering and Information Science,Hebei University of Science and Technology,Shijiazhuang Hebei 050018,China;2.College of Info rmation Science and Engineering,Hebei University of Science and Technology,Shijiazhuang Hebei 050018,China;3.Info rmation Engineering Department,Environmental Management College of China,Qinhuangdao Hebei 066004,China)

The digitally controlled potentiometers(DCP)is a new type of electronic device,w hich has good development p rospect.And the DCP can rep lace the traditionalmechanical potentiometer inmany fields.Through controlling the DCP by MCU,a p rogrammable gain amp lifier,a p rogrammable filter and other p rogrammable analogy devices can be composed.Through this method,the new design technology of“put the analogy deviceonto the bus”,w hich means the MCU controls the analogymodules through bus,can be realized.Firstly the topology of the DCP is set up,w hich can indicate the adjustable characters and dependence relationship between the internal two resisters.The topology of the DCP also p rovides conditions for analyzing the operation charactersof the DCP in the analogy circuit.Finally the test circuit’s p rincip le,testmethods,test data and note item s of the DCP are expatiated upon.

digitally controlled potentiometers;mathemmaticalmodel;test circuit;nonlinear erro r

TP212

A

1008-1542(2010)02-0116-04

2009-08-10;

2009-10-27;责任编辑:李 穆

李 玮(1963-),女,河北石家庄人,副教授,硕士,主要从事检测技术与自动控制方面的研究。